Примеры решения задач

Пример 8. Груз массойm= 45кг вращается на канатеl = 5,0 мв горизонтальной плоскости, совершаяn= 16 об/мин. Какой угол с вертикалью образует канат и какова сила его натяжения?

Решение:

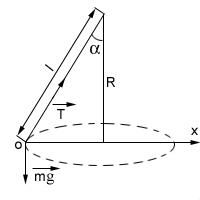
Рисунок 11 – Пример 8

На груз действует сила тяжести и сила натяжения каната. Выбираем начало координат в произвольной точке нахождения груза, в данном случае в точкеОдля наглядности чертежа (рисунок 11).

Уравнение движения по второму закону Ньютона записывается в виде

+=; (48)

так как движение по окружности происходит с постоянной скоростью (по модулю), то полное ускорение тела - нормальное ускорение, направленное к центру окружности радиуса R.

(49)

Ось Хвыбрана по направлению скорости. Проектируя векторы, входящие в уравнение (2) на оси, имеем систему уравнений

Tsin  = m4² n² R ;

Tcos  = mg = 0.(50)

Из рисунка 11 следует R = l sin.Решая уравнение (50) совместно, имеем

T= m4 n² l,

 = arccos .

Подставляя числовые значения в единицах СИ и выполнив вычисления, находим

T= 0,63 кН,

cos  = 0,71 ,

 = 45⁰.

Пример 9. С какой максимальной скоростью может ехать мотоциклист по горизонтальной плоскости, описывая дугу радиусаr = 90 м, если коэффициент трения колёс о почву = 0,4(рисунок 12).На какой угол от вертикали должен отклониться мотоциклист при скорости = 15 м/с?

Решение:

Система мотоциклист и машина рассматриваются как единое точечное твёрдое тело.

При движении по кругу мотоциклист будет обязательно отклоняться от вертикального положения, и движение его в принципе, не будет поступательным, так как скорости различных точек системы отличны друг от друга. Мы рассматриваем скорость центра масс и его нормальное ускорение.

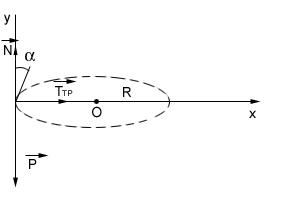
Рисунок 12 – Пример 9

На мотоциклиста действуют следующие силы:

1. сила тяжести ;

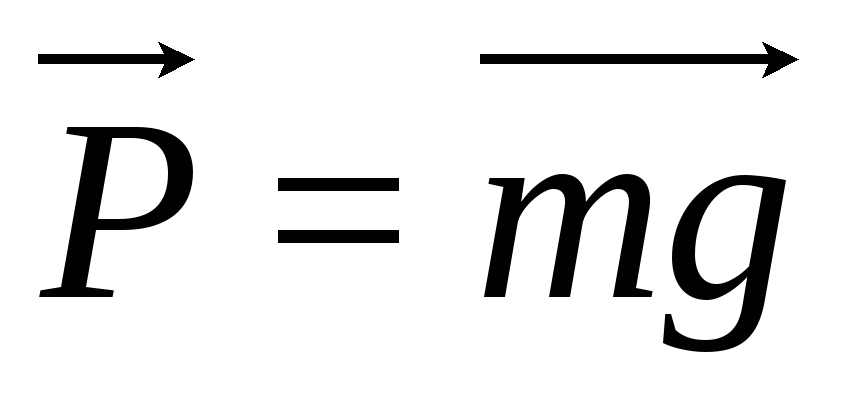2. сила нормальной реакции ;

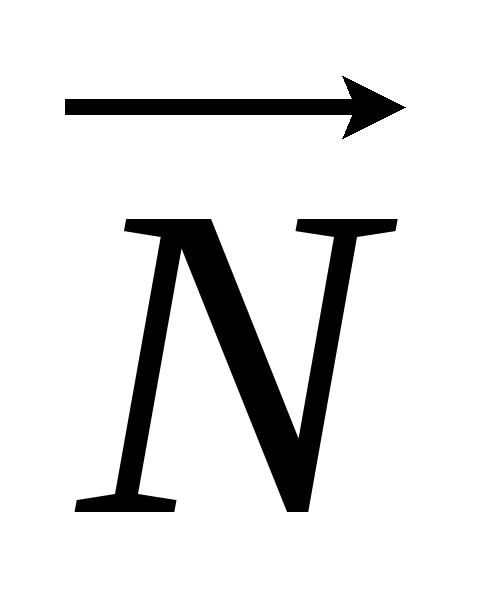3. сила трения ;

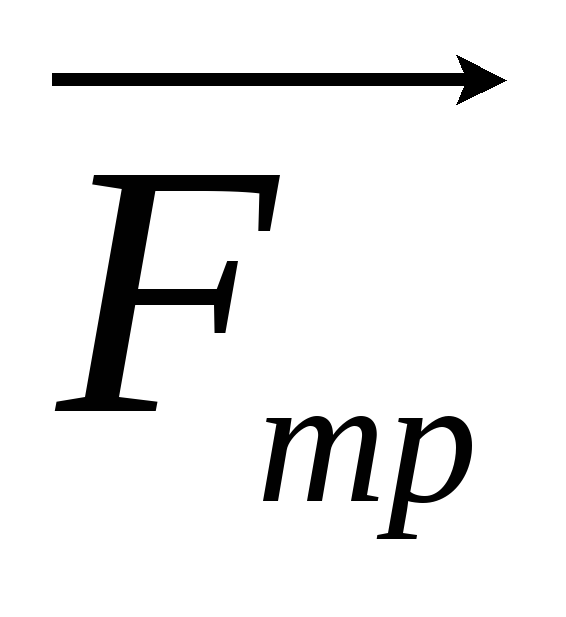4. сила тяги, направленная по касательной к траектории;

5. сила трения покоя, направленная к центру описываемой траектории.

Так как линейная скорость мотоциклиста постоянна, то сумма проекций всех сил на направление касательной равна нулю. Ускорение центра масс направлено к центру и равно .

Рассмотрим уравнение движения по второму закону Ньютона:

++=(51)

Указанные силы приложены в разных точках, вследствие чего на мотоциклиста действует еще вращательный момент. Этот момент нулевой, если результирующая сила нормального давления и силы трения пройдут через центр масс, так как

(52)

Но в радиальном направлении мотоциклист не имеет скорости, значит:

(53)

Проектируем векторы, входящие в уравнение (51) на оси:

m=,

0 = N-P

Совместное решение скалярных уравнений (53) приводит к выражению

= kN= m= kP = kmg ;

m = kmg ;

= kgR ;

= 19 м/с.

При скорости имеем

= m,

.

При :.

Пример 10. Гиря, положенная на верхний конец стальной пружины, сжимает ее нах₀=1,0 мм. На сколько сожмет пружину эта же гиря, брошенная вертикально вниз с высотыh=0,2 мсо скоростью = 1,0 м/с(рисунок 13)

Решение:

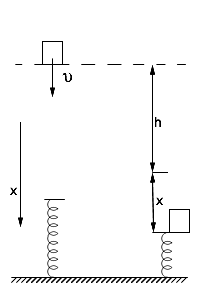
Рисунок 13 – Пример 10

Искомая величина Xдеформации пружины определяет потенциальную энергию тела, так как энергия упругого деформированного тела определяется по формуле

,(54)

где k– коэффициент упругости, определяемый отношением упругой силы и величиныхупругой деформации.

Для решения воспользуемся законом сохранения энергии. Рассмотрим систему Земля – гиря – пружина, так как при движении и сжатии пружины трения нет, то механическая энергия этой системы сохраняется.

Подсчитаем энергию системы в начальном и конечном положениях. За нулевой уровень отсчета выберем самое нижнее положение гири, соответствующее сжатой пружине.

В начальном положении энергия системы Wскладывается из потенциальной и кинетической энергии гири:

(55)

В конечном положении у гири не будет кинетической энергии, зато сжатая пружина обладает энергией упругой деформации:

, (56)

где k = .Приравнивая по закону сохранения энергии правые части (55) и (56), получим

. (57)

Решение (57) находят в виде

.

Отрицательный корень x<0соответствует растяжению пружины, поэтому отбрасывается.х=810^-2; M=8см.

Пример 11. На рельсах в горизонтальной плоскости стоит платформа с песком общей массойm = 510³ кг. В платформу попадает снаряд массойm=5кг, летящий со скоростью = 400 м/с.Снаряд летит под углом = 36к горизонту. Найти скорость платформы, если снаряд застрял в песке (рисунок 14).

Решение:

Эта задача не может быть решена непосредственно с помощью законов Ньютона. Платформа приобретает скорость в результате взаимодействия со снарядом. Однако закон этого взаимодействия со временем не известен. На систему платформа-снаряд действуют силы: 1) сила тяжести; 2) сила нормальной реакции; 3) сила трения; 4) сила взаимодействия платформы и снаряда.

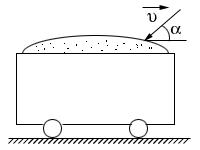
Рисунок 14 – Пример 11

Вследствие негоризонтального направления скорости снаряда сила нормальной реакции, действующая на платформу меняется. Поэтому закон сохранения количества движения к данной системе не применим.

Если пренебречь силой трения (по сравнению с силой взаимодействия платформы и снаряда), сумма проекций внешних сил на горизонтальное направление равно 0, так как силу взаимодействия снаряд-платформа считаем внутренней для данной системы.

Значит, проекция вектора полного импульса системы на горизонтальное направление остается постоянной:

k_1x = k_2x, (58)

где k_1x – проекция вектора импульса системы до взаимодействия ;

k_2x– после взаимодействия.

Тогда k_1x = ,

так как =;

k_2x = (m+M)u.

С учетом (58) имеем (m+M)u = ;

u = м/с.

Пример 12. Снаряд, летевший горизонтально со скоростью =100 м/с, разрывается на две части на высотеН=40 м. Одна часть падает через времяt=1cна землю точно под местом взрыва. Определить величину и направление скорости второй части снаряда сразу после взрыва (рисунок12).

Решение:

Снаряд и два его осколка считаем замкнутой системой. Значит, полный вектор импульса системы за время взрыва не меняется (из-за кратковременности взрыва и огромных сил, возникающих при этом), то есть

= (59)

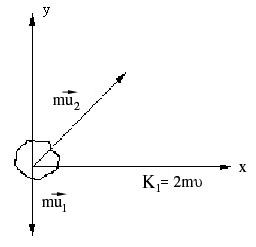
Рисунок 15 – Пример 12

До взрыва вектор направлен горизонтально. После взрыва полный вектор импульсаравен сумме векторов импульсов двух осколков. Введя координатные оси, имеем

= 2m ;

= +.

По рисунку видно:

Отсюда u₂ = .

Для первого осколка имеем Н = u₁t + ;

u₁ = 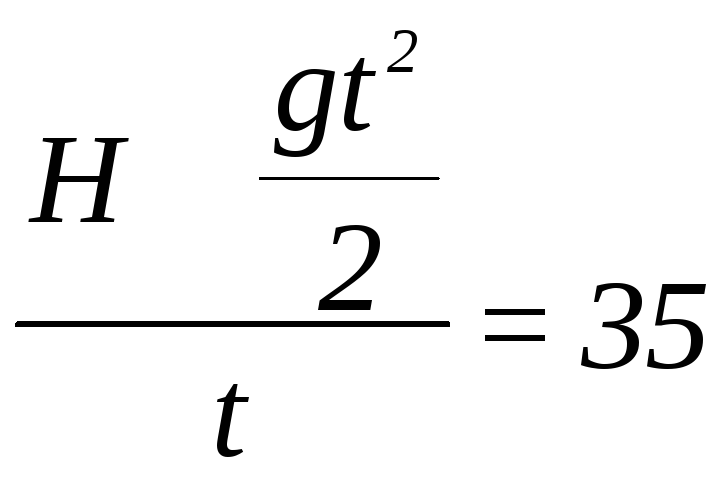м/с.

Тогда u₂ = 202 м/с.

Вектор направлен к горизонту под углом:

;

=10.

Пример 13. При упругом ударе нейтрона о ядро углерода он движется после удара в направлении, перпендикулярном начальному. Считая, что массаМядра углерода вn = 12 раз больше массыmнейтрона, определить, во сколько раз уменьшится энергия нейтрона в результате удара.

Решение:

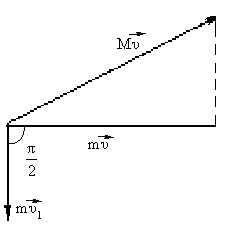
Рисунок 16 – Пример 13

Если скорость нейтрона до удара ,- после удара,- скорость ядра углерода после удара (до удара – нуль).

В результате упругого удара импульс и энергия, которыми до удара обладает нейтрон, распределяются между двумя частицами.

При этом по законам сохранения импульса и энергии имеем

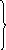(60)

По условию задачи требуется найти

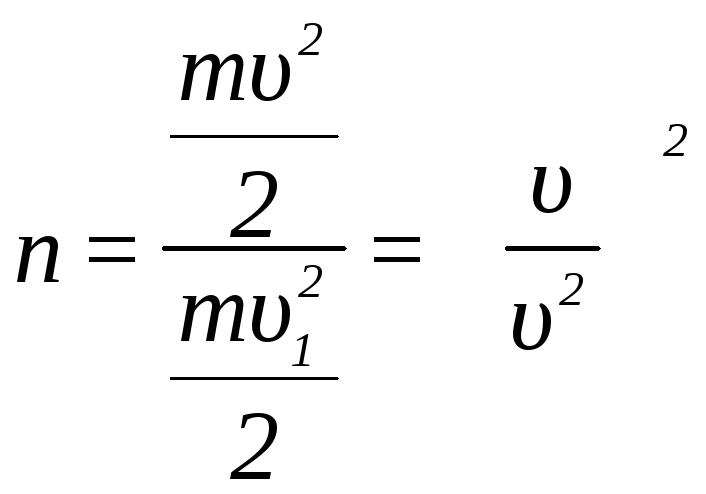
Принимаем метод проекции с учётом того, что угол между векторами иравен.

Из треугольников импульсов имеем

. (61)

Кроме того, = 12по условию задачи.

Разделим почленно выражение закона сохранения энергии на m, а уравнение (2) наm²:

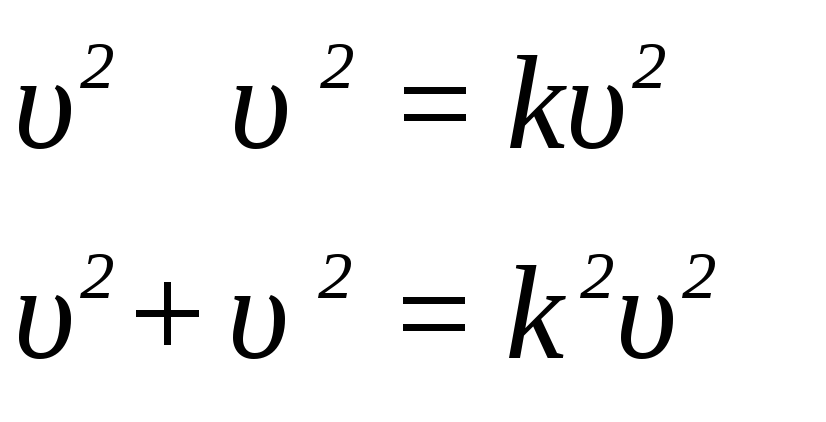
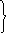(62)

Исключая в этой системе уравнений, получим

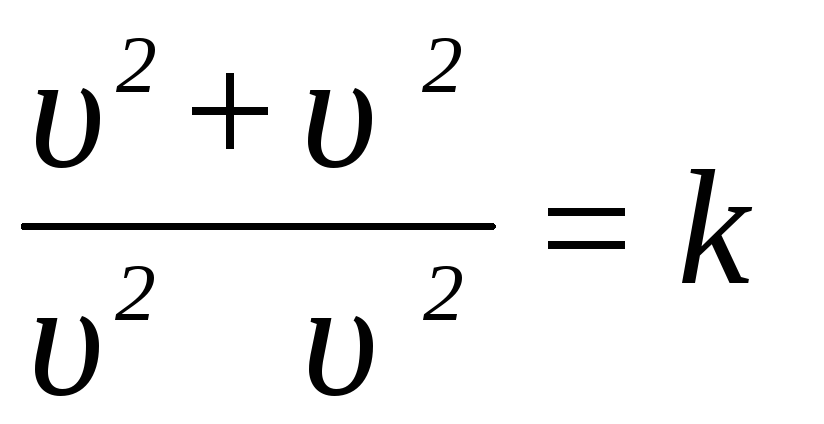. (63)

Числитель и знаменатель (63) делим почленно на и находим

,

откуда .

Пример 14. Шарик массойm = 0,1 кг, падая с некоторой высоты, ударяется о наклонную плоскость и упруго отскакивает от нее без потери скорости. Угол наклона плоскости к горизонту = 30.За время удара плоскость получает импульс силы = 1,73Нс. Какое времяtпройдет от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории?

Решение:

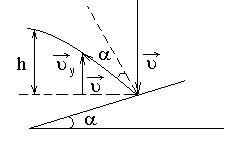
Рисунок 17 – Пример 14

По закону сохранения импульса:

=,

где =сos - (-сos);

= сos (+);

==;

отсюда = 2сos.

Тогда =2mсos. (64)

И

-

з рисунка видно, что =sin-gt = сos2 - gt;

=0в верхней точке, следовательно:

сos2 = gt,

откуда t = .

Из (64) найдем =

тогда t =

t = 0,51 c.

Пример 15. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30и = 45.Гири1и2одинаковой массыm₁ = m₂ = 1 кгсоединены нитью и перекинуты через блок. Коэффициенты трения гирьk₁ = k₂ =0,1. Найти ускорениеa, с которым движутся гири, и силу натяжения нитиТ.

Решение:

Рисунок 18 – Пример 15

Пусть при данном значении kгири скользят. С учетом силы трения уравнение второго закона Ньютона в проекциях на направление их движения запишется в виде

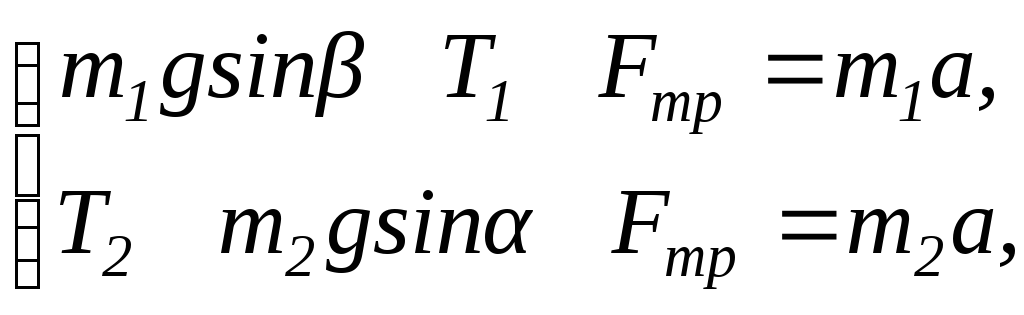
или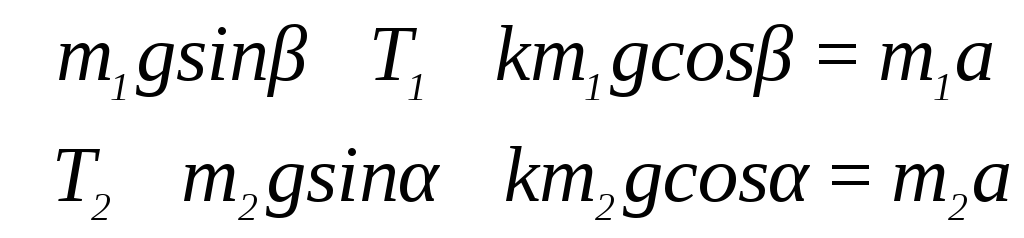

Так как Т₁ = Т₂, то сложив (65) и (66), получим

;

,

откуда a = g . (67)

Из (66) найдем Т₂ = ++,

подставив в это выражение (67), получим

Т₂ =  +;

Т₂ = ;

Т₂ =;

Т₂ =;

Т₂ =

Подставляя числовые данные, получим

Т₁ = Т₂ = 6Н, а = 0,244 м/с².

Пример 16. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пулиm₁=5г, масса шараm₂=0,5 кг. Скорость пули₁=500 м/с. При каком предельном расстоянииlот центра шара до точки подвеса стержня шар от удара пули поднимется до верхней точки окружности?

Решение:

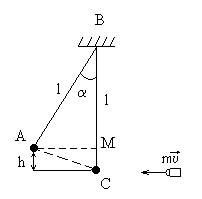
Рисунок 19 – Пример 16

Запишем закон сохранения импульса и закон сохранения энергии для данной системы:

m₁₁= (m₁+m₂)₂(68)

(m₁+m₂)gh, (69)

где ₂ – скорость шара с пулей после удара.

Высота, на которую поднимается шар, h = 2l.

Из (69) 2gl,откудаl = .

Из (68) ₂= ,

тогда l= ;

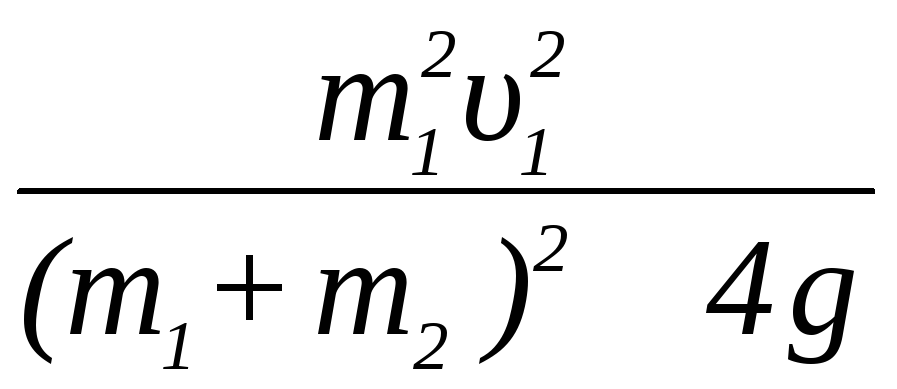l = 0,64 м.

Содержание

С.

Физические основы механики 2

Кинематика 3

Ускорение 6

Движущиеся системы отсчета 9

Примеры решения задач по кинематике 10

Движение твердого тела 13

Примеры решения задач на вращательное движение твердого тела 16

Законы динамики 23

Значение и содержание законов сохранения 28

Закон сохранения энергии 30