Ускорение

При прямолинейном движении быстрота изменения величины скорости характеризуется ускорениема– изменением величины скорости за единицу времени.

В случае произвольного криволинейного движения вектор скорости может меняться по величине и по направлению.

Быстрота изменения вектора скорости в этом случае характеризуется вектором ускорения , расчленяемым на две составляющие, определяющие в отдельности быстроту изменения скорости по величине и быстроту изменения скорости по направлению.

Н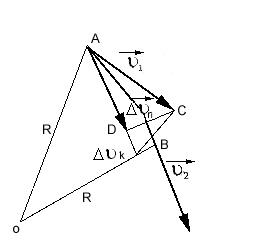а рисунке 3 изображен отрезок траектории между двумя соседними бесконечно близкими точкамиАиВ. Скорости в этих точкахинаправлены по касательным к траектории в этих точках и отличаются по величине и по направлению.

Рисунок 3

Причем рассматриваем случаи, когда скорость в точке Вбольше по величине. Перенесем векторпараллельно самому себе в точкуА. Соединяя конец векторас концом вектора, получаем вектор=-.

Это геометрическое приращение вектора за время.

Тогда а_ср=. Это отношение называется средним ускорением. Переходя к пределу, выражают мгновенное ускорение:

а==. (7)

Откладывая на перенесенном векторе отрезок, численно равный длине вектора, видим, что векторможет быть представлен как геометрическая сумма двух векторов:

=-, (8)

где - численно равен изменению величины скорости за:=-.

Если величина скорости не меняется, то =0,=0.

характеризует изменение направления вектора скоростиза время. Он направлен в сторону вогнутости траектории. В выражение (7) поставим значениеиз (8):

==+=+. (9)

Вектор =также направлен по касательной к траектории, а модуль этого вектора равена_k=- тангенциальное ускорение.

Для определения второй составляющей в уравнении (9) восстановим перпендикуляры к касательным в точках АиВдо пересечения их в точкеО. Малая дугаS = АВесть отрезок окружности с центром в точкеОи радиусомОА=ОВ=R.

Треугольники АОВиСАDподобны, т.к. имеют одинаковые углы при вершине (углы со взаимно перпендикулярными сторонами).

Тогда или =,=. Делим на:= .

Переходя к пределу :

а_n=== =(10)

Таким образом, численное значение нормального ускорения в данной точке равно квадрату скорости, деленному на радиус кривизны в той же точке:

а_n=

Вектор ускорения есть векторная сумма нормального и тангенсального ускорения (уравнение 9).

==+=+.

Движущиеся системы отсчета

Рассмотрим движение материальной точки относительно системы отсчета, которая сама движется равномерно и прямолинейно относительно другой, покоящейся, например, относительно Земли. Систему отсчета, связанную с Землей, условно назовем «неподвижной», и скорость относительно этой неподвижной системы назовем «абсолютной» скоростью. Термин «абсолютный» взят в кавычки, поскольку в мире нет абсолютного покоя и абсолютного движения.

Скорость тела относительно движущейся системы отсчета назовем относительной. Отсчет времени полагаем в обеих системах одинаковым. Хотя такое предположение и подвергнуто критике А. Эйнштейном, но в рамках классической механики применительно к макротелам, движущимся со скоростями малыми по сравнению со скоростью света, его можно считать справедливым.

Если за промежуток времени перемещение материальной точки относительно подвижной системы, то за это же время сама система сместилась относительно «неподвижной» на расстояние.

Тогда перемещение материальной точки относительно «неподвижной» системы=+, а средняя «абсолютная» скорость= = + приt  0

=+, (11)

где - «переносная» скорость.

Итак, абсолютная скорость равна геометрической сумме относительной и переносной скоростей.