6.4. Качество обслуживания и основные показатели работы маркера.
Как изменится качество обслуживания и основные показатели работы маркера, если:
А) Он будет работать в 2 раза быстрее:
При работе маркера в 2 раза быстрее время обслуживания одного вызова уменьшится в 2 раза:
Нагрузка на маркер блока уменьшится в 2 раза:
Время занятия станет:
По
кривым Кроммелина получаем
, значит, качество обслуживания улучшилось.
Нагрузка на маркер стала меньше.
Б) Он будет работать в 2 раза медленнее:
При работе маркера в 2 раза медленнее время обслуживания одного вызова увеличится в 2 раза:
Нагрузка на маркер блока увеличится в 2 раза:
Время занятия станет:
По
кривым Кроммелина получаем
,
значит, качество обслуживания ухудшилось.
Нагрузка на маркер стала больше.
Вывод: Условные потери для каждого из направлений больше, чем явные; качество обслуживания и основные показатели работы маркера зависят от скорости работы маркера: чем быстрее работает маркер, тем лучше показатели его работы и лучше качество обслуживания.
Тема 8. Методы расчета пропускной способности однозвенных неполнодоступных включений.
Для практических расчетов пропускной способности (однозвенных неполнодоступных (НПД) включений используются приближенные методы.
Упрощенная формула Эрланга:
,
где
-
интенсивность обслуженной пучком линий
нагрузки; P-
вероятность потерь; D
-
доступность;
- средняя пропускная способность одной
линии пучка. Эта формула дает грубую
приближенную оценку пропускной
способности неполнодоступного включения
(завышается пропускная способность НПД
пучка или, что то же самое, занижается
число линий).
Формула О’Делла:
где
-
нагрузка, обслуженная полнодоступным
пучком из
линий при потерях P
и приблизительно определяемая с помощью
1-ой формулы Эрланга (по таблицам Пальма).
Формула Пальма – Якобеуса:
где А – интенсивность поступающей на пучок линий нагрузки.
При
малых значениях потерь P
можно считать
.
Поэтому все эти формулы при фиксированных
D
и P
могут быть приведены к виду:
,
где
значения
и
зависят от D
и P.
Для упрощенной формулы Эрланга:
,
Для формулы О’Делла:
;
Для формулы Пальма – Якобеуса эти коэффициенты можно подобрать. Значения и для формулы О’Делла табулированы.
8.1. Метод о’Делла.
Расчет
и построение зависимости числа линий
V и коэффициента среднего использования
от интенсивности поступающей нагрузки
А при величине потерь P=0,026, значении
доступности D=10 и 20 используя метод
О’Делла.
Значения А соответствуют нагрузкам на направлениях от АТС-4, рассчитанным при выполнении задания 3. Важное условие: V > D.
при D = 10 :
;
при D = 20 :
;
Результаты расчётов приведены в таблице 8.1.
Таблица 8.1 – Расчёты методом О’Делла.
Направление связи от АТСЭ-4 |
А, Эрл |
D=10 |
D=20 |
|||
V |
|
V |
|
|||
УСС |
13,5 |
22 |
0,61 |
20 |
0,67 |
|
ЗУC |
258,8 |
376 |
0,69 |
315 |
0,82 |
|
ЦПС |
44,8 |
67 |
0,67 |
58 |
0,77 |
|
IP-сеть |
318,4 |
461 |
0,69 |
386 |
0,82 |
|
АТСЭ – 5 |
111,8 |
164 |
0,68 |
138 |
0,81 |
|
АТСК – 2 |
56 |
84 |
0,67 |
71 |
0,79 |
|
АТСК – 3 |
39,4 |
60 |
0,66 |
51 |
0,77 |
|
АТСЭ – 4 |
129,8 |
190 |
0,68 |
160 |
0,81 |
|
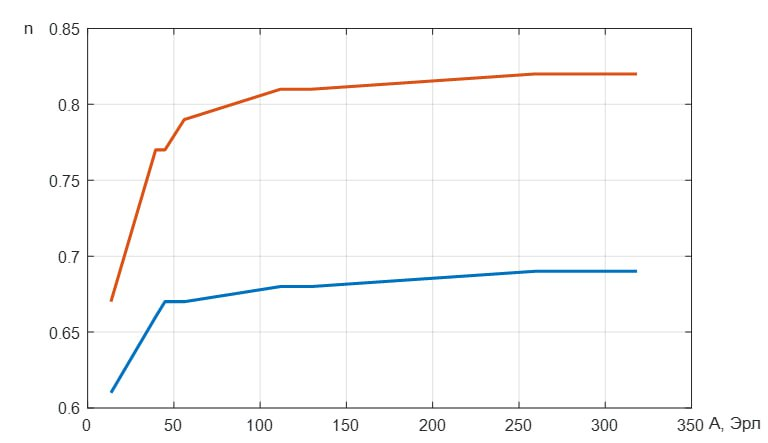
Рис. 8.1 – Зависимость коэффициента среднего использования от интенсивности поступающей нагрузки для D=10 и D=20.
Рис. 8.2 – Зависимость числа линий V от интенсивности поступающей нагрузки для D=10 и D=20.
Вывод:
По
результатам расчётов и наглядному
представлению графиков видно, что при
доступности D=10
число линий всегда больше, чем при
доступности D=20,
так же коэффициент среднего использования
при доступности D=10
находится в пределах требуемого значения
.