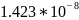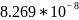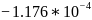- •Сортировка выбором
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев
- •Сортировка вставками
- •1) Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка пузырьком
- •1) Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка слиянием
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка шелла (последовательность хиббарда, пратта)
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев
- •Последовательность хиббарда
- •Описание алгоритма
- •Последовательность пратта
- •Описание алгоритма
- •Лучший случай:
- •2. Средний случай:
- •3. Худший случай:
- •Быстрая сортировка
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Пирамидальная сортировка
- •Описание алгоритма
- •Практическая часть
- •Сортировка выбором
- •Сортировка вставками
- •Сортировка пузырьком
- •Сортировка слиянием
- •Сортировка шелла
- •Последовательность хиббарда
- •Последовательность пратта
- •Быстрая сортировка
- •Пирамидальная сортировка
Сортировка вставками
Для экспериментальной оценки временной сложности массива сортировкой вставками было сделано 16 измерений для массивов длиной от 0 до 15000 элементов с шагом в 1000 (Таблица 2.2).
Таблица 2.3 - Экспериментальные значения для сортировки вставками
Длина массива |
Случайный |
Отсортированный |
Отсортирован по убыванию |
Отсортирован на 90% |
0 |
0.0 |
0.0 |
0.0 |
0.0 |
1000 |
0.015 |
0.0 |
0.026 |
0.0 |
2000 |
0.056 |
0.0 |
0.112 |
0.0 |
3000 |
0.129 |
0.0 |
0.260 |
0.0 |
4000 |
0.237 |
0.0 |
0.450 |
0.0 |
5000 |
0.374 |
0.0 |
0.717 |
0.0 |
6000 |
0.520 |
0.001 |
1.021 |
0.0 |
7000 |
0.705 |
0.001 |
1.398 |
0.001 |
8000 |
0.929 |
0.0 |
1.833 |
0.001 |
9000 |
1.160 |
0.0 |
2.307 |
0.001 |
10000 |
1.463 |
0.001 |
2.911 |
0.001 |
11000 |
1.734 |
0.0009 |
3.448 |
0.001 |
12000 |
2.032 |
0.001 |
4.097 |
0.001 |
13000 |
2.447 |
0.001 |
4.810 |
0.001 |
14000 |
2.805 |
0.001 |
5.573 |
0.201 |
15000 |
3.236 |
0.001 |
6.413 |
0.618 |
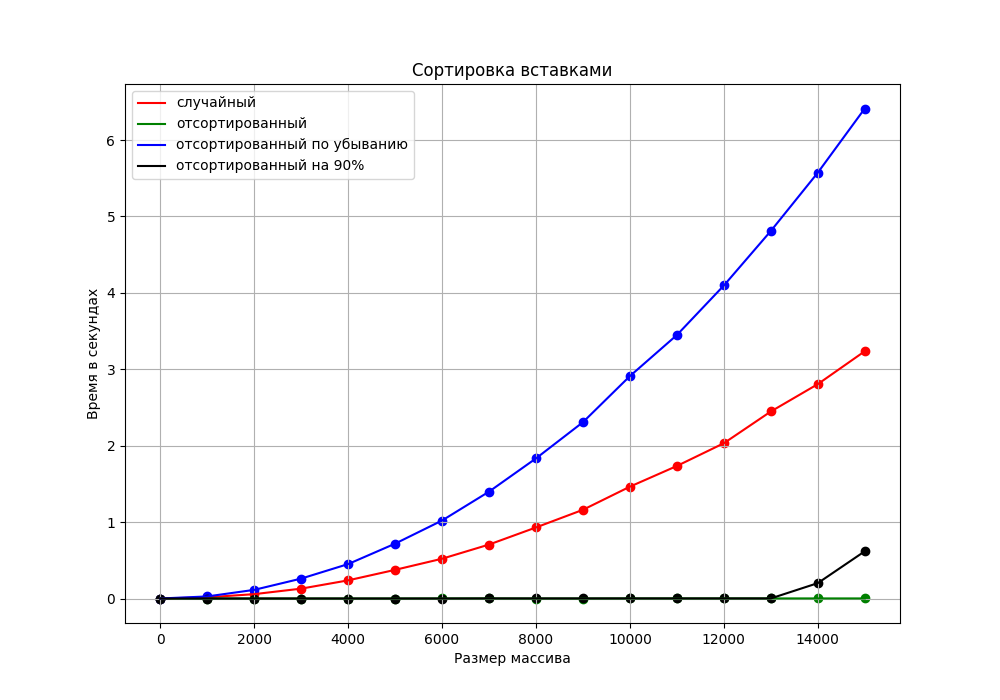
Рисунок 2.4 - График временной сложности сортировки вставками с экспериментальными значениями.

Рисунок 2.5 - График экспериментальных значений с регрессионной кривой.
Рисунок 2.6 - График временной сложности.
Таблица 2.4 - Коэффициенты моделей для сортировки вставками.
Случай |
Модель |
Коэффициенты |
||
|
|
|
||
Случайный |
|
|
|
-1.830 |
Лучший |
|
- |
|
|
Худший |
|
|
|
|
Почти отсортирован |
|
|
|
|
Сравнив график экспериментальных значений с регрессией с графиком из теоретической части, мы можем сделать вывод, что графики экспериментальных значений для всех случаев полностью совпадает с графиками временной сложности. Отсортированный массив имеет асимптотику O(n), что совпадает с теоретической частью. Также для неотсортированного массива и неполностью отсортированного массива сохраняется асимптотика O(n^2), как в теоретической части.