2. График функции временной сложности для разных случаев

Рисунок 1.3 - Временная сложность сортировки пузырьком в трех случаях.

4. Сортировка слиянием

1. Описание алгоритма

Сначала массив разбивается на две части. Этот процесс продолжается до тех пор, пока не останется массивы, состоящие из одного элемента. Массив из одного элемента уже считается отсортированным. Затем эти маленькие отсортированные массивы начинают объединяться в более крупные отсортированные массивы. При слиянии сравниваются элементы из двух массивов, и меньший элемент добавляется в новый отсортированный массив. Процесс слияния продолжается, пока не получится один отсортированный массив.

2. Устойчивость сортировки

Устойчивая: при слиянии двух отсортированных подмассивов алгоритм может сохранять порядок равных элементов, добавляя их в результирующий массив в том порядке, в котором они встречаются в исходных подмассивах.

3. Функция временной сложности и её асимптотическая оценка

Поскольку алгоритм сортировка слиянием демонстрирует одинаковую производительность вне зависимости от исходного порядка массива (лучшие, средние и худшие случаи имеют аналогичную сложность), общий подход к его анализу будет похож для всех ситуаций.

Изначально у нас есть массив длиной n. При каждом делении образуются подмассивы длиной 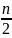. Деление продолжается до тех пор, пока не останутся массивы с длиной, равной 1, поэтому количество уровней деления можно представить как .

На каждом уровне деления происходит слияние двух подмассивов размером , которое требует n сравнений.

Обозначим функцию временной сложности так:

Рассмотрим, как происходит деление на первых трех уровнях:

Первый уровень:

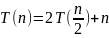
Второй уровень:

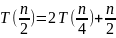
Подставим это в первое уравнение:

Третий уровень:

Подставим это в первое уравнение и получим:

Можем заметить, что 8 при T(n) и 8 в знаменателе равны третьей степени двойки. Получим общую формулу:

В случае, когда подмассив разделился на два отдельных элемента (подмассивы длиной 1), временная сложность получается

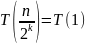
Отсюда следует

Подставим в общую формулу:

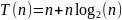
Таким образом, функция временной сложности для всех трех случаев:

Лучший случай:

Средний случай:

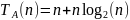
Худший случай:

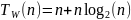
Соответственно асимптотическая оценка для всех случаев:

Лучший случай:

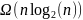
Средний случай:

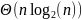
Худший случай:

4. Функция пространственной сложности и её асимптотическая оценка

Сортировка слиянием требует дополнительного пространства для временного хранения массивов, которые создаются при слиянии, поэтому пространственная сложность данного алгоритма:

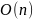
5. График функции временной сложности для разных случаев

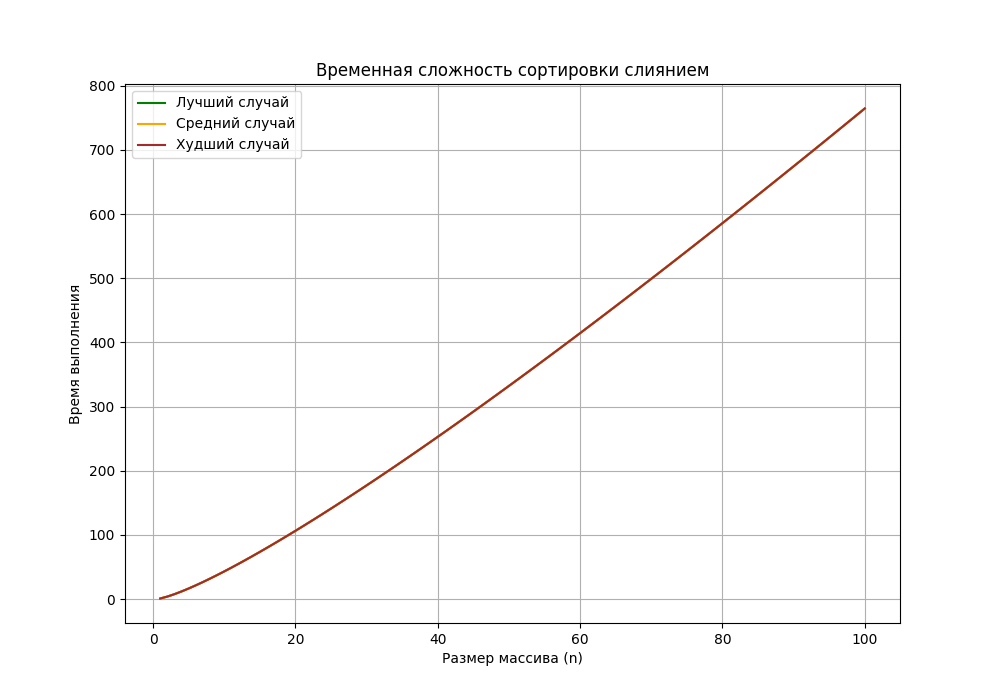
Рисунок 4.1 - Временная сложность сортировки слиянием в лучшем, среднем и худшем случаях.

5. Сортировка шелла (последовательность хиббарда, пратта)

1. Описание алгоритма

Сначала массив делится на несколько подмассивов. Это делается с помощью интервалов. Изначально интервал равен . Затем каждый из этих подмассивов сортируется с помощью обычной сортировки вставками. После сортировки подмассивов интервал уменьшается в 2 раза, и процесс повторяется. Когда шаг становится равным 1, весь массив будет отсортирован с помощью последней прохода сортировки вставками.