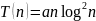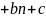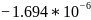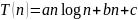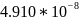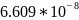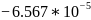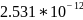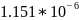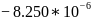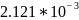- •Сортировка выбором
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев
- •Сортировка вставками
- •1) Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка пузырьком
- •1) Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка слиянием
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка шелла (последовательность хиббарда, пратта)
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев
- •Последовательность хиббарда
- •Описание алгоритма
- •Последовательность пратта
- •Описание алгоритма
- •Лучший случай:
- •2. Средний случай:
- •3. Худший случай:
- •Быстрая сортировка
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Пирамидальная сортировка
- •Описание алгоритма
- •Практическая часть
- •Сортировка выбором
- •Сортировка вставками
- •Сортировка пузырьком
- •Сортировка слиянием
- •Сортировка шелла
- •Последовательность хиббарда
- •Последовательность пратта
- •Быстрая сортировка
- •Пирамидальная сортировка
Сортировка шелла
Для экспериментальной оценки временной сложности массива сортировкой Шелла было сделано 16 измерений для массивов длиной от 0 до 15000 элементов с шагом в 1000 (Таблица 2.5).
Таблица 2.9 - Экспериментальные значения для сортировки Шелла
Длина массива |
Случайный |
Отсортированный |
Отсортирован по убыванию |
Отсортирован на 90% |
0 |
0.0 |
0.0 |
0.0 |
0.0 |
1000 |
0,001 |
0,0 |
0,001 |
0,001 |
2000 |
0,002 |
0,001 |
0,002 |
0,001 |
3000 |
0,004 |
0,002 |
0,003 |
0,002 |
4000 |
0,006 |
0,003 |
0,004 |
0,002 |
5000 |
0,008 |
0,005 |
0,007 |
0,003 |
6000 |
0,011 |
0,003 |
0,006 |
0,004 |
7000 |
0,012 |
0,004 |
0,007 |
0,005 |
8000 |
0,016 |
0,005 |
0,009 |
0,005 |
9000 |
0,018 |
0,007 |
0,011 |
0,007 |
10000 |
0,019 |
0,008 |
0,012 |
0,007 |
11000 |
0,022 |
0,007 |
0,013 |
0,007 |
12000 |
0,023 |
0,008 |
0,014 |
0,009 |
13000 |
0,027 |
0,010 |
0,016 |
0,009 |
14000 |
0,028 |
0,011 |
0,016 |
0,018 |
15000 |
0,033 |
0,011 |
0,017 |
0,023 |
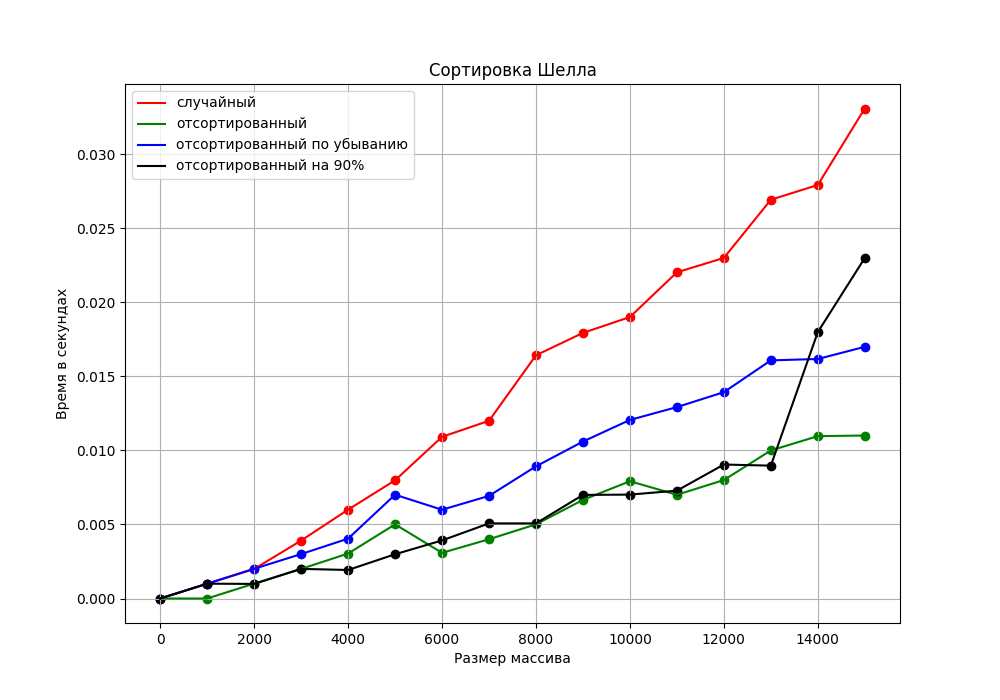
Рисунок 2.13 - График временной сложности сортировки Шелла с экспериментальными значениями.
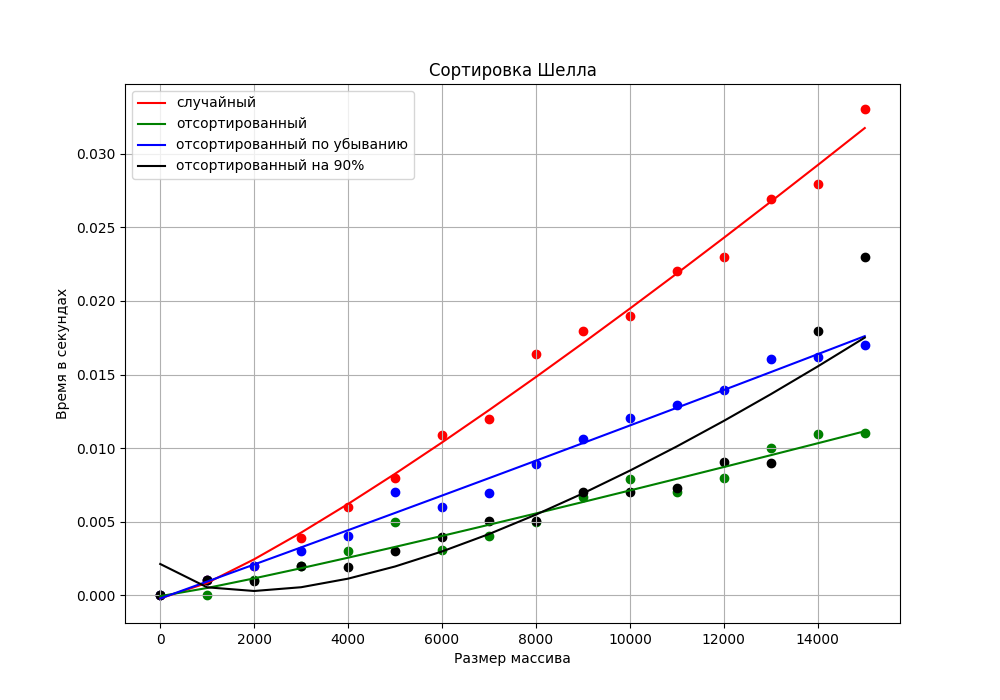
Рисунок 2.14 - График экспериментальных значений с регрессионной кривой для сортировки Шелла
Рисунок 2.15 - График временной сложности.
Таблица 2.10 - Коэффициенты моделей для сортировки Шелла.
Случай |
Модель |
Коэффициенты |
||
|
|
|
||
Случайный |
|
|
|
|
Лучший |
|
|
|
|
Худший |
|
|
|
|
Почти отсортирован |
|
|
|
|
Сравнив график экспериментальных значений с регрессией с графиком из теоретической части, мы можем сделать вывод, что графики экспериментальных значений для всех случаев сохраняют асимптотику, но для случайного массива времени на сортировку уходит больше, чем на другие случаи. Это можно объяснить тем, что в случайном массиве на больших расстояниях элементы могут находиться очень далеко друг от друга, и на начальных этапах сортировки может потребоваться много сравнений и перемещений, чтобы приблизить элементы к их правильным позициям. В то время как в отсортированном в обратную сторону массиве элементы расположены так, что на каждом шаге сортировки Шелла они могут быть перемещены к своему месту более эффективно.