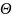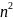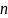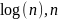- •Сортировка выбором
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев
- •Сортировка вставками
- •1) Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка пузырьком
- •1) Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка слиянием
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Сортировка шелла (последовательность хиббарда, пратта)
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев
- •Последовательность хиббарда
- •Описание алгоритма
- •Последовательность пратта
- •Описание алгоритма
- •Лучший случай:
- •2. Средний случай:
- •3. Худший случай:
- •Быстрая сортировка
- •Описание алгоритма
- •Устойчивость сортировки
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для разных случаев
- •Пирамидальная сортировка
- •Описание алгоритма
- •Практическая часть
- •Сортировка выбором
- •Сортировка вставками
- •Сортировка пузырьком
- •Сортировка слиянием
- •Сортировка шелла
- •Последовательность хиббарда
- •Последовательность пратта
- •Быстрая сортировка
- •Пирамидальная сортировка
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра САПР
отчет
по лабораторной работе №1
по дисциплине «Алгоритмы и структуры данных»
Тема: Алгоритмы сортировки сравнением
Студентка гр. 3352 |
|
|
Преподаватель |
|
|
Санкт-Петербург
2024
Цель работы: реализация алгоритмов сортировки сравнением и исследование их временной сложности.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Задачи:
Даны следующие алгоритмы сортировки сравнением: сортировка выбором, сортировка вставками, сортировка пузырьком, сортировка слиянием, сортировка Шелла (последовательность Шелла, Хиббарда, Пратта) быстрая сортировка, пирамидальная сортировка. Теоретическая часть: Для каждого алгоритма сортировки.
Написать асимптотическую временную и пространственную сложность (таблица).
Описать алгоритм сортировки (своими словами).
Проанализировать устойчивость алгоритма сортировки.
Получить функцию временной сложности для лучшего, среднего и худшего случая.
Получить асимптотическую оценку временной сложности для лучшего, среднего и худшего случая.
Получить функцию пространственной сложности и её асимптотическую оценку.
Построить график функции временной сложности для лучшего, худшего и среднего случая. Вывести графики функции временной сложности в среднем случае на одно изображение и сделать предположение о наибыстрейшей сортировке в среднем случае при размере массива > 100 000.
Таблица 1 - Асимптотическая временная и пространственная сложность сортировок
Сортировка |
Асимптотическая
временная сложность,
|
Пространственная сложность, |
||
Лучший случай |
Средний случай |
Худший случай |
||
Выбором |
|
|
|
|
Вставками |
|
|
|
|
Пузырьком |
|
|
|
|
Слиянием |
|
|
|
|
Шелла |
|
|
|
|
Быстрая |
|
|
|
|
Пирамидальная |
|
|
|
|
Сортировка выбором
Описание алгоритма
Массив делится на две части: отсортированную и неотсортированную. Сначала мы находим в неотсортированной части минимальное значение и меняем его с первым элементом этой же части. Тем самым отсортированный массив увеличился на единицу. Следующий поиск минимального числа будет происходить в неотсортированной части массива, длина которого, наоборот, уменьшилась на единицу. Таким образом, увеличиваясь с каждым прогоном на единицу, отсортированная часть массива становится равной по длине изначальному массиву.
Устойчивость сортировки
Неустойчивая: при нахождении минимального элемента и его замене с текущим элементом, порядок равных элементов может измениться, если они находятся в разных частях массива.
Функция временной сложности и её асимптотическая оценка
Лучший случай.
Функция
состоит из внешнего цикла (от 0 до
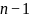 )
и внутреннего цикла, где элемент имеет
индекс
)
и внутреннего цикла, где элемент имеет
индекс
 (от
до
(от
до
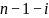 ).
).
Процесс сравнения будет происходить даже при отсортированном массиве, так как на каждой итерации нужно найти минимальный элемент. Значит количество сравнений будет равно сумме:

В отсортированном массиве будет происходит обмен найденного минимального элемента с самим собой. Значит количество обменов будет равно сумме:
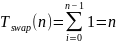
Таким образом, функция сложности:

Асимптотическая
оценка:

Средний случай
Количество сравнений остается таким же, как и при отсортированном массиве:

Будем считать, что в среднем случае будет происходить половина всех возможных обменов.

Таким образом, функция сложности:
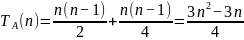
Асимптотическая
оценка:
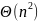
Худший случай
В этом случае количество сравнений остается прежним, так как массив отсортирован в обратном порядке:
При этом количество обменов будет тоже равняться:
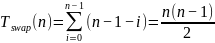
Таким образом, функция сложности:
 )
)
Асимптотическая
оценка:
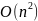
Функция пространственной сложности и её асимптотическая оценка
Алгоритм
сортировки выбором не требует
дополнительной памяти для хранения
элементов, кроме переменных для индексов
и временного хранения при обмене.
Поэтому, пространственная сложность
данного алгоритма:

График функции временной сложности для всех случаев

Рисунок 1.1 - Временная сложность сортировки выбором в трех случаях.
Сортировка вставками
1) Описание алгоритма
Массив делится на две части: отсортированную и неотсортированную. Мы запоминаем второй элемент неотсортированной части массива и осуществляем с ним следующую операцию: пока наш элемент строго меньше чем предыдущий, сдвигаем все элементы вправо на один. После чего наш элемент вставляется в конец отсортированной части, увеличивая её на один. Таким, образом, увеличиваясь с каждым прогоном на единицу, отсортированная часть массива становится равной по длине изначальному массиву.
Устойчивость сортировки
Устойчивая: алгоритм вставляет элементы в отсортированную часть массива, перемещая элементы только тогда, когда это необходимо. Таким образом, равные элементы сохраняют свой первоначальный порядок.