Расчётная часть

В таблице 1 представлены результаты измерений скорости счета образцов и первичной обработки.

1. Радиометрировали каждый препарат из 2 комплектов. Первый комплект состоял из 8 препаратов (1 серия), второй из 6 препаратов (2 серия).

№ п/п | I, имп/мин	1 серия	2 серия
1	965	988
2	1085	1093
3	925	977
4	1027	1152
5	1123	1012
6	1016	870
7	1034	-
8	1089	-
	1033,00	1015,33
S2	4364,86	9611,87

Таблица 1. Результаты измерений скорости счета и первичной обработки результатов

2. Расчёт выборочного среднего ( ) и ( ) и выборочной дисперсии ( и )

Для серии 1: ( ))= (∑I₁ )/n = (965+1085+…+1089)/8 =1033

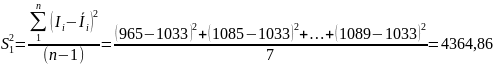
Для серии 2 расчеты аналогичны, как и для серии 1:

( ))= (∑I₂ )/n = (988+1093+…+870)/6 =1015,33

3. Проверка гипотезы об однородности дисперсий

Расчет эмпирического значения критерия Фишера:

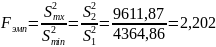
Сравниваем эмпирический и критический значения критерия Фишера при заданном уровне значимости

2,202<5,28, следовательно, F_эмп <F_крит

F_эмп не превышает критическое значение для уровня значимости 0,05 при числах степеней свободы f₁=7 и f₂ =5, следовательно гипотеза об однородности дисперсий принимается, т. е. выборочные дисперсии и можно считать независимыми оценками общей генеральной дисперсии σ².

Поэтому можем рассчитать сводную дисперсию по обеим выборкам:

4. Проверка гипотезы об однородности математических ожиданий

Расчет эмпирического значения критерия Стьюдента

Сравниваем эмпирический и критический значения критерия Стьюдента при заданном уровне значимости

0,831<2,179, следовательно, t_эмп <t_крит

T_эмп не превышает критическое значение для уровня значимости 0,05 при числе степеней свободы f=12, следовательно, гипотеза об однородности математических ожиданий принимается, различие между выборочными средними признается статистически незначимым.

Значит две выборки взяты из одной генеральной совокупности, и оценками генеральных параметров может быть сводная дисперсия и средневзвешенное, рассчитанное по формуле:

5. Проверка гипотезы об подчинении выборки распределению Пуассона

Число степеней свободы для нашей выборки: f= n₁ + n₂ − 2 = 8 + 6 – 2 = 12

Вычислим критерий Пирсона:

Сравниваем эмпирическое и критическое значения при заданном уровне значимости.

76,66 > 21,026 следовательно

Критерий Пирсона превышает критическое значение для уровня значимости 0,05 при числе степеней свободы f=12, следовательно, гипотеза об отсутствии статистически значимого расхождения между эмпирическим и теоретическим отвергается. Поэтому выдвигаем гипотезу «об отсутствии грубых погрешностей»:

Где

2,461> 1,689, следовательно, ζ_p=0,05> ζ_mx

2,261> 2,074, следовательно, ζ_p=0,05> ζ_min

Проверка гипотезы о наличии грубых погрешностей закончилась тем, что эта гипотеза отвергается.

6. Оценка результатов измерения радиоактивности. Доверительный интервал для определяемого параметра.

Т.к. пуассоновская гипотеза была отвергнута на определенном уровне значимости и в списке результатов нет грубых погрешностей, интервальную оценку истинной скорости счета рассчитываем с использованием распределения Стьюдента:

Получаем

Выводы

Полученные в ходе лабораторной работы результаты измерения активности относятся к одной генеральной совокупности (подтвердились гипотезы об однородности дисперсий и математических ожиданий).

Для нахождения доверительного интервала результатов измерений выборка была исследована на подчинение распределению Пуассона. Но данная гипотеза была отвергнута на данном уровне значимости и в результатах не были найдены грубые погрешности, поэтому интервальную оценку рассчитывали с помощью распределения Стьюдента.