Министерство науки и высшего образования Российской Федерации ФГАОУ ВО «Уральский федеральный университет имени первого
Президента России Б.Н. Ельцина»
Физико-технологический институт
Кафедра радиохимии и прикладной экологии
Лабораторная работа № 3.1 и 3.2
Проверка гипотезы о подчинении результатов измерения активности распределению Пуассона.
Преподаватель |
|
Недобух Т.А. |
Студенты |
|
Хитрых А.В. Сапунов А.Г. |
Группа |
|
Фт – 320016 |
|
|
|
Екатеринбург
2025г.
Цель работы: Проверить гипотезу о подчинении результатов измерения активности распределению Пуассона
Задачи:
Измерить с фоном один произвольно выбранный препарат по одной минуте несколько раз;
Сформировать первую серию измерений;
Этот же препарат измерить столько же раз, произвольно поворачивая вокруг своей оси;
Сформировать вторую серию измерений;
Все полученные закрытые радиоактивные препараты радиометриуют;
Для каждой серии измерений рассчитать выборочное среднее и выборочную дисперсию;
Исследовать пуассоновский характер разброса результатов для каждой серии;
В зависимости от исхода, принять или отвергнуть нулевую гипотезу, при необходимости выдвинуть и проверяют гипотезу о грубых погрешностях;
Сделать выводы о подчинении результатов измерения активности распределению Пуассона и о вкладе различных видов погрешности в разброс результатов измерения активности.
Теоретическая часть
В случае радиометрических измерений наряду с другими погрешностями в результат вносится дополнительная неопределенность, обусловленная вероятностным характером самого радиоактивного распада.
1. Распределение Пуассона описывает вероятность появления определенного числа событий за фиксированный интервал времени или пространства, если эти события происходят с известной средней интенсивностью и независимо друг от друга.
Формула распределения Пуассона:
Пуассоновский поток событий характеризуется стационарностью, отсутствием последействия и ординарностью.
Стационарность: вероятность попадания событий в интервал времени зависит только от длины этого интервала.
Отсутствие последействия: число событий в одном интервале не зависит от числа событий в другом неперекрывающемся интервале.
Ординарность: вероятность попадания более одного события в элементарный интервал пренебрежимо мала.
2. Для проверки гипотезы используется критерий согласия Пирсона χ2.
Если χ2 превышает критическое значение для заданного уровня значимости, гипотеза отвергается.
3. Для выявления грубых погрешностей используется критерий наибольшего нормированного отклонения.
Расчётная часть
В таблице 1 представлены результаты измерений скорости счета образцов и первичной обработки.
Таблица 1. Результаты измерений скорости счета и первичной обработки результатов
-
№ п/п
1 Серия
2 Серия
3 Серия
I, имп/мин
1
90
92
126
2
106
124
615
3
101
148
672
4
122
131
658
5
105
111
567
6
108
126
624
7
117
121
601
8
108
106
568
9
118
-
644
10
-
-
607
11
-
-
590
Icp
108,33
119,88
570,18
S2
95,25
288,41
22844,36
Среднее значение скорости счёта и дисперсии, для каждой серии, рассчитывалось как:
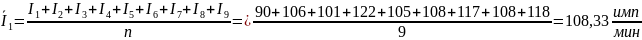
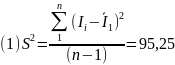
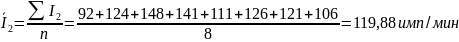
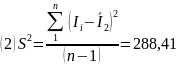
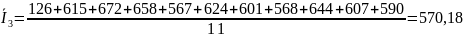
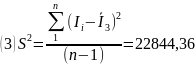
Генеральная дисперсия величины I, рассчитывалась как:
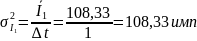
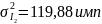
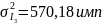
Расчет эмпирического значения критерия Пирсона:
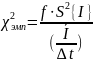
Для первой серии: f = n – 1 = 9 – 1 = 8
;
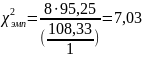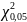= 15,51;
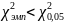
Эмпирические значение не превышает критическое для уровня значимости 0,05 при числе свободы f = 8, следовательно, гипотеза об отсутствии статистически значимого расхождения между эмпирическим и теоретическим принимается.
Погрешности, обусловленные статистической природой радиоактивного распада и случайными погрешностями, связанными, например, с нестабильностью работы аппаратуры являются не значимыми.
Для второй серии: f = 8 – 1 = 7
;
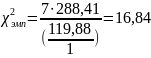= 14,01;
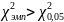
Эмпирические значение превышает критическое для уровня значимости 0,05 при числе свободы f = 7, следовательно, гипотеза об отсутствии статистически значимого расхождения между эмпирическим и теоретическим не принимается.
Для третьей серии: f = 11– 1 = 10
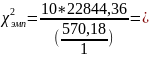400,65;
= 18,307;
Эмпирические значение превышает критическое для уровня значимости 0,05 при числе свободы f = 10, следовательно, гипотеза об отсутствии статистически значимого расхождения между эмпирическим и теоретическим не принимается.
Гипотеза о подчинении разброса данных распределению Пуассона для серий 2 и 3 была отвергнута на основании критерия Пирсона, поэтому выдвигаем гипотезу «об отсутствии грубых погрешностей».
Для серии 2:
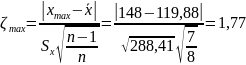
Где
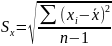
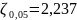
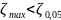
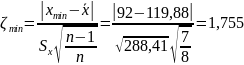
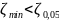
Проверка гипотезы о наличии грубых погрешностей для второй серии опыта закончилась тем, что эта гипотеза отвергается.
Для третьей серии:
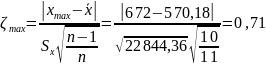
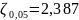
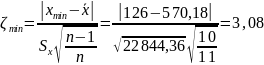
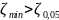
Проверка гипотезы о наличии грубой погрешности закончилась тем, что эта гипотеза принимается, т.е. некоторый «подозрительно выпадающий» результат, как отягощенный грубой погрешностью, можно будет отбросить (исключить из списка).
Теперь снова вернёмся к проверке гипотезы о пуассоновском характере распределения результатов радиометрии, располагая списком данных, меньшим на одно значение.
Для третьей серии исключим 1 номер так как он является «подозрительно выпадающим» результатом. И проведем расчет заново:
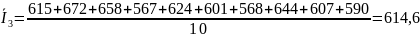
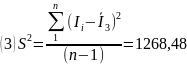
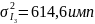
Расчет эмпирического значения критерия Пирсона:
f = 10 - 1 = 9
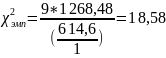
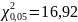
Эмпирические значение превышает критическое для уровня значимости 0,05 при числе свободы f = 9, следовательно, гипотеза об отсутствии статистически значимого расхождения между эмпирическим и теоретическим не принимается. Выдвигаем гипотезу «об отсутствии грубых погрешностей».
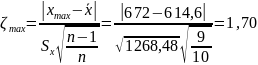
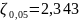
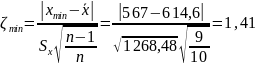
Проверка гипотезы о наличии грубых погрешностей для второй серии опыта закончилась тем, что эта гипотеза отвергается.
Выводы
Полученные в ходе лабораторной работы результаты измерения активности подчиняются распределению Пуассона. Для результатов 2 серии подчинение распределению стало возможным лишь после исключения из результатов значений, отягощенных грубой погрешностью. Для 3 серии опыта пришлось исключить некоторый «подозрительно выпадающий» результат, как отягощенный грубой погрешностью и подчинение распределению стало возможным лишь после исключения из результатов значений, отягощенных грубой погрешностью.
Измерение любой физической величины с абсолютной точностью невозможно, следовательно, в результате измерения мы получаем значение, отягощенное погрешностью. Различают систематические, случайные погрешности и грубые промахи. Появление систематических погрешностей вызывается факторами, действующими одинаковым образом при выполнении измерений одним и тем же методом, одним и тем же измерительным устройством, что приводит к «параллельному сдвигу» относительно истинного значения или изменению в соответствии с каким-то законом.
Наибольший вклад в разброс результатов измерений вносят отклонения – грубые погрешности (промахи), которые необходимо исключать после соблюдения определенных статистических процедур. Однако и в тех случаях, когда систематическая погрешность настолько мала, что можно ею пренебречь, а грубые погрешности не наблюдаются, результаты измерений не свободны от погрешностей. Рассеяние результатов может быть обусловлено неконтролируемым изменением большого числа неподдающихся учету факторов, оказывающих влияние на процесс измерения. Погрешности такого типа называются случайными.
Лабораторная работа № 3.2