
Лекция 4
.pdfМетоды и средства диагностирования
Лекция 4
3.3Методы статистических решений
3.3.1Метод минимального риска
3.3.2Метод минимального числа ошибочных решений
3.3.3Метод наибольшего правдоподобия
3.3.4Метод минимакса
3.3.5Метод Неймана-Пирсона
Методы статистических решений
•Рассматриваемые в этой лекции методы также относятся к статистическим. Однако они отличаются от методов, изложенных в прошлой лекции, правилами принятия решения.
•Здесь решающее правило выбирается исходя из некоторых условий оптимальности, например из условия минимума риска.
•Возникшие в математической статистике как методы проверки статистических гипотез (работы Неймана и Пирсона), рассматриваемые методы нашли широкое применение в радиолокации (обнаружение сигналов на фоне помех), радиотехнике, общей теории связи и других областях.
2
•Рассмотрим сначала процесс распознавания при наличии одного диагностического параметра.
•х — диагностический параметр
•D1 — исправное состояние
•D2 — наличие дефекта
3
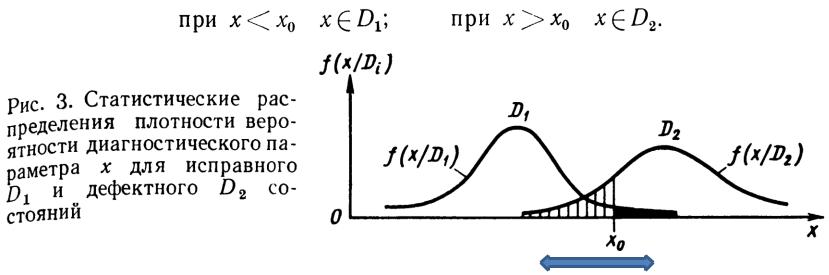
Правило решения
•Пусть производится диагностика состояния газотурбинного двигателя по содержанию железа в масле (параметр х). Задача
состоит в выборе значения х0 параметра х таким образом, что при х > х0 следует принимать решение о снятии двигателя с эксплуатации, а при х < х0 допускать дальнейшую работу.
•Так как состояние системы характеризуется одним параметром, то система имеет одномерное пространство признаков.
•Разделение производится на два класса (дифференциальная
диагностика или дихотомия). Условимся считать: D1 — исправное состояние и D2 — наличие дефекта.
•Тогда указанное правило решения состоит в следующем:
4

Ложная тревога и пропуск цели (дефекта)
•Ложной тревогой называется случай, когда принимается решение о наличии дефекта, но в действительности система находится в исправном состоянии (вместо D1 принимается D2).
•Пропуск цели (дефекта) — принятие решения об справном
состоянии, тогда как система содержит дефект (вместо D2 принимается D1).
5

Очевидно, что эти двоякого рода ошибки могут иметь различные последствия или различные цены.
Обозначим Hi,j (i, j = 1, 2) возможные решения по правилу
(1)
(первый нижний индекс соответствует индексу принятого диагноза, второй — индексу действительного состояния).
Тогда Н12 — пропуск дефекта и Н21 — ложная тревога (D1 — исправное состояние, D2 — дефектное состояние); Н11 и Н22 — правильные решения.
6

Вероятность ложной тревоги равна вероятности произведения двух событий: наличие исправного состояния и значения х > х0:
где Р1 = Р (D1) —априорная вероятность диагноза D1 (считается известной на основании предварительных статистических данных).
Подобным образом находится вероятность пропуска дефекта:
7

Средний риск
•Вероятность принятия ошибочного решения слагается из вероятностей ложной тревоги и пропуска дефекта. Если приписать «цены» этим ошибкам, то получим выражение для среднего риска
•Разумеется, цена ошибки имеет условное значение, но она должна учесть предполагаемые последствия ложной тревоги и пропуска дефекта. В задачах надежности стоимость пропуска дефекта обычно существенно
больше стоимости ложной тревоги (C12 >> С21). Иногда вводится цена правильных решений Н11 и Н22, которая для сравнения со стоимостью потерь (ошибок) принимается отрицательной.
•В общем случае средний риск (ожидаемая величина потери) выражается равенством
(2)
8
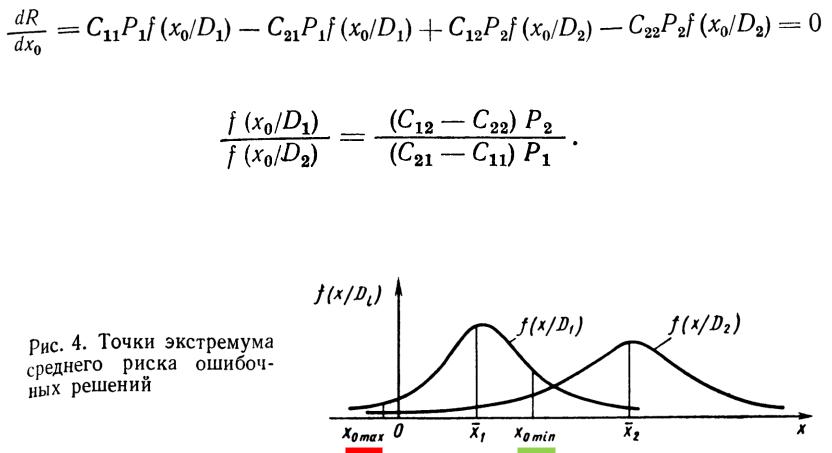
1. Метод минимального риска
Найдем граничное значение х0 из условия минимума среднего риска. Дифференцируя (2) по х0 и приравнивая производную нулю, получим сначала условие экстремума
или
(3)
Это условие часто определяет два значения x0, из которых одно соответствует минимуму, второе — максимуму риска
9

•Соотношение (3) является необходимым, но недостаточным условием минимума.
•Для существования минимума R в точке х = х0 вторая производная должна быть положительной т.е. d2R/dx02 > 0, что приводит к следующему условию относительно производных плотностей распределений:
(4)
•Если распределения f(x/D1) и f(x/D2) содержат не более одной точки максимума, то при
условие (4) выполняется.
10
