И осуществляется переход к шагу 6. Т.К. Указанное условие в данном случае не соблюдается ( , то переходим к шагу 5.

Шаг 5. Вычисляются нормированные параметры распределения с помощью выражения 

значения коэффициентов полинома   приводятся в таблице 2.1.

Таблица 1

j	0	1	2
a0	0.78760454	-0.23350401*101	0.19935077
a1	-0.25889486	0.88266373	-0.10402411
a2	-0.31872153	0.99215448*10-1	-0.7659968*10-2
a3	0.45243271*10-1	-0.52450713*10-1	0.64909123*10-2
a4	-0.27552103*10-2	0.62824786*10-2	-0.83410484*10-3
a5	0	-0.240757*10-3	0.33025782*10-4

Шаг 6. Определяются ненормированные значения параметров распределения

Шаг 7. Вычисляются значения параметров распределения, соответствующие исходному интервалу [17; 18,7]:

Отсюда получим: f(x)=  .

Задание 2.2

Проверка гипотезы о нормальном распределении выборки с помощью критерия   .

X_min=17, x_max=18,7

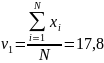
Разобьем интервал [17;18,7] на 5 частей: [17;17,34), [17,34;17,68), [17,68;18,02), [18,02;18,36), [18,36;18,7]

Номер интервала	mi	pi	Npi
1	6	0,12	3,6	1,6
2	6	0,22	6,6	0,05
3	8	0,26	7,8	0,005
4	3	0,19	5,7	1,28
5	7	0,09	2,7	6,8

По заданному уровню значимости   найдем   . Сопоставив   с   =13,28, можем заключить, что гипотеза о нормальном распределении не противоречит фактическим данным.

Проверка гипотезы о нормальном распределении выборки с помощью критерия Колмогорова.

Оценка плотности распределения:  ,тогда   .

Xi	F(x)	Fнорм(x)	F(x)-Fнорм(x)
17,0	0,16	0,05	0,11
17,1	0,2	0,08	0,12
17,1	0,2	0,08	0,12
17,2	0,25	0,11	0,14
17,2	0,25	0,11	0,14
17,3	0,3	0,15	0,15
17,4	0,36	0,21	0,15
17,5	0,42	0,27	0,15
17,5	0,42	0,27	0,15
17,6	0,49	0,34	0,15
17,6	0,49	0,34	0,15
17,6	0,49	0,34	0,15
17,7	0,55	0,42	0,13
17,7	0,55	0,42	0,13
17,7	0,55	0,42	0,13
17,7	0,55	0,42	0,13
17,8	0,62	0,5	0,12
17,9	0,68	0,57	0,11
17,9	0,68	0,57	0,11
18,0	0,74	0,65	0,09
18,1	0,79	0,72	0,07
18,2	0,84	0,78	0,06
18,3	0,89	0,84	0,05
18,4	0,92	0,88	0,04
18,5	0,95	0,91	0,04
18,5	0,95	0,91	0,04
18,5	0,95	0,91	0,04
18,6	0,98	0,94	0,04
18,6	0,98	0,94	0,04
18,7	0,99	0,96	0,03
		МАКС	0,15