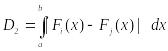ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

УФИМСКИЙ УНИВЕРСИТЕТ НАУКИ И ТЕХНОЛОГИИ

Кафедра технической кибернетики

ПОСТРОЕНИЕ КЛАССИФИКАЦИОННЫХ ШКАЛ С УЧЕТОМ СТАТИСТИЧЕСКИХ ОСОБЕННОСТЕЙ ДАННЫХ

Вариант -17

Выполнил: студент гр. ИВТ-227б

Мустафина К. И.

Проверил: профессор каф. ТК

Гвоздев В. Е.

Уфа 2023

Цель работы: Изучение специальных статистических методов анализа малых выборок.

Задание на работу:

Задание №1:

1.1. На основе выборочных данных (таблица 2 приложения) построить оценки законов распределения наработки до отказа следующими методами:

• последовательных медиан;

• уменьшения неопределенности;

• сжатия ИЗР.

1.2. Составить полученные оценки на основе следующих метрик:

• 

• 

• 

Где i, j – идентификаторы используемых методов (i, j =   );

a, b – границы области изменения случайной величины x

Задание №2:

1. На основе выборочных данных (Таблица 2 приложения), построить оценку неусеченного закона распределения.

2. Произвести сопоставление полученной оценки с нормальным законом распределения, у которого математическое ожидание и среднеквадратическое отклонение определены по выборочным данным Сопоставление произвести на основе метрик ХИ-квадрат и F-критерия Колмогорова (см. работу «Построение оценок законов распределения случайных величин по выборочным данным»).

Ход работы:

Исходные данные:

X	17
1	18,5
2	17,2
3	17,1
4	18,6
5	18,0
6	17,4
7	18,2
8	17,9
9	17,7
10	18,1
11	17,2
12	17,6
13	18,6
14	17,5
15	17,7
16	17,7
17	17,1
18	18,7
19	18,4
20	17,9
21	17,5
22	17,6
23	18,3
24	17,3
25	18,5
26	17,7
27	18,5
28	17,8
29	17,0
30	17,6

Задание №1.1:

Метод последовательных медиан

Изначально исходные данные {x₁, x₂,..., x_N} располагаются в вариационный ряд, находится медиана этого ряда и на графике эмпирической функции распределения ставится точка с координатами   и   =0.5. Затем находятся медианы двух половин вариационного ряда и им в соответствие ставятся значения эмпирической функции 0.25 и 0.75 и т.д. Указанная процедура продолжается до тех пор, пока не будут рассмотрены все имеющиеся значения x_i(i=1,2,...,N). В результате получается ряд точек F_n (х).

Нахождение начального и конечного значений функций распределения осуществляется по формулам:

где 

Медиана выборки: 

Таблица последовательных медиан и значений эмпирической функции распределения:

16,9	0
17	0,0625
17,1	0,125
17,2	0,1875
17,35	0,25
17,5	0,3125
17,6	0,375
17,7	0,4375
17,85	0,5
18	0,5625
18,1	0,625
18,2	0,6875
18,35	0,75
18,5	0,7625
18,6	0,875
18,7	0,9375
18,8	1

По полученным данным был построен график функции распределения, изображенный на рисунке 1.

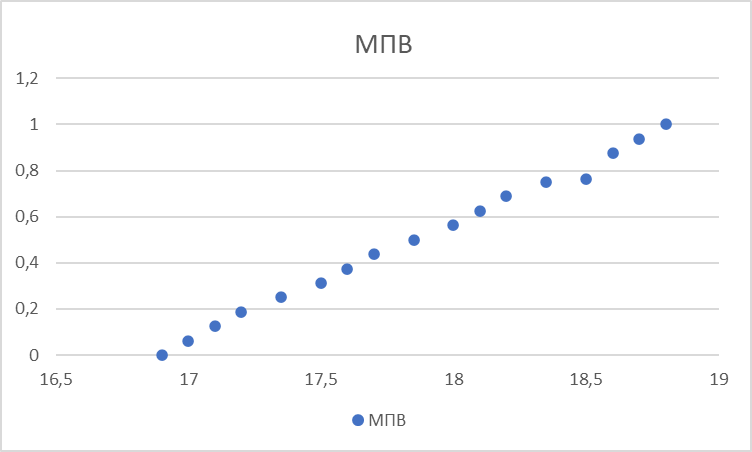
Рисунок 1. График функции распределения

Метод уменьшения неопределенности

Выражение для эмпирической функции распределения, получаемой с помощью МУН, записывается в виде: 

при x_i-1xx_i и 

где   - число одинаковых значений x_i. МУН является частный.

При расчете получились следующие значения F(x_i):

17,0	0,00
17,1	0,07
17,1	0,10
17,2	0,13
17,2	0,17
17,3	0,17
17,4	0,20
17,5	0,27
17,5	0,30
17,6	0,37
17,6	0,40
17,6	0,43
17,7	0,50
17,7	0,53
17,7	0,56
17,7	0,59
17,8	0,60
17,9	0,60
17,9	0,63
18,0	0,63
18,1	0,67
18,2	0,70
18,3	0,74
18,4	0,77
18,5	0,87
18,5	0,90
18,5	0,93
18,6	0,93
18,6	0,97
18,7	0,97

График функции распределения, полученный методом уменьшения неопределенности представлен на рисунке 2.

Рисунок 2. График функции распределения

Метод сжатия ИЗР

Наиболее предпочтительным при инженерных расчетах является алгоритм, основанный на минимизации дисперсии. В этом случае члены ряда (7) определяются следующим образом: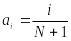 

Рассчитанные значения a_i:

xi	i	ai
17,0	1	0,03
17,1	2	0,06
17,1	3	0,10
17,2	4	0,13
17,2	5	0,16
17,3	6	0,19
17,4	7	0,23
17,5	8	0,26
17,5	9	0,29
17,6	10	0,32
17,6	11	0,35
17,6	12	0,39
17,7	13	0,42
17,7	14	0,45
17,7	15	0,48
17,7	16	0,52
17,8	17	0,55
17,9	18	0,58
17,9	19	0,61
18,0	20	0,65
18,1	21	0,68
18,2	22	0,71
18,3	23	0,74
18,4	24	0,77
18,5	25	0,81
18,5	26	0,84
18,5	27	0,87
18,6	28	0,90
18,6	29	0,94
18,7	30	0,97

Полученный график изображен на рисунке 3.

Рисунок 3. График функции распределения

Задание 1.2

Составить полученные оценки на основе следующих метрик:

• 

• 

• 

F(xi)	F(x)	ai
0	0,00	0,03
0,0625	0,07	0,06
0,125	0,10	0,10
0,1875	0,13	0,13
0,25	0,17	0,16
0,25	0,17	0,19
0,3125	0,20	0,23
0,375	0,27	0,26
0,4375	0,30	0,29
0,5	0,37	0,32
0,5	0,40	0,35
0,5625	0,43	0,39
0,625	0,50	0,42
0,6875	0,53	0,45
0,75	0,56	0,48
0,75	0,59	0,52
0,7625	0,60	0,55
0,875	0,60	0,58
0,9375	0,63	0,61
1	0,63	0,65
	0,67	0,68
	0,70	0,71
	0,74	0,74
	0,77	0,77
	0,87	0,81
	0,90	0,84
	0,93	0,87
	0,93	0,90
	0,97	0,94
	0,97	0,97

D1:

	1	2	3
1	0	0,16	0,08
2	0,16	0	0,08
3	0,08	0,08	0

D2:

	1	2	3
1	0	0,19	0,18
2	0,19	0	0,04
3	0,18	0,04	0

D3:

	1	2	3
1	0	0,04	0,03
2	0,04	0	0,002
3	0,03	0,002	0

Ответы на контрольные вопросы первой части:

1. В чем заключается основная идея метода прямоугольных вкладов?

Методика построения f(x), основывается на использовании в качестве функции вклада единичного прямоугольника, что и дало название методу. Плотность распределения при этом записывается в виде:

 , (2)

 - функция вклада единичной площади. При этом для некоторых значений x_i функция вклада может выходить за пределы интервала [a,b]. В этом случае часть площади, выходящая за границы интервала, отбрасывается, а над оставшимся основанием прямоугольника равномерно надстраивается площадь, равная отброшенной.

2. Условия применимости метода прямоугольных вкладов;

Во-первых, для определения формы вклада используются значения четвертого центрального момента; во-вторых, для определения оптимальных значений параметров требуется априорное значение типа распределения. Если тип распределения заранее неизвестен, обосновать выбор значений параметров не представляется возможным.

3. В чем отличие метода уменьшения неопределенности от метода прямоугольных вкладов? 

Отличие МУН от МПВ заключается в том, что вместо прямоугольного вклада ширины d, построенного около реализации x_i, используется нормированное равномерное распределение, заданное на интервале [x_i-1,x_i+1] суть МУН заключается в равномерном распределении скачка вероятности в точке x_i.

4. Почему в качестве априорной компоненты метода прямоугольных вкладов целесообразно использовать равномерное распределение?

МПВ основывается на использовании априорной информации о неизвестном распределении и учете случайного характера выбора. Априорная информация о распределении состоит в следующем:

• при известных границах [a,b] интервала, на котором определена случайная величины X, плотность распределения удовлетворяет условию:

f(x)0 x[a,b]

f(x)=0 x[a,b]

• плотность распределение непрерывна внутри интервала [a,b] и не имеет очень крутых подъемов и спадов.

Из анализа априорной информации можно заключить, что в качестве априорной компоненты в МПВ наиболее целесообразно использовать равномерное распределение, заданное внутри интервала [a,b].

Учет случайного характера выборки выражается в том, что учитывается возможность появления любых других значений случайной величины из области [x_i  d/2; x_i + d/2], где d - ширина вклада.

5. Преимущества и недостатки метода сжатия области существования интегральных законов распределения.

Основным достоинством метода сжатия ИЗР является возможность вычислить доверительную вероятность для каждого i-го члена последовательности: 0  a₁  a₂  ...  a_i  ...  a_N  1

При этом вероятность прохождения ИЗР через заранее выбранный интервал [a_i_I, a_i+_I] определяется как   , где   - плотность вероятности прохождения ИЗР на уровне y_i для i-го испытания в серии из N испытаний. Эта величина описывается выражением 

Кроме того, использование метода сжатия ИЗР обеспечивает высокую точность оценивания функции распределение в окрестности узлов интерполяции.

Недостатком метода является то, что точность воспроизведения остальных участков кривой у= F(x) путем линейной интерполяции при малом числе наблюдений невысока.