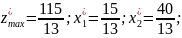В) Симплекс-алгоритм.
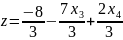
Выразим базисные переменные через свободные:
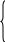
При увеличении функция увеличивается быстрее, поэтому:
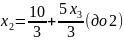
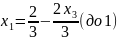
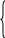
Выразим , с учетом этого пересчитаем :
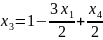
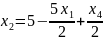
Найдем базисное решение:
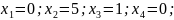
Решение является допустимым базисным.
Проверим его на оптимальность:
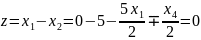
Данное решение не является оптимальным.
При
увеличении
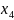функция увеличивается быстрее, поэтому:
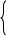
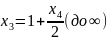
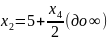
Полученный результат означает, что допустимые решения есть, но оптимального решения нет, поскольку целевая функция неограниченно убывает.
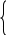
Задача 3:
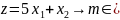
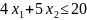(1)
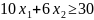(2)
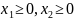
а) Геометрический метод.
ОДР задана неравенствами, это стандартная задача и ее можно решить геометрическим методом.
Построим область допустимых решений, удовлетворяющих указанным выше условиям.
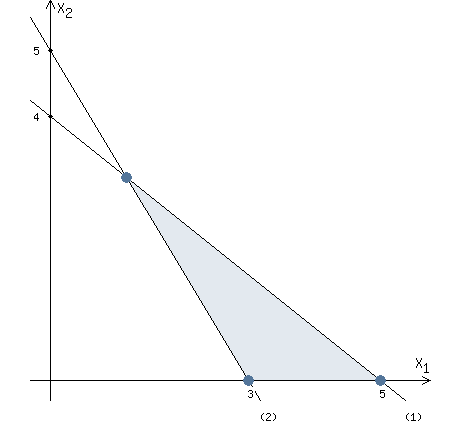
Построим линию уровня и перемещаем ее перпендикулярно вектору
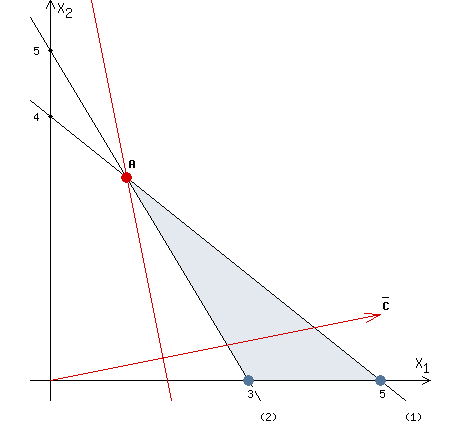
Функция F достигает наименьшего значения в точке A.
Найдем координаты точки A.
Точка A одновременно принадлежит прямым (1) и (2)
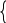
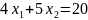
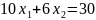
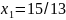
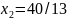
Минимальное значение функции z = 115/13
Ответ:
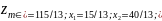
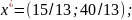
б) Допустимое базисное решение.
Приведем задачу к каноническому виду
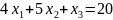
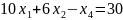
j=
Так как в каждом уравнении есть переменные, которых нет в других, то система уравнений линейно-независимая. Ранг системы r=2. То есть базисных переменных 2. Пусть – базисные, а – свободные. Выразим базисные переменные через свободные:
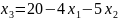
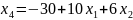
Базисное решение:
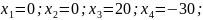
Данное решение не является допустимым. Решим систему методом искусственных переменных. Переменная отрицательная. Недопустимой является только одна базисная переменная, выражение которой получается из второго уравнения. Поэтому введем искусственную переменную только в это уравнение.
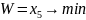
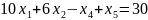
j=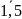
Пусть – базисные, а – свободные. Выразим базисные переменные через свободные
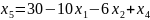
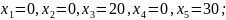
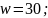
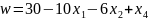
При увеличении функция увеличивается быстрее, поэтому:
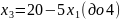
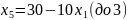
Выразим , с учетом этого пересчитаем :
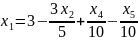
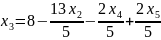
Найдем базисное решение:
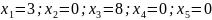
Решение является допустимым базисным.
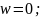
Так как w = 0, найденное решение является допустимым базисным для исходной системы.
В) Симплекс-алгоритм.
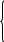
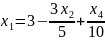
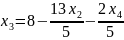
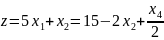
При увеличении функция увеличивается быстрее, поэтому:
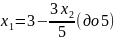
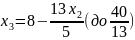
Выразим , с учетом этого пересчитаем :
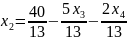
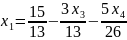
Найдем базисное решение:
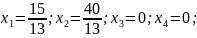
Решение является допустимым базисным.
Проверим его на оптимальность:
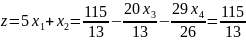
Данное решение является оптимальным.
Следовательно,
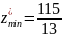
Ответ:
