
ФГБОУ ВО
Уфимский государственный авиационный технический университет
Кафедра технической кибернетики
100 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
90 |
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к расчётно-графической работе
по дисциплине «Методы оптимизации»
Тема: «Решение задач линейного программирования (ЛП)»
Вариант №10

1304.417003.000 ПЗ
(обозначение документа)
ИВТ-217 Группа |
Фамилия, И., О. |
Подпись |
Дата |
Оценка |
Студент |
Саляхов А.Ф. |
|
|
|
Консультант |
Хасанов А.Ю. |
|
|
|
Принял |
Хасанов А.Ю. |
|
|
|
Уфа 2023 г.
Задача 1:

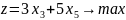
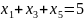
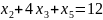
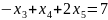
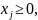 j=
j=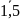
А) Геометрический метод.
Область допустимых решений (ОДР) задана равенствами, задача не является стандартной.
Сократим количество переменных:
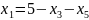

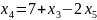
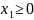 ,
,
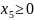

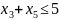 (1)
(1)
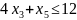 (2)
(2)
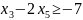 (3)
(3)
Теперь ОДР задана неравенствами, получилась стандартная задача и ее можно решить геометрическим методом.
Построим область допустимых решений, удовлетворяющих указанным выше условиям.
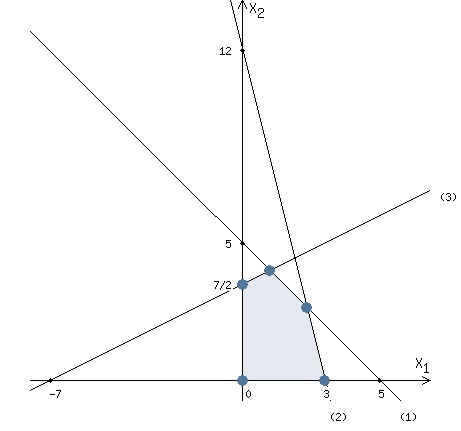
Построим
линию уровня и перемещаем ее перпендикулярно
вектору

Функция F достигает наибольшего значения в точке A.
Найдем координаты точки A.
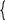
Точка A одновременно принадлежит прямым (1) и (3).
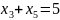
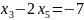
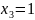
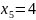
Найдем базисные переменные:
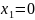
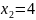
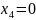
Максимальное значение функции z = 23
Ответ:
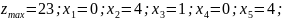
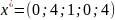
б) Допустимое базисное решение.
Система представлена в каноническом виде:
j=
Так
как в каждом уравнении есть переменные,
которых нет в других, то система уравнений
линейно-независимая. Ранг системы r=3.
То есть базисных переменных 3. Пусть
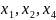 – базисные, а
– базисные, а
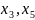 – свободные. Выразим базисные переменные
через свободные:
– свободные. Выразим базисные переменные
через свободные:

Базисное решение:
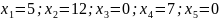
Данное решение является допустимым
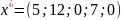
в) Симплекс-алгоритм.
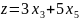
Решение не оптимально - в ЦФ есть положительные коэффициенты.
Выразим базисные переменные через свободные:
При
увеличении
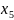 функция увеличивается быстрее, поэтому:
функция увеличивается быстрее, поэтому:
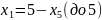
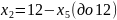
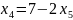 (до
3,5)
(до
3,5)

Выразим
,
с учетом этого пересчитаем
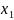 и
и
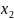 :
:
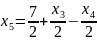
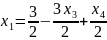
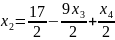
Найдем базисное решение:
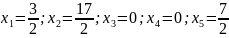
Решение является допустимым базисным.
Проверим его на оптимальность:
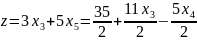
Данное решение не является оптимальным.
При
увеличении
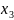 функция увеличивается быстрее, поэтому:
функция увеличивается быстрее, поэтому:
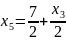
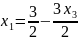
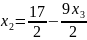
Выразим , с учетом этого пересчитаем и :
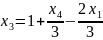
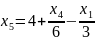
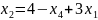
Найдем базисное решение:
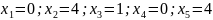
Решение является допустимым базисным.
Проверим его на оптимальность:
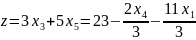
Данное решение является оптимальным.
Следовательно,
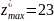
Ответ:

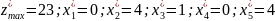
Задача 2:
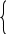
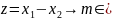
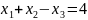
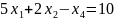
j=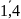
А) Геометрический метод.
Область допустимых решений (ОДР) задана равенствами, задача не является стандартной.
Сократим количество переменных:

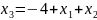
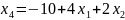
,
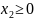

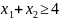 (1)
(1)
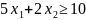 (2)
(2)
Теперь ОДР задана неравенствами, получилась стандартная задача и ее можно решить геометрическим методом.
Построим область допустимых решений, удовлетворяющих указанным выше условиям.
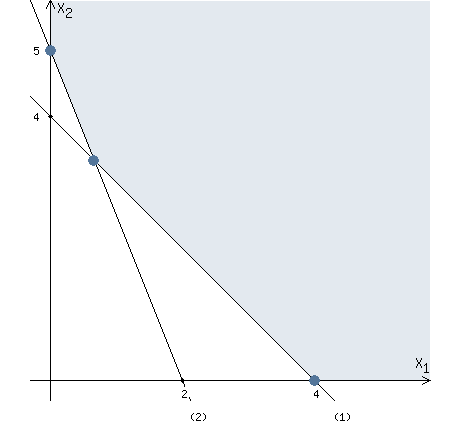
Из рисунка видно, что задача не имеет решение т.к функция z неограниченно убывает.
Б) Допустимое базисное решение.
Система представлена в каноническом виде:

j=
Так
как в каждом уравнении есть переменные,
которых нет в других, то система уравнений
линейно-независимая. Ранг системы r=2.
То есть базисных переменных 2. Пусть
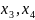 – базисные, а
– базисные, а
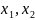 – свободные. Выразим базисные переменные
через свободные:
– свободные. Выразим базисные переменные
через свободные:

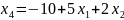
Базисное решение:
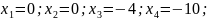
Данное решение не является допустимым. Решим систему методом искусственных переменных.
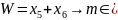

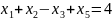
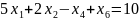
j=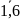
Пусть
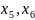 – базисные, а
– базисные, а
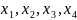 – свободные. Выразим базисные переменные
через свободные
– свободные. Выразим базисные переменные
через свободные
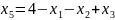
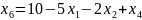
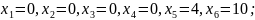
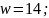
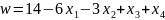
При увеличении функция увеличивается быстрее, поэтому:

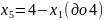
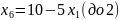

Выразим , с учетом этого пересчитаем :
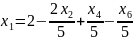
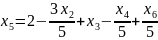
Найдем базисное решение:
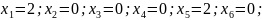
Решение является допустимым базисным.
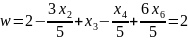
При увеличении функция увеличивается быстрее, поэтому:

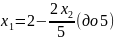
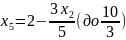
Выразим , с учетом этого пересчитаем :
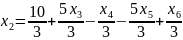
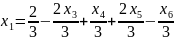
Найдем базисное решение:
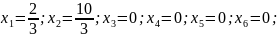
Решение является допустимым базисным.
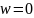
Так как w = 0, найденное решение является допустимым базисным для исходной системы.
