Лабораторная работа №2

ФБГОУ ВО

Уфимский государственный авиационный технический университет

Кафедра ТК

ОТЧЕТ

по лабораторной работе №2

по дисциплине «Методы оптимизации»

Тема: «Методы одномерной оптимизации, использующие производные»

Вариант № 10

Выполнил: ст. гр. ИВТ-217

Саляхов А.Ф.

Проверил: доцент каф. ТК

Хасанов А.Ю.

Уфа 2023

Целевая функция:

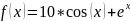
Область неопределенности: [1.3; 3]

График функции:

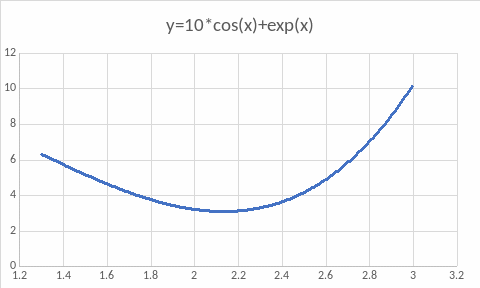
Проверка применимости методов, использующих производные, к заданной целевой функции на заданном отрезке локализации. Критерием применимости является выпуклость целевой функции на заданном отрезке локализации.

График функции f (x):

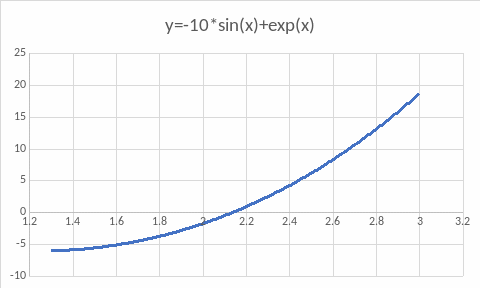
График функции f (x):

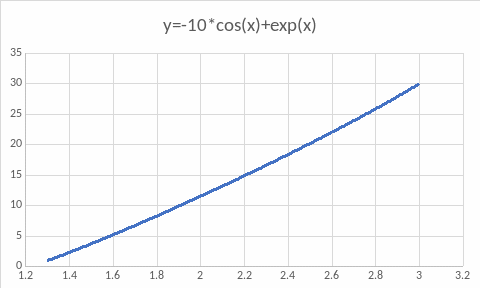
Расчетные таблицы:

Метод Фибоначчи
N	x	y	E1	Eg	E0	K
10	2.1309	3.1097	0.0495722	0.00955056	0.00959831	9
20	2.13455	3.10961	0.000640628	7.80422e-005	7.80422e-005	19
30	2.1345	3.10961	3.99044e-007	6.31343e-007	6.34531e-007	29
40	2.1345	3.10961	2.55913e-007	7.5064e-009	5.15913e-009	39
50	2.1345	3.10961	4.20107e-006	-2.93423e-007	4.19469e-011	49

Метод средних
N	x	y	E1	Eg	E0	K
10	2.13423	3.10961	0.00374539	0.000830078	0.000830078	10
20	2.1345	3.10961	4.22325e-007	8.10623e-007	8.10623e-007	20
30	2.1345	3.10961	3.60484e-009	7.19624e-010	7.91624e-010	30
40	2.1345	3.10961	1.06297e-013	7.73159e-013	7.7307e-013	40
50	2.1345	3.10961	1.77636e-015	6.66134e-016	7.54952e-016	50

Метод касательных
N	x	y	K	E1	Eg
10	2.25222	3.20982	10	1.74198	0.208057
20	2.13296	3.10963	20	0.021255	0.00656316
30	2.1344	3.10961	30	0.00142672	0.00020539
40	2.13451	3.10961	40	7.85837e-005	6.41842e-006
50	2.1345	3.10961	50	1.66056e-006	2.00302e-007

Метод хорд
N	x	y	K	E1	Eg
10	2.1340644311221029	3.1096153131733102	10	0.0060081190131118234	0.86593556887789713
20	2.1345000275786927	3.1096140044505347	20	2.2343842509542355e-007	0.86549997242130727
30	2.1345000437739468	3.1096140044505329	30	8.3026918673567707e-012	0.86549995622605325
40	2.1345000437745485	3.1096140044505312	40	1.7763568394002505e-015	0.86549995622545151
50	2.1345000437745485	3.1096140044505312	50	1.7763568394002505e-015	0.86549995622545151

Метод Ньютона
N	x	y	k	E1
10	2.1345	3.10961	10	1.97314e-006
20	2.1345	3.10961	20	1.77636e-015
30	2.1345	3.10961	30	1.77636e-015
40	2.1345	3.10961	40	1.77636e-015
50	2.1345	3.10961	50	1.77636e-015

Код программы

#include <stdafx.h>

#include <iostream>

#include <stdlib.h>

#include <locale.h>

#include <complex>

#include <math.h>

#include <string.h>

#include <fstream>

#include <conio.h>

#include <iomanip>

#include <Windows.h>

using namespace std;

const int G = 10000;

double f(double x)

{

return (10*cos(x)+exp(x));

}

double dfdx(double x)

{

return (10*(-sin(x))+exp(x));

}

double dfdx2(double x)

{

return (-10*cos(x)+exp(x));

}

long long fibo(int n)

{

long long* fibonum = new long long[n + 1];

fibonum[0] = 1; fibonum[1] = 1;

for (int m = 2; m <= n; m++)

fibonum[m] = fibonum[m - 1] + fibonum[m - 2];

return fibonum[n];

}

void fibonacci()

{

SetConsoleCP(1251);

SetConsoleOutputCP(1251);

int i, j, N;

double a, b, xe, ye, min, E1, x1, x2, y1, y2, Eras, k = 0, d, Egar;

cout << "Вы выбрали метод чисел Фибоначчи." << endl;

cout << "Введите длину отрезка а и b; число экспериментов N" << endl;

cout << "a = "; cin >> a;

cout << "b = "; cin >> b;

cout << "N = "; cin >> N;

cout << endl;

x1 = a + (b - a) * fibo(N - 2) / fibo(N);

y1 = f(x1);

x2 = a + (b - a) * fibo(N - 1) / fibo(N);

y2 = f(x2);

k = 2;

d = (b - a) / (2 * fibo(N)) / 100;

Eras = (b - a) / (2 * fibo(N)) + d / 2;

while (k < (N - 1))

{

if (y1 < y2)

{

b = x2; x2 = x1; y2 = y1;

x1 = a + b - x2; y1 = f(x1);

}

else

{

a = x1; x1 = x2; y1 = y2;

x2 = a + b - x1; y2 = f(x2);

}

k = k + 1;

}

if (y1 < y2)

{

b = x2; x2 = x1; y2 = y1;

}

else

a = x1;

x1 = x2 - d; y1 = f(x1);

if (y1 < y2)

b = x2;

else

a = x1;

xe = (a + b) / 2; ye = f(xe);

cout << "a = " << a << endl;

cout << "b = " << b << endl;

Egar = (b - a) / 2; E1 = abs(dfdx(xe));

cout << "Полученные значения: " << endl;

cout << "x = " << xe << endl;

cout << "y = " << ye << endl;

cout << "Гарантированная точность = " << Egar << endl;

cout << "Точность = " << E1 << endl;

cout << "Расчетная точность = " << Eras << endl;

cout << "Фактическое число экспериментов = " << k << endl;

_getch();

}

void srednih()

{

SetConsoleCP(1251);

SetConsoleOutputCP(1251);

int i, k;

double d, x, y, Egar = 0, a, b, Eras, N, z, E1, xe, ye;

bool flag = true;

cout << "Вы выбрали метод средних." << endl;

cout << "Введите длину отрезка а и b; число экспериментов N " << endl;

cout << "a = "; cin >> a;

cout << "b = "; cin >> b;

cout << "N = "; cin >> N;

k = 0;

Eras = (b - a) / (pow(2.0, N)) / 2;

while (k < N)

{

x = (a + b) / 2; z = dfdx(x); k += 1;

if (z == 0)

{

E1 = 0; Egar = 0;

xe = x; ye = f(xe); flag = false;

break;

}

else

{

if (z > 0)

b = x;

else

a = x;

}

}

if (flag == true)

{

Egar = (b - a) / 2;

xe = (a + b) / 2;

ye = f(xe); E1 = abs(dfdx(xe));

}

cout << "Полученные значения: " << endl;

cout << "x = " << xe << endl;

cout << "y = " << ye << endl;

cout << "Гарантированная точность = " << Egar << endl;

cout << "Точность = " << E1 << endl;

cout << "Расчетная точность = " << Eras << endl;

cout << "Фактическое число экспериментов = " << k << endl;

system("pause");

return;

}

void kasat()

{

SetConsoleCP(1251);

SetConsoleOutputCP(1251);

int i, k;

double d, x, y, Egar = 0, a, b, N, z, E1, xe, ye, z1, z2, x1, x2, y1, y2;

bool flag = true;

cout << "Вы выбрали метод касательных." << endl;

cout << "Введите длину отрезка а и b; число экспериментов N " << endl;

cout << "a = "; cin >> a;

cout << "b = "; cin >> b;

cout << "N = "; cin >> N;

y1 = f(a); y2 = f(b);

z1 = dfdx(a); z2 = dfdx(b);

k = 4;

while (k < N)

{

x = ((z2 * b - z1 * a) - (y2 - y1)) / (z2 - z1); y = f(x); z = dfdx(x); k += 2;

if (z == 0)

{

E1 = 0; Egar = 0;

xe = x; ye = y;

flag = false;

break;

}

else

{

if (z > 0)

{

b = x; y2 = y; z2 = z;

}

else

{

a = x; y1 = y; z1 = z;

}

}

}

if (flag == true)

{

Egar = b - a;

xe = x;

ye = y; E1 = abs(z);

}

cout << "Полученные значения: " << endl;

cout << "x = " << xe << endl;

cout << "y = " << ye << endl;

cout << "Гарантированная точность = " << Egar << endl;

cout << "Точность = " << E1 << endl;

cout << "Фактическое число экспериментов = " << k << endl;

_getch();

}

void hord()

{

SetConsoleCP(1251);

SetConsoleOutputCP(1251);

int i, k;

double d, x, y, Egar = 0, a, b, N, z, E1, xe, ye, z1, z2;

bool flag = true;

cout << "Вы выбрали метод хорд." << endl;

cout << "Введите длину отрезка а и b; число экспериментов N " << endl;

cout << "a = "; cin >> a;

cout << "b = "; cin >> b;

cout << "N = "; cin >> N;

z1 = dfdx(a); z2 = dfdx(b);

k = 2;

while (k < N)

{

x = a - (z1 / (z2 - z1)) * (b - a); z = dfdx(x); k += 1;

if (z == 0)

{

E1 = 0; Egar = 0;

xe = x; ye = f(xe);

flag = false;

break;

}

else

{

if (z > 0)

{

b = x; z2 = z;

}

else

{

a = x; z1 = z;

}

}

}

if (flag == true)

{

Egar = b - a;

xe = x;

ye = f(xe); E1 = abs(dfdx(xe));

}

cout << "Полученные значения: " << endl;

cout << setprecision(20) << "x = " << xe << endl;

cout << "y = " << ye << endl;

cout << "Гарантированная точность = " << Egar << endl;

cout << "Точность = " << E1 << endl;

cout << "Фактическое число экспериментов = " << k << endl;

_getch();

}

void newton()

{

SetConsoleCP(1251);

SetConsoleOutputCP(1251);

int i, k;

double d, x, y, a, b, N, z, E1, xe, ye, u;

bool flag = true;

cout << "Вы выбрали метод Ньютона." << endl;

cout << "Введите длину отрезка а и b; число экспериментов N " << endl;

cout << "a = "; cin >> a;

cout << "b = "; cin >> b;

cout << "N = "; cin >> N;

x = b;

z = dfdx(x); u = dfdx2(x);

k = 2;

while (k < N)

{

if (z == 0)

break;

else

{

x = x - z / u;

z = dfdx(x);

u = dfdx2(x);

k += 2;

}

}

E1 = abs(z); xe = x; ye = f(xe);

cout << "Полученные значения: " << endl;

cout << "x = " << xe << endl;

cout << "y = " << ye << endl;

cout << "Точность = " << E1 << endl;

cout << "Фактическое число экспериментов = " << k << endl;

_getch();

}

int main()

{

SetConsoleCP(1251);

SetConsoleOutputCP(1251);

int j;

while (1)

{

system("cls");

cout << "1 Метод чисел Фибоначчи \n";

cout << "2 Метод средних\n";

cout << "3 Метод касательных\n";

cout << "4 Метод хорд\n";

cout << "5 Метод Ньютона\n";

cout << "6 Выход из программы\n";

cout << "Ваш выбор (1-6):";

cin >> j;

switch (j)

{

case 1: fibonacci(); break;

case 2: srednih(); break;

case 3: kasat(); break;

case 4: hord(); break;

case 5: newton(); break;

case 6: cout << "Завершение программы\n";

system("pause");

return(1);

default: cout << j << "Нет такого пункта в меню\n";

system("pause");

}

}

}

Блок-схемы функций методов

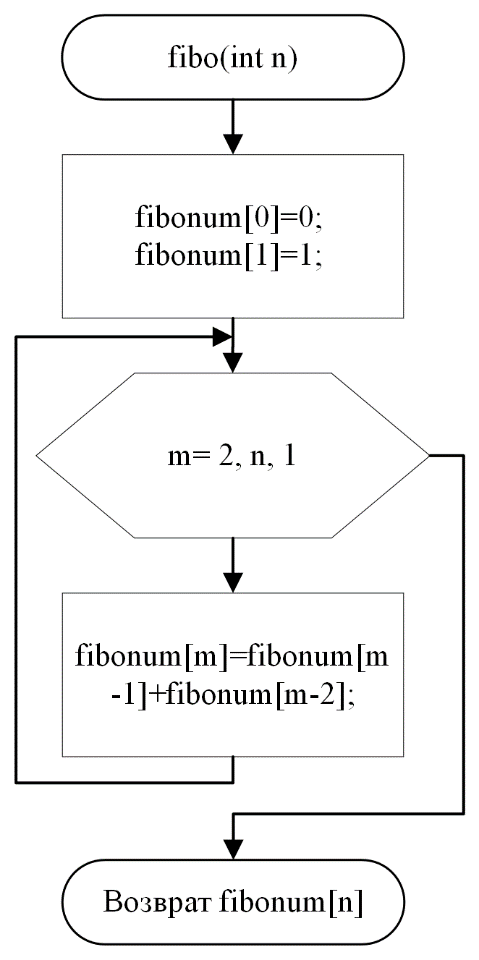
Блок-схема функции вычисления чисел Фибоначчи

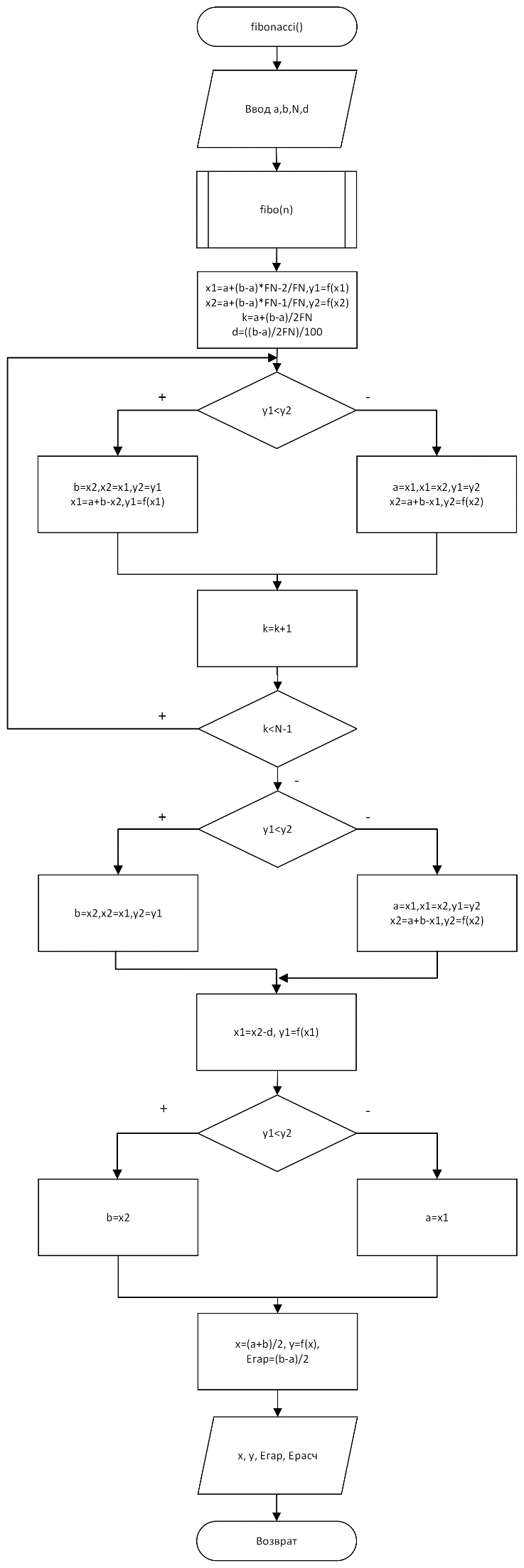
Блок-схема метода чисел Фибоначчи

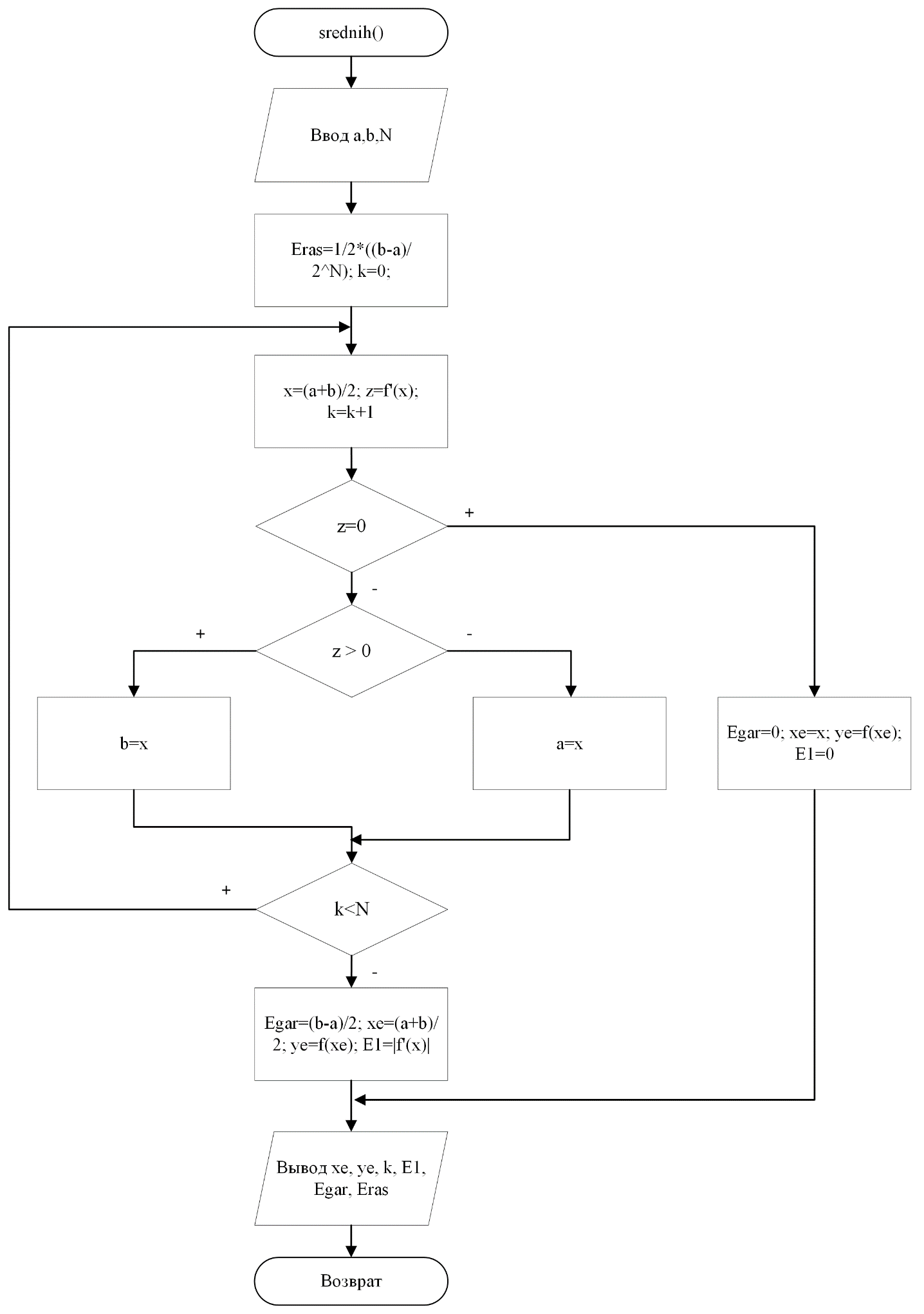
Блок-схема функции метода средних

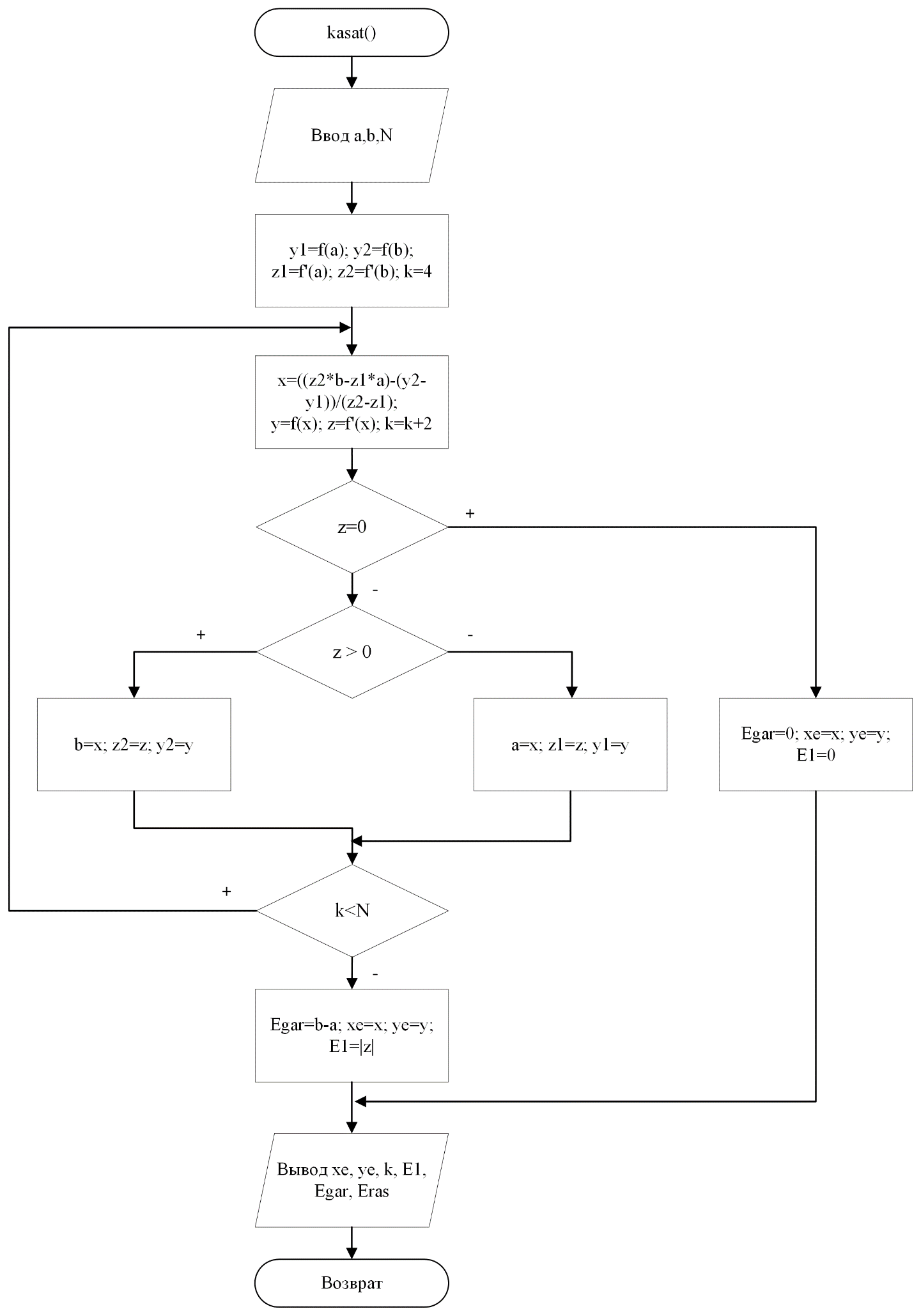
Блок-схема функции метода касательных

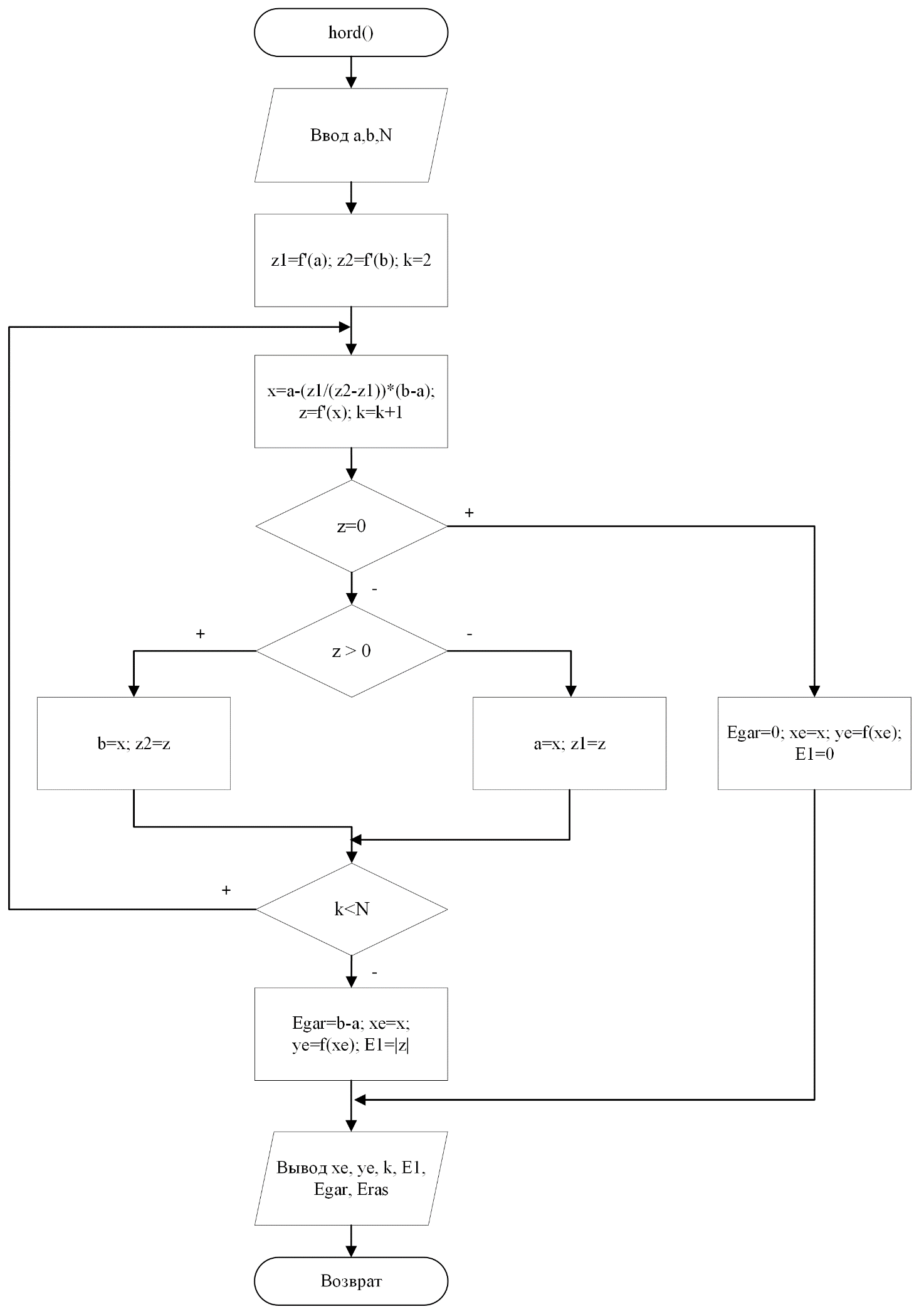
Блок-схема функции метода хорд

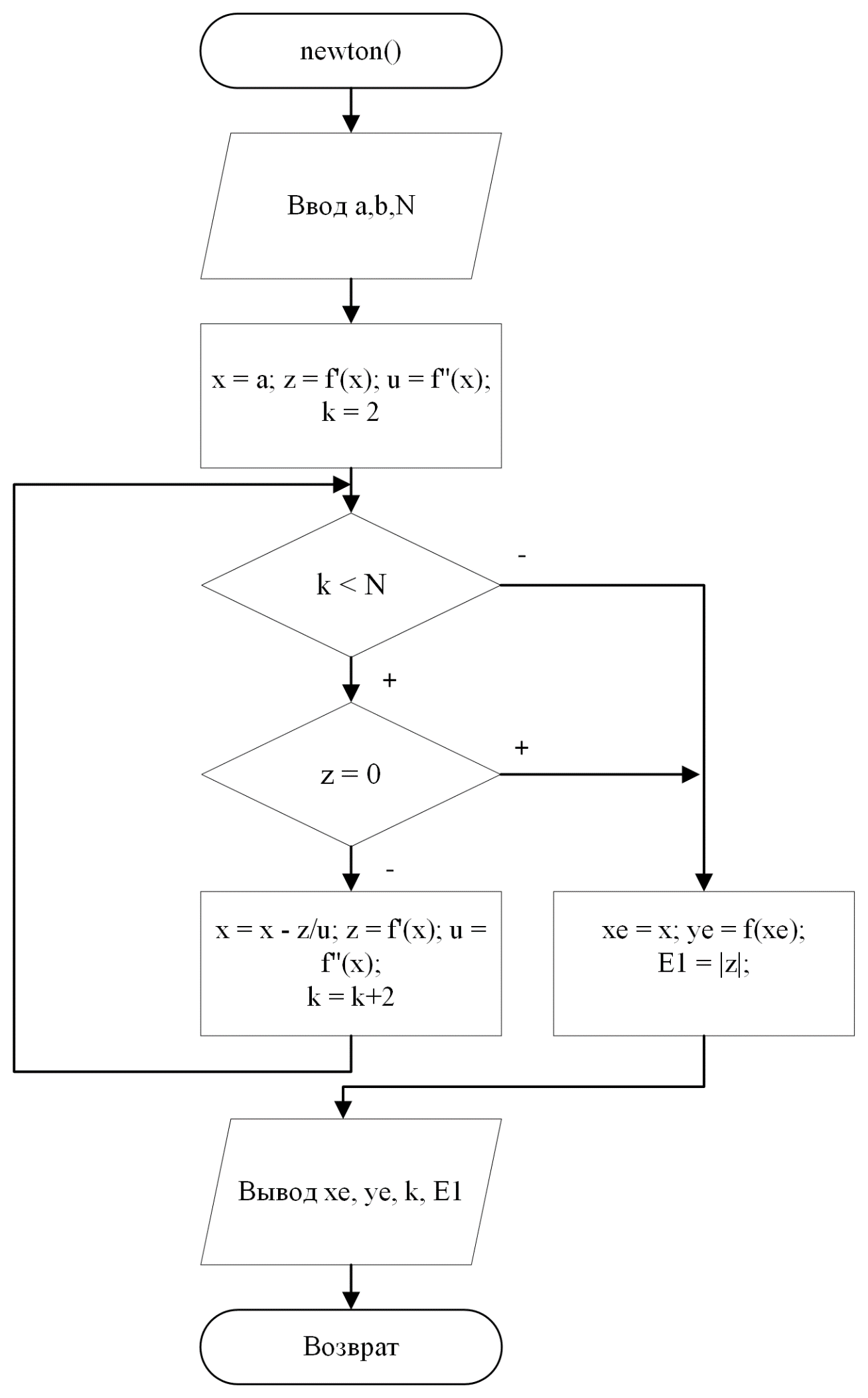
Блок-схема метода Ньютона