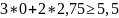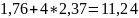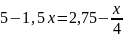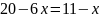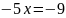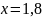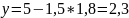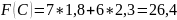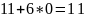ФГБОУ ВО «Уфимский университет науки и технологий»

Лабораторная работа №2

«Анализ чувствительности оптимального решения»

Вариант 20

Выполнил: ст. гр. ИВТ-429Б

Саляхов А.Ф.

Проверил: старший преподаватель кафедры АСУ

Кондратьева О.В.

Уфа 2025

Цель работы: провести анализ чувствительности оптимального решения, проанализировав все ресурсы.

Ход работы:

При откорме каждое животное должно получать не менее Б ед. белков, У ед. углеводов и П ед. протеина. Для составления рациона используют два вида корма, представленных в следующей таблице:

Питательные вещества	Количество единиц питательных веществ на 1кг		Минимальное кол-во
	Корма 1 вида	Корма 2 вида
Белки	3	2		10
Углеводы	1	4		11
Протеин	1	6		16

Стоимость 1 кг корма первого вида – 7 д.е., второго – 6 д.е. Составьте дневной рацион питательности, имеющий минимальную стоимость

Математическая модель:

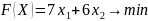
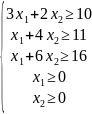
ОДЗ:

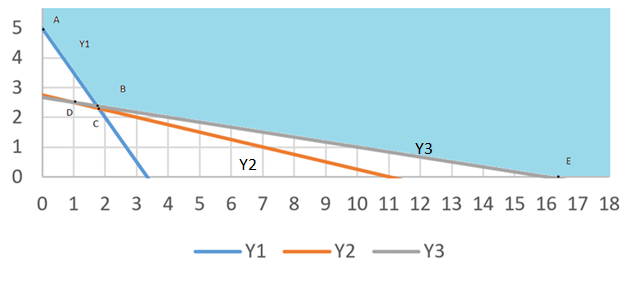
Точка оптимума:

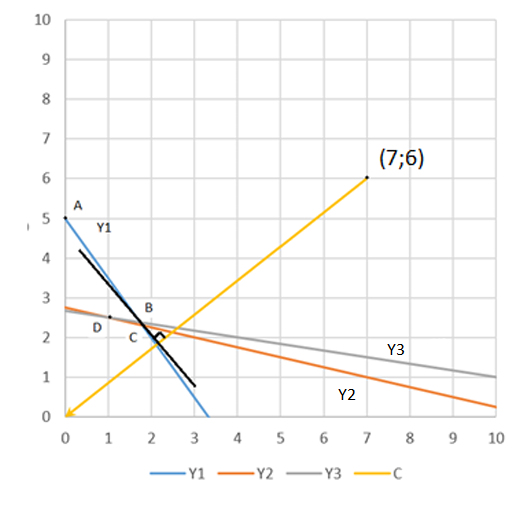
Решение:

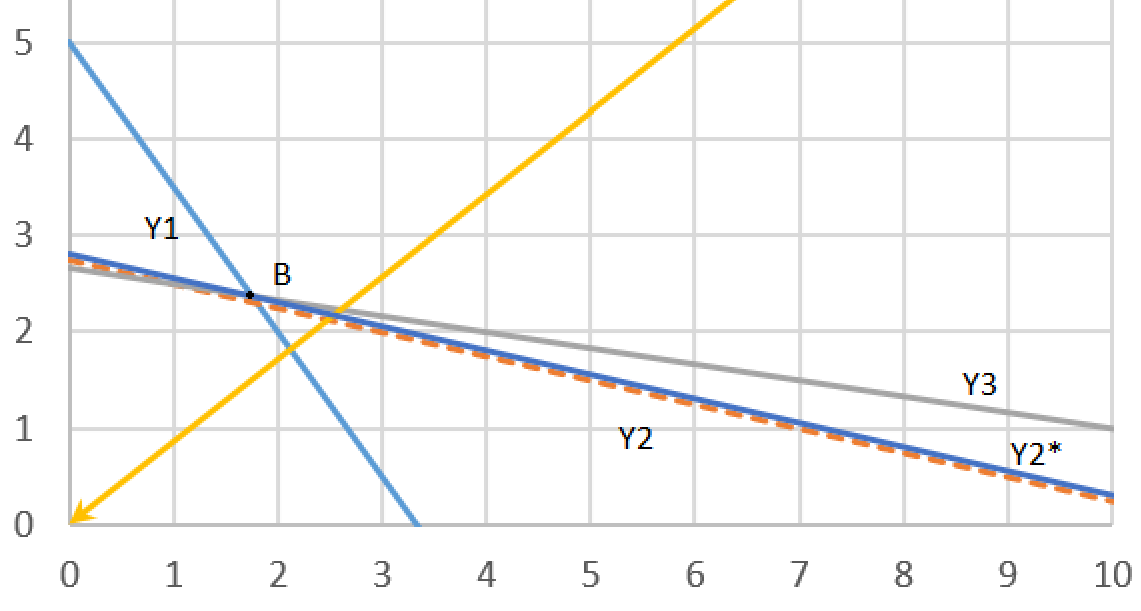
Точка B имеет координаты (1,76; 2,37)

Подставим их в целевую функцию и найдем ее значение

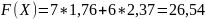
Ответ: Дневной рацион, имеющий минимальную стоимость, составляет 1,76 ед первого корма, и 2,37 единицы 2 корма, стоимость корма 26,54 д.e.

Анализ чувствительности.

Анализ запасов сырья А.

Прямая y₁ соответствует дефицитному ресурсу, так как является связывающим ограничением (проходит через точку оптимума).

Дефицитный ресурс можно увеличить, то есть передвинуть прямую у₂ до точки G, в которой она становится избыточной.

Теперь ОДЗ расширилось и стало GDE.

Новая точка оптимума точка G. Координаты точки G (0; 2,75).

Найдем значение целевой функции в новой точке.

F (G)  7  0  6  2,75  16,5

Найдем новое неравенство для ресурса A.

Старое неравенство:

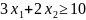
Подставим точку G, которая принадлежит новой прямой у₂ , в левую часть неравенства.

Координаты точки G (0; 2,75)

Новое неравенство:

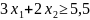
Рисунок 3 – График смещения прямой у₁

Рисунок 4 – ОДЗ с новой прямой y1

Анализ запасов сырья B.

Прямая y₃ соответствует недефицитному ресурсу, так как является избыточным ограничением (если исключить это ограничение – ОДЗ не изменится).

Недефицитный ресурс можно увеличить, то есть передвинуть прямую у₁ до точки оптимума В.

В результате передвижения ОДЗ не изменилось, и точка оптимума осталась прежней.

Координаты точки В: (1,76; 2,37).

Значение целевой:

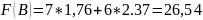
Найдем новое неравенство для ресурса С.

Старое неравенство:

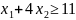
Подставим точку B, которая принадлежит новой прямой у₂, в левую часть неравенства.

Новое неравенство:

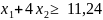
Рисунок 3 – График смещения прямой у₂

Анализ запасов сырья C.

Прямая y₃ соответствует дефицитному ресурсу, так как является связывающим ограничением (проходит через точку оптимума).

Дефицитный ресурс можно увеличить, то есть передвинуть прямую у₃ до точки H, в которой она становится избыточной.

Теперь ОДЗ расширилось и стало ACH.

Новая точка оптимума точка С. Найдем координаты точки С. Для этого приравняем уравнения прямых Y1 и Y2

Найдем значение целевой функции в новой точке.

Найдем новое неравенство для ресурса C.

Старое неравенство:

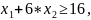
Подставим точку H, которая принадлежит новой прямой у₃, в левую часть неравенства.

Координаты точки H (11; 0)

Новое неравенство:

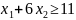
Рисунок 5 – График смещения прямой у₃

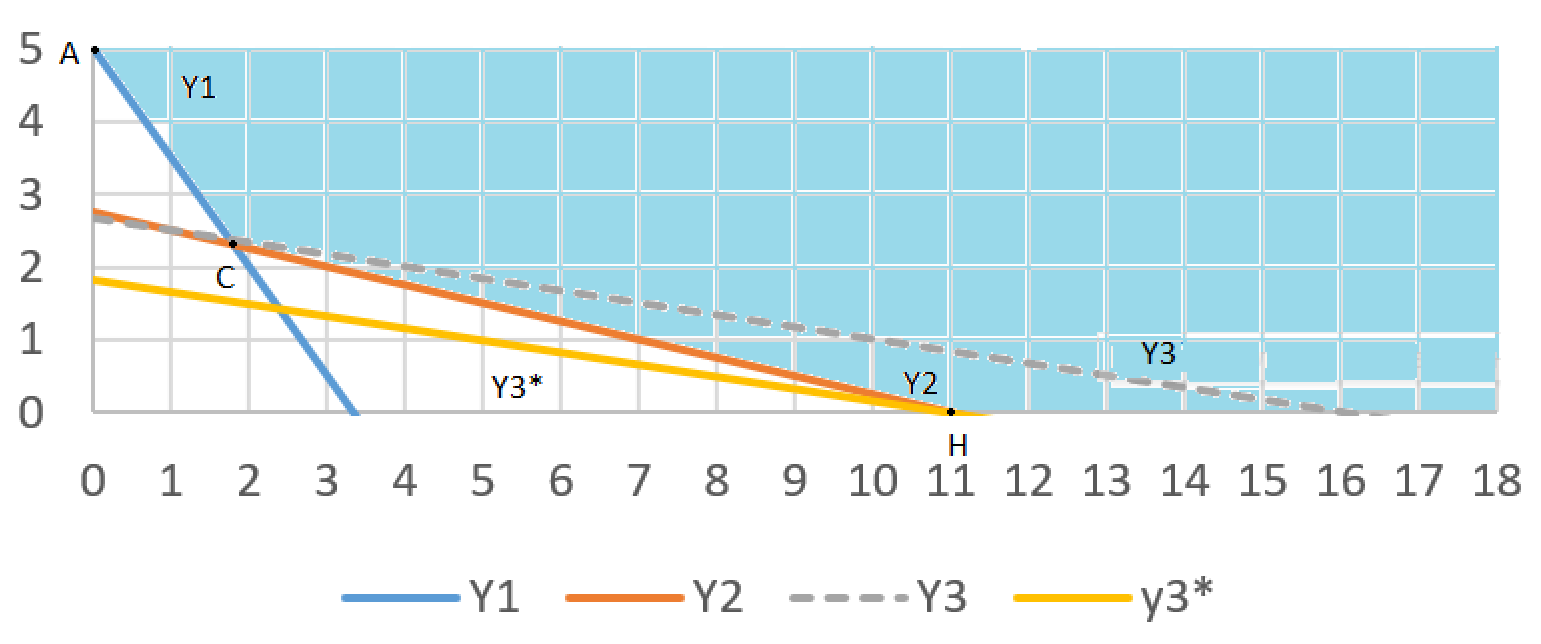
Рисунок 6 – ОДЗ с новой прямой у₃

Результирующая таблица. Расчет теневой цены.

Ресурс	Тип ресурса	Максимальное изменение запасов ресурсов	Максимальное уменьшение стоимости от изменений
А	Дефицитный	5,5 – 10 = -4,5	16,5 – 26,54 = -10,04
В	Недефицитный	11,24 – 11 = +0,24	26,54 – 26,54 = 0
С	Дефицитный	11 – 16 = -5	26,4 – 26,54 = -0,14

В результате можно увидеть, что при изменении ресурса A, стоимость будет уменьшатся значительнее. Закупив запас ресурса А на 4,5 единиц меньше, стоимость уменьшится на 10,04 денежных единиц.