
ЛР2_Саляхов_ИВТ-429Б
.docxФедеральное бюджетное государственное образовательное учреждение высшего образования
Уфимский университет науки и технологий
Кафедра АСУ
Отчет по лабораторной работе №2
по дисциплине «Интеллектуальные информационные системы»
по теме «Применение нейронных сетей для решения задач классификации, аппроксимации функции и прогнозирования с помощью аналитического пакета Deductor»
Выполнил: ст. гр. ИВТ-429Б
Саляхов А.Ф.
Проверил:
Алыпов Ю.Е.
Уфа – 2024
Цель:
Целью работы является исследование процедуры работы с аналитическим пакетом Deductor при решении задач классификации, аппроксимации функции и прогнозирования.
Ход работы:
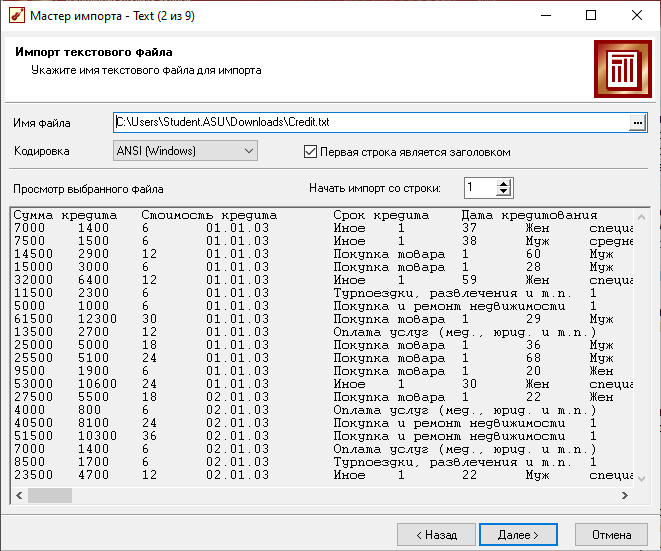
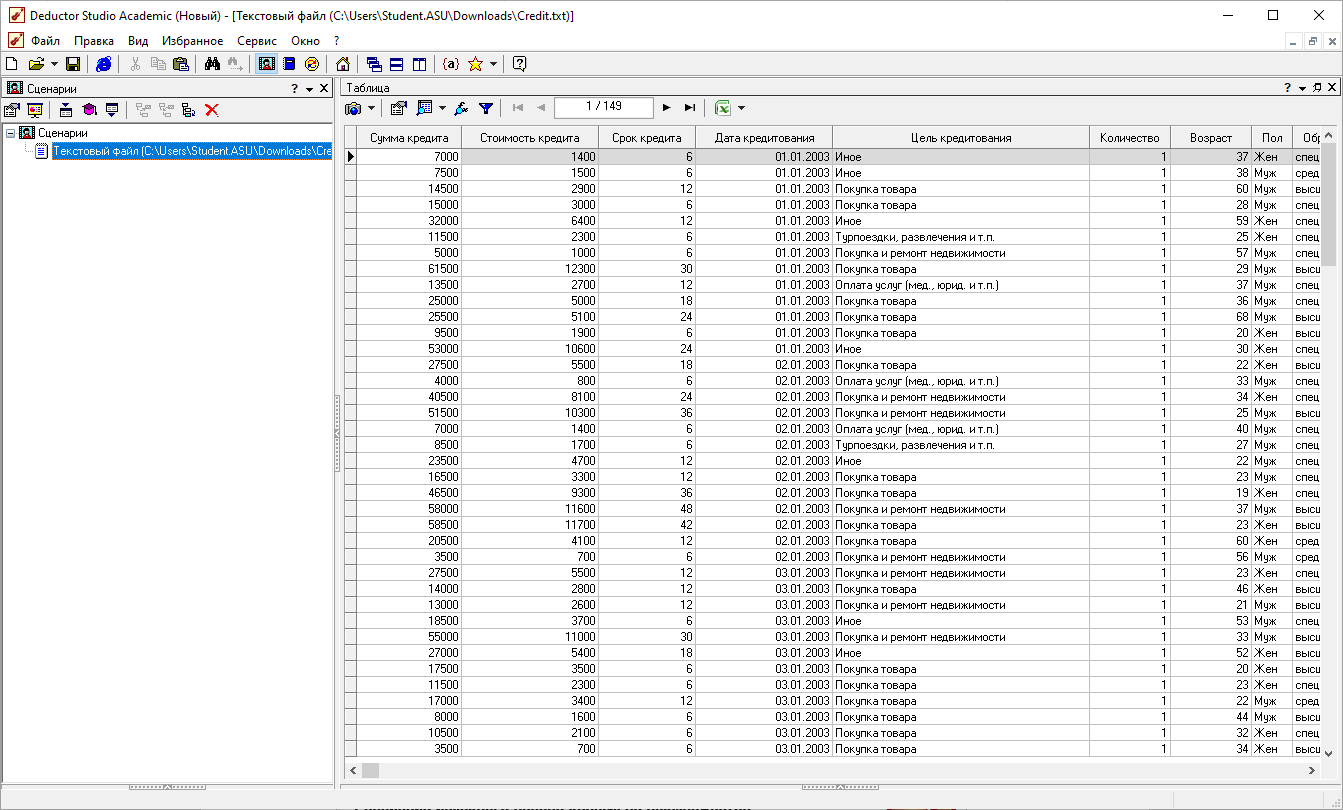
Импортировали
данные из файла при помощи Мастера
импорта
Классификация
Мастер обработки
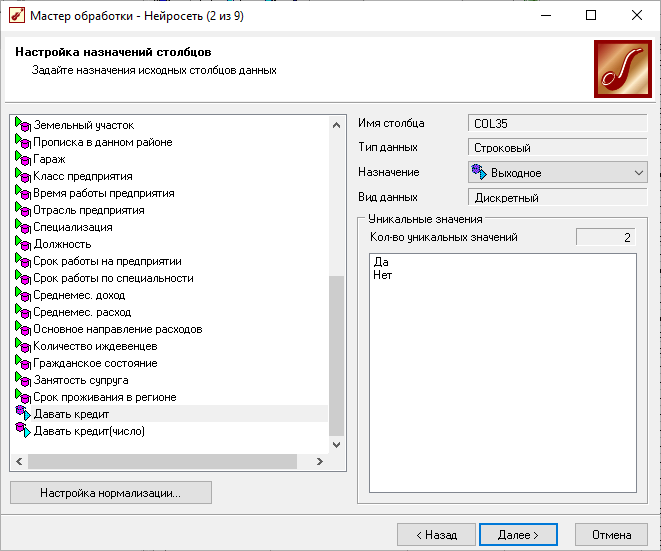
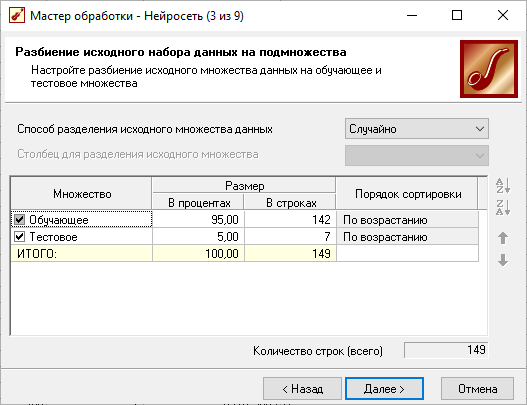


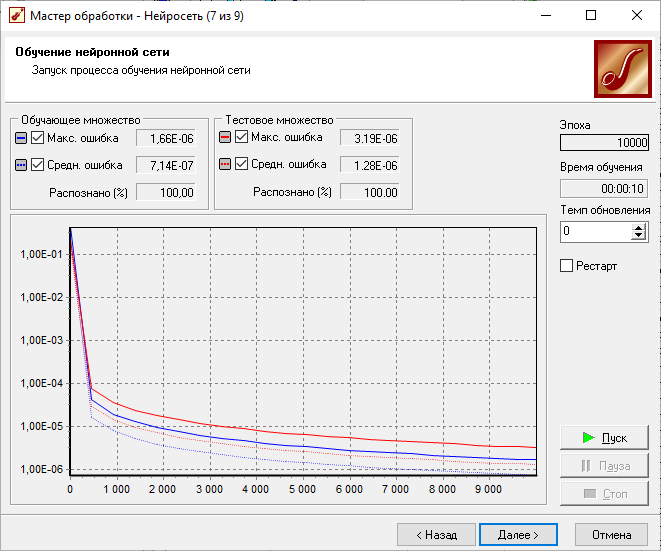
Полученные данные
Граф
нейросети
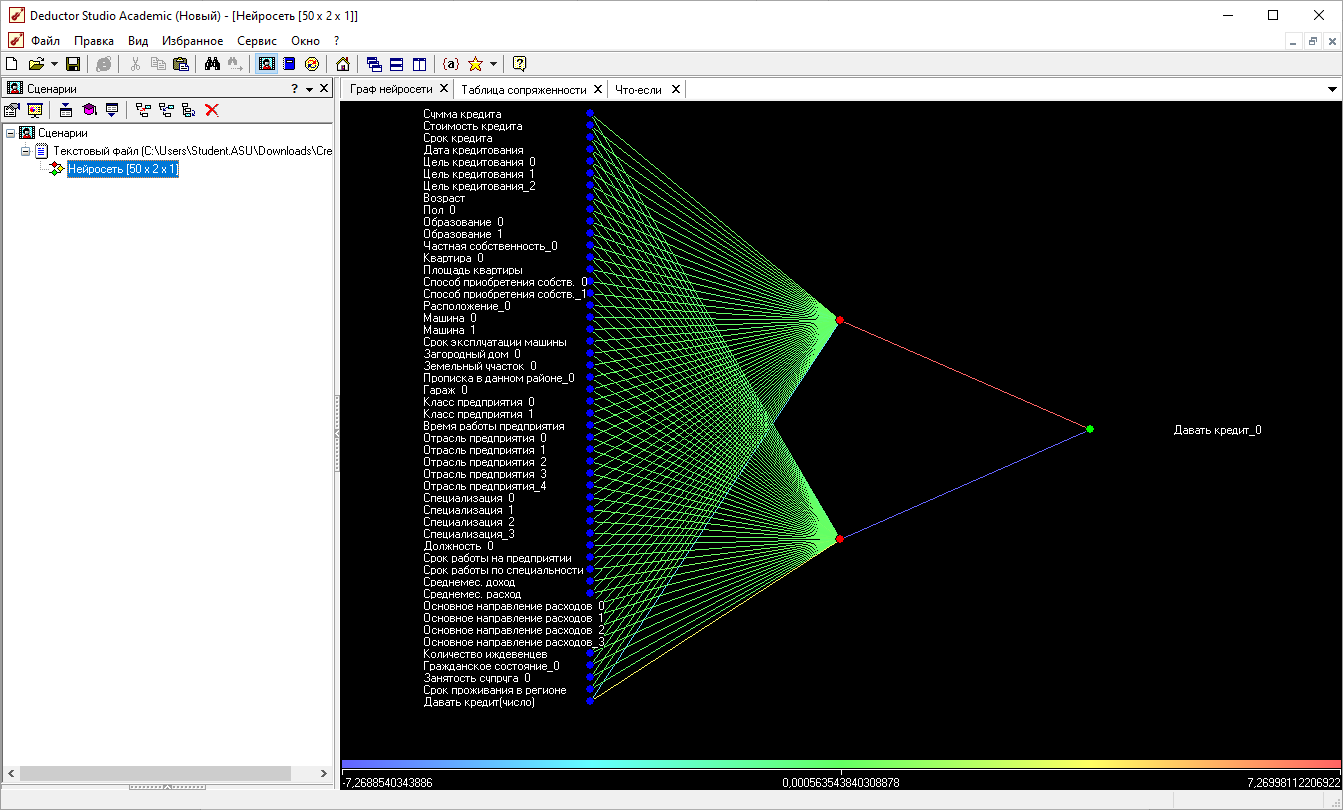
Таблица сопряженности

Что-то если
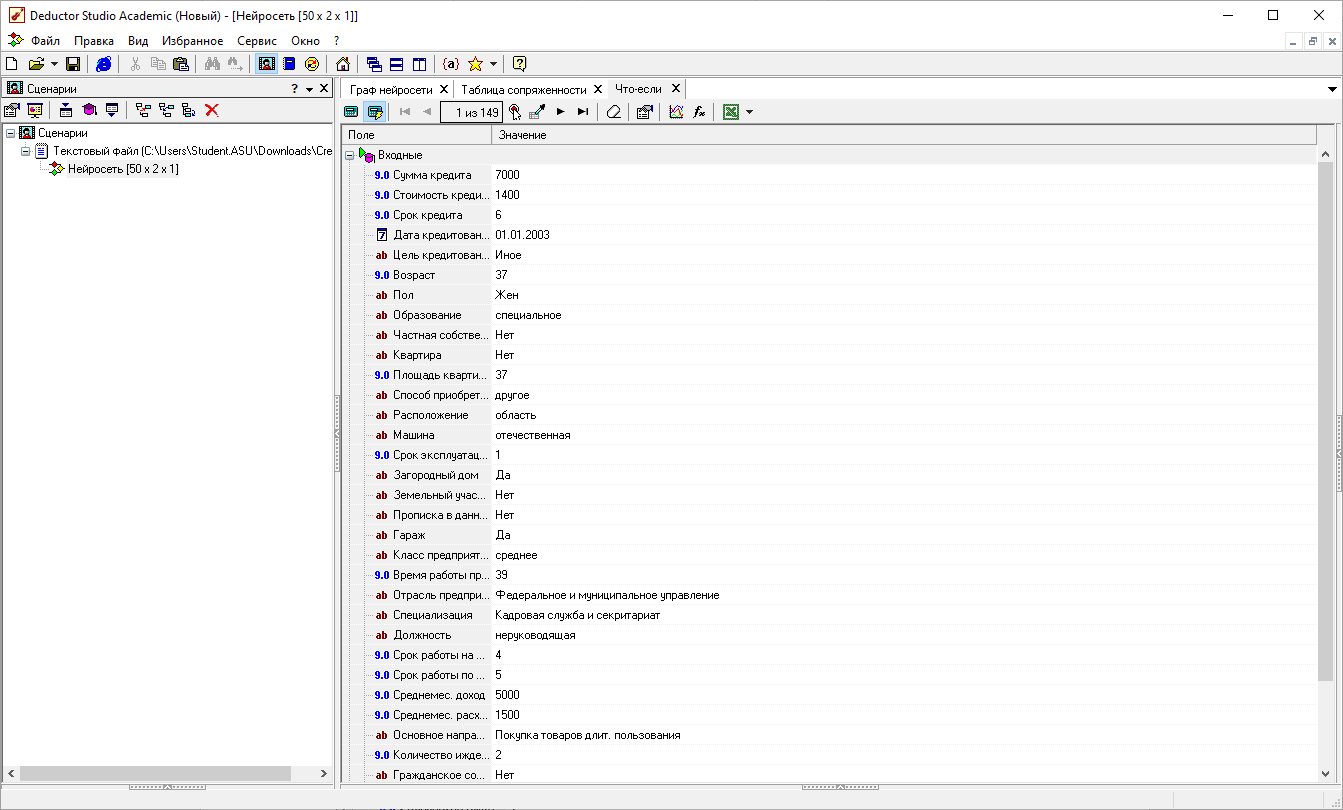
Задача классификации
Структура НС (описание входов и выходов)
Содержание обучающей выборки.
Результаты обучения НС
Результаты опроса нейронной сети.
Задача аппроксимации
Структура НС (описание входов и выходов)
Функция: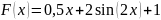 .
Ограничим диапазон до [π/2, π].
.
Ограничим диапазон до [π/2, π].
Будем использовать 1 скрытый слой с 5-ю нейронами. 1 входной и 1 выходной нейроны.
Содержание обучающей выборки.
x
F(x)
0,039
0,992472
0,078
0,970781
0,117
0,937435
0,156
0,896093
0,195
0,85095
0,234
0,806174
0,273
0,76549
0,312
0,731995
0,351
0,708176
0,39
0,696077
0,429
0,697537
0,468
0,714451
0,507
0,748993
0,546
0,803773
0,585
0,881863
0,624
0,986618
0,663
1,121194
0,702
1,28764
0,741
1,485492
0,785398
1,742569
Результаты обучения НС
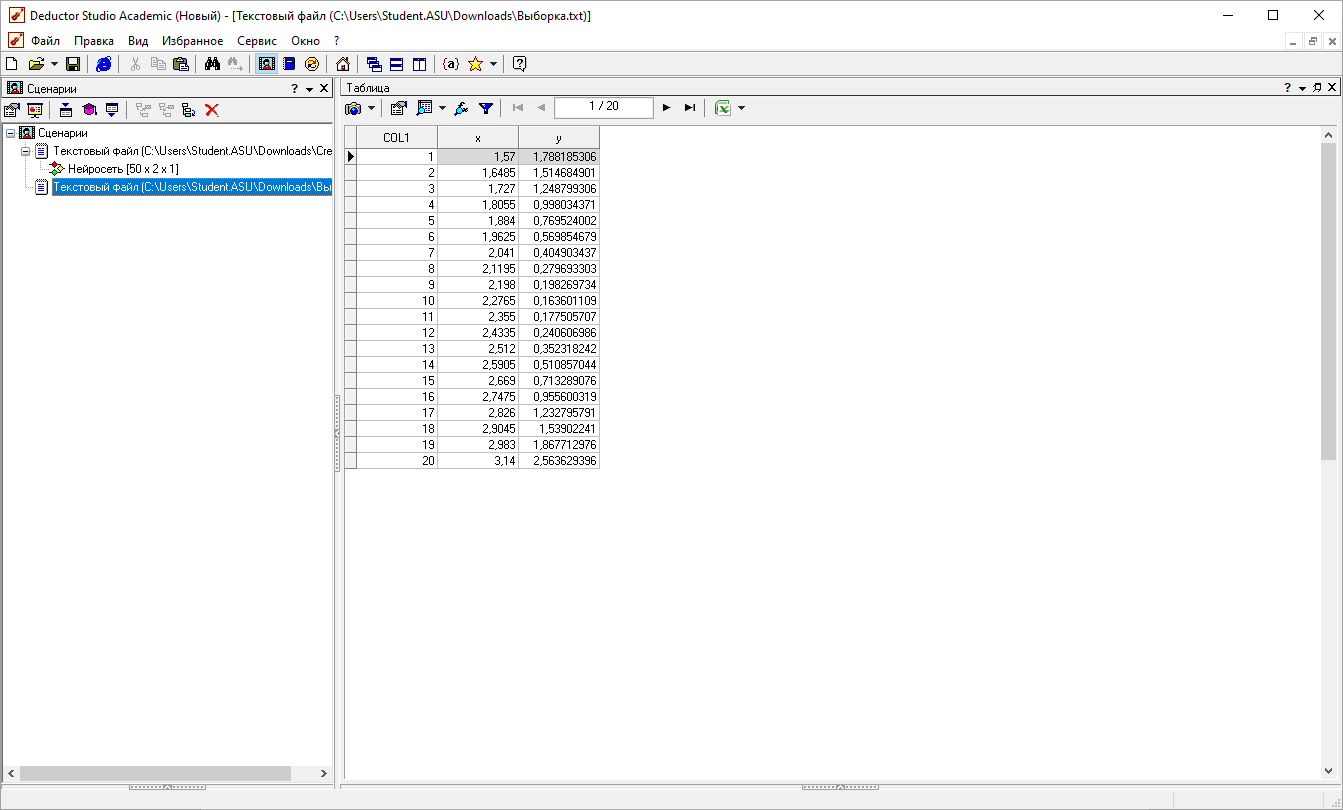
Импорт выборки
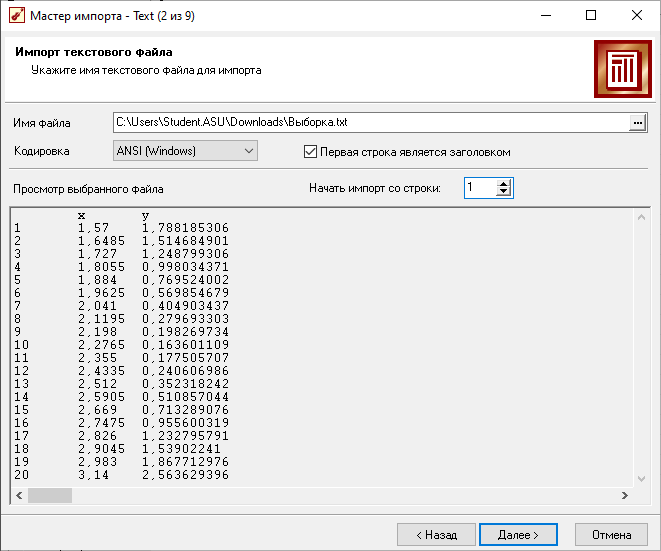
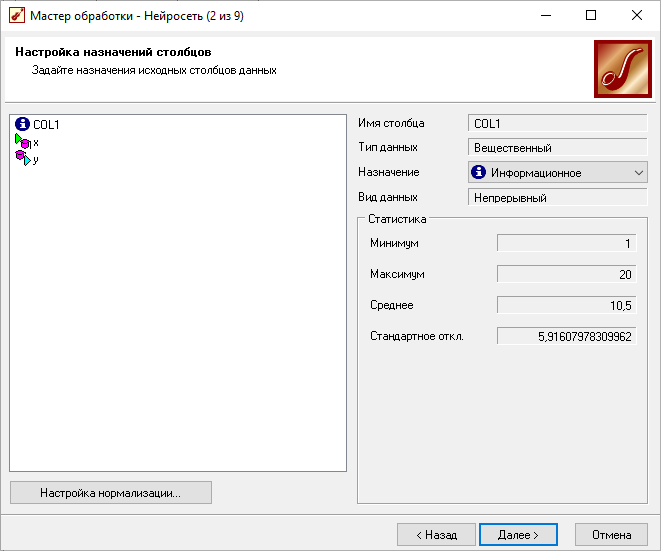
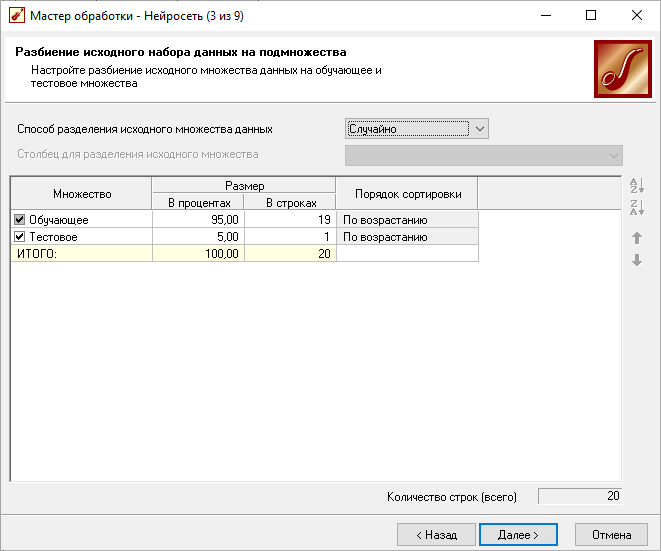
Настройка НС
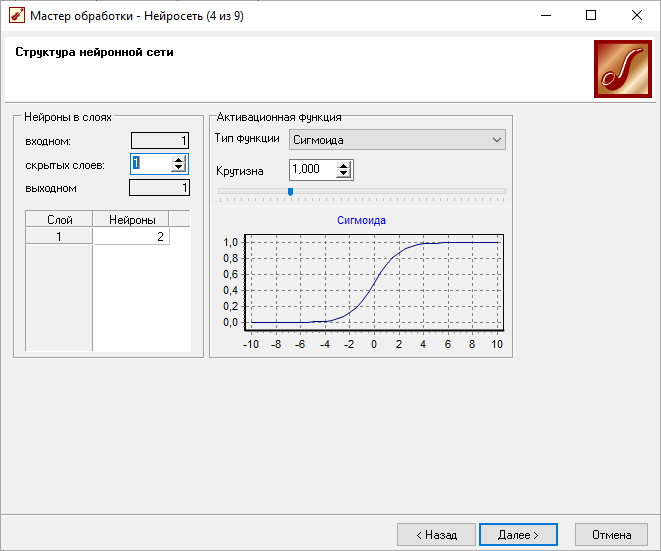

Обучение

Граф сети
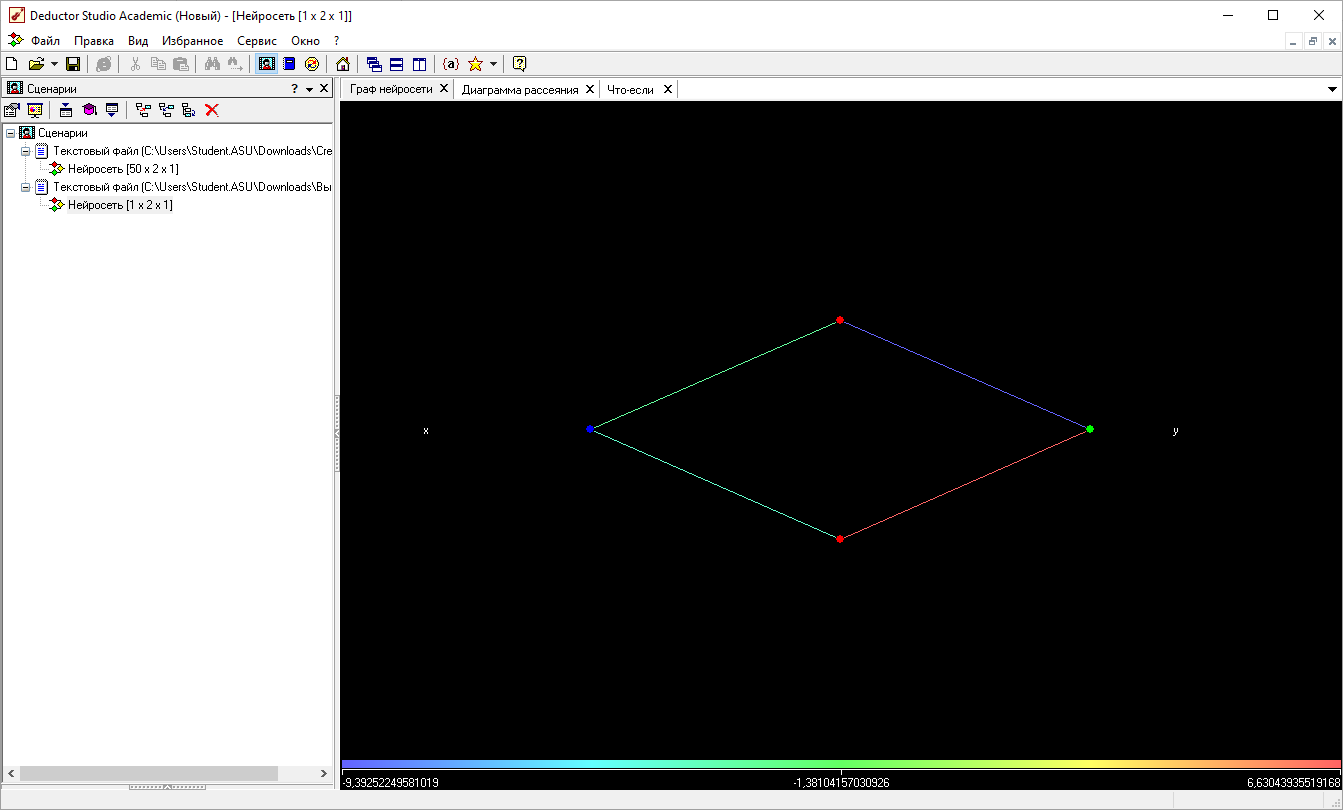
Результаты опроса нейронной сети.
Анализ в мастере визуализации «Что-Если»
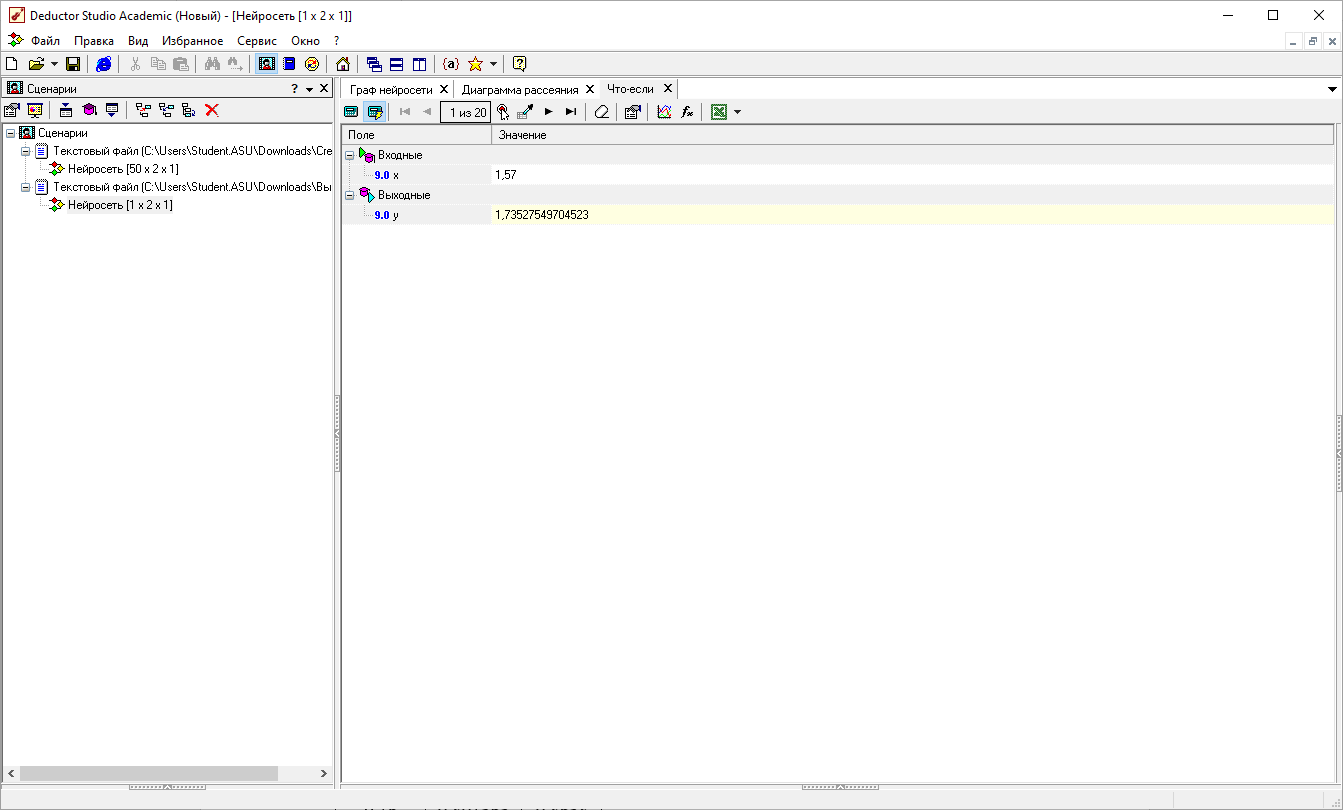
X |
Истинное |
НС |
1,57 |
1,788185 |
1,735275 |
1,727 |
1,248799 |
1,300882 |
1,884 |
0,769524 |
0,726966 |
2,041 |
0,404903 |
0,385441 |
2,198 |
0,19827 |
0,281103 |
2,355 |
0,177506 |
0,275965 |
2,512 |
0,352318 |
0,352775 |
2,669 |
0,713289 |
0,621231 |
2,826 |
1,232796 |
1,252354 |
2,983 |
1,867713 |
1,950685 |
Средняя ошибка 0,01294 или ~1,3%, что меньше заданной 0,05. Аппроксимация функции достаточно точная.
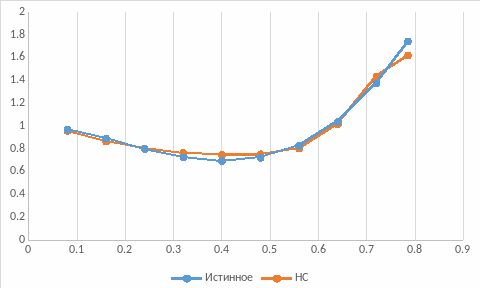
Задача прогнозирования
Структура НС (описание входов и выходов)
Будем использовать НС с одним скрытым слоем. Число входных нейронов - 12, число выходных нейронов - 1. Число нейронов в скрытом слое равно 2.
Содержание обучающей выборки.
Импорт выборки

Выборка
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
X11 |
X12 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
2 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
2 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
2 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
2 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
2 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
2 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
2 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
2 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
2 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
Создание НС
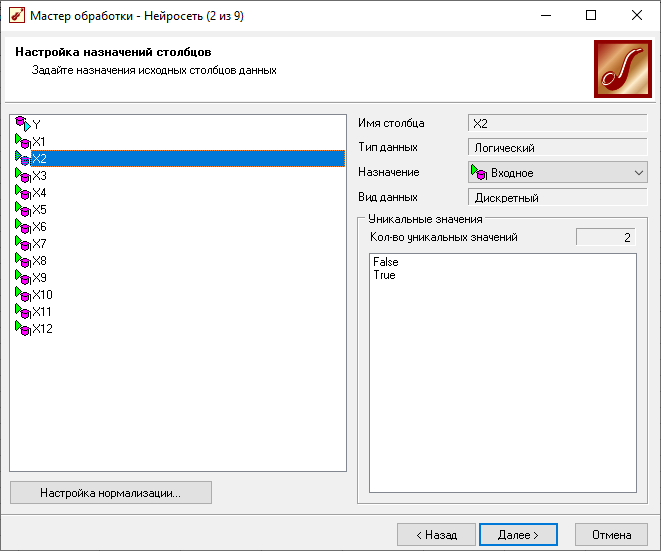
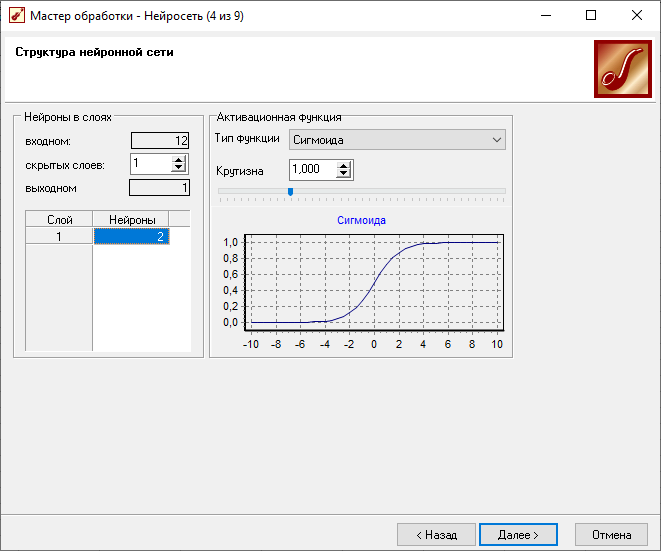
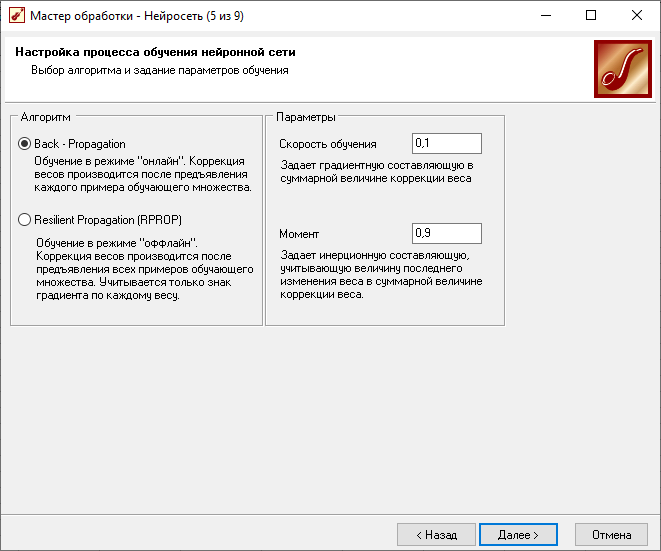
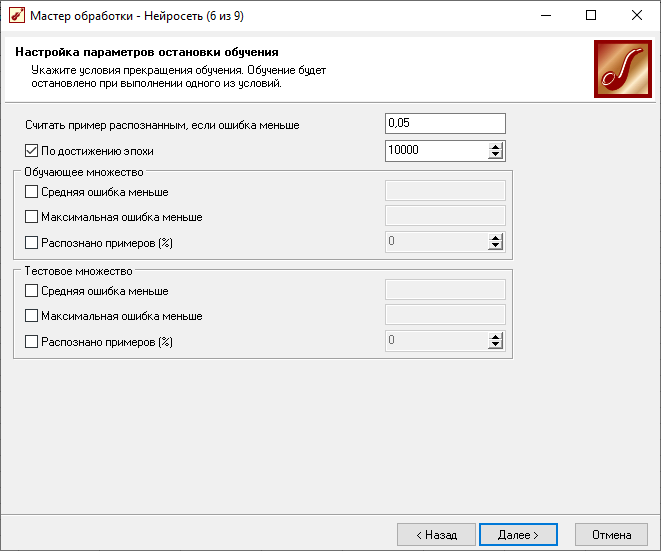
Результаты обучения НС
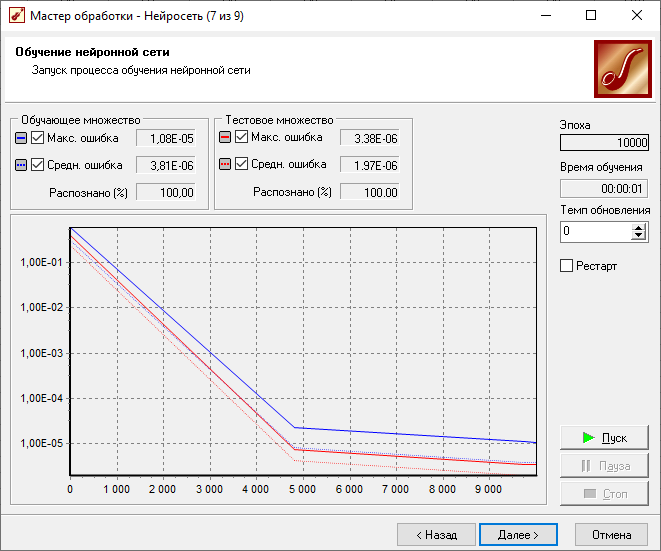
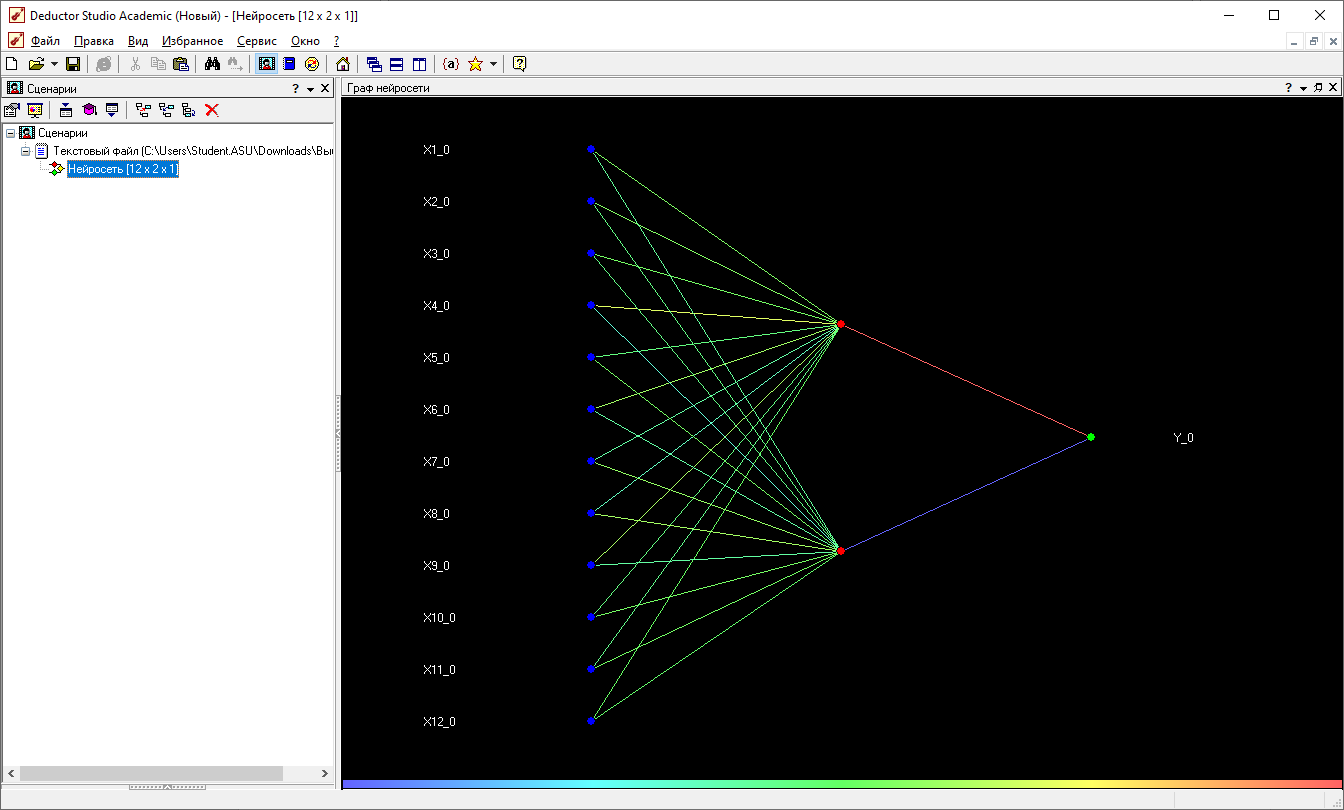
Результаты опроса нейронной сети.
Импорт тестового множества
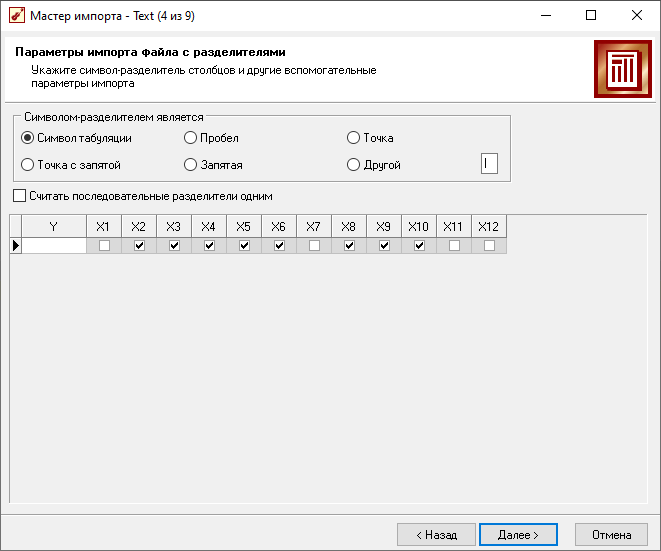
Результаты опроса

Как видим, Y максимально близок к значению 2, т.е. сеть прогнозирует победу кандидата от оппозиционной партии
Вывод
В ходе данной лабораторной работы были исследованы процедуры работы с аналитическим пакетом Deductor при решении задач классификации, аппроксимации функции и прогнозирования.
