ЛР1_Саляхов_ИВТ-429Б

ФГБОУ ВО

Уфимский университет науки и технологии

Кафедра АСУ

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1

По дисциплине

«Интеллектуальные информационные системы»

На тему:

«Применение нейронных сетей для аппроксимации неизвестных функций. Идентификация черного ящика»

Выполнили:

студент группы ПИ-429Б

Саляхов А.Ф.

Проверил:

доцент кафедры АСУ

Алыпов Ю. Е.

Уфа 2024

Функция 7 варианта и 2 диапазона:

1 диапазон:

В текстовом файле «выборка» перечисляем числа, входящие в диапазон

Рис.1.

Выбираем текстовый файл в Neural Network Wizard (рис.2)

Рис.2.

В новом окне (рис.3) видим список доступных полей и их параметры нормализации.

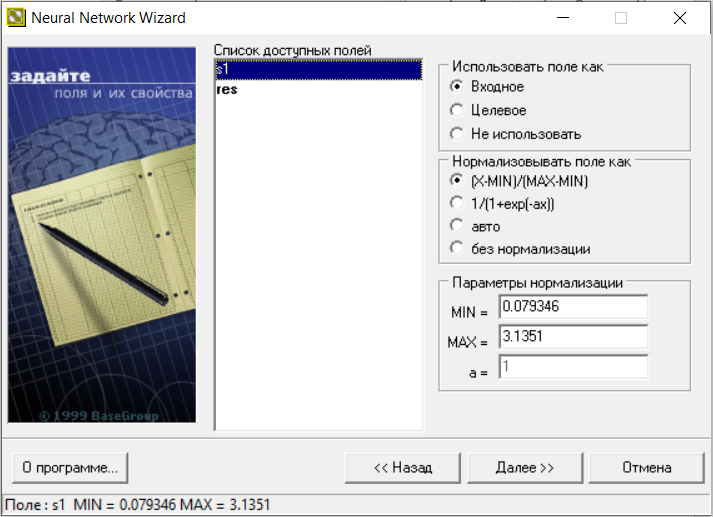
Рис.3

В следующем окне (рис.4) меняем число нейронов на 3.

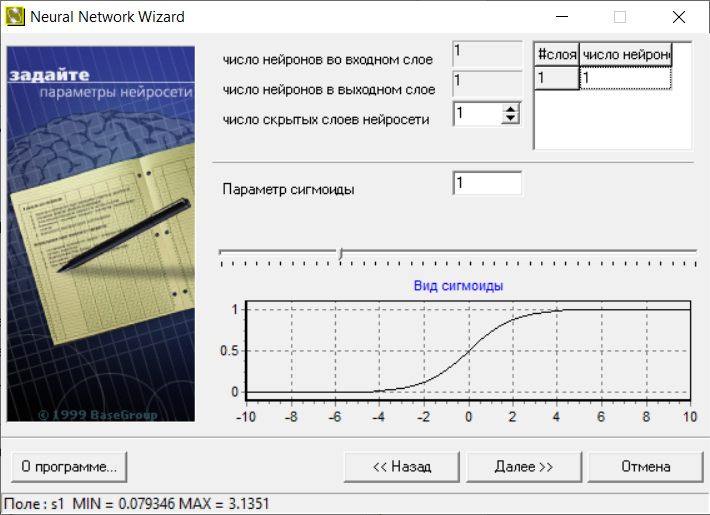
Рис.4

В следующем окне визуализирован процесс обучения (рис. 5). На верхней диаграмме показано распределение ошибки обучения: по горизонтали значение ошибки (чем правее столбец, тем больше ошибка), по вертикали количество примеров из выборки с данной ошибкой.

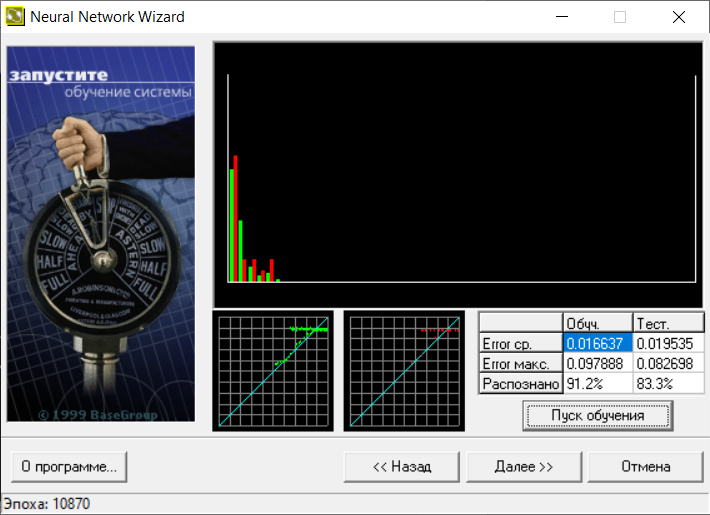
Рис.5

Оцениваем точность работы НС в эксплуатационном режиме, рассчитываем произвольное значение входного сигнала. По этим значениям строим диаграмму и сравниваем с диаграммой функции.

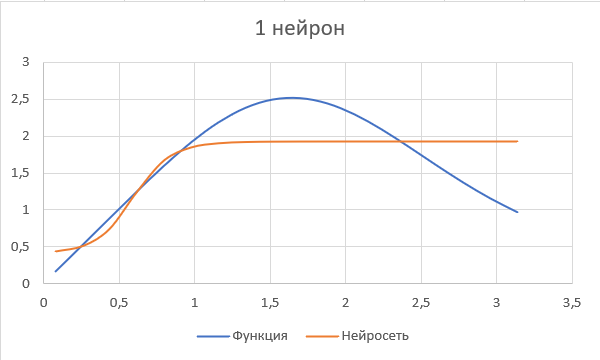
Рис.6

В следующем окне (рис.7) меняем число нейронов на 3.

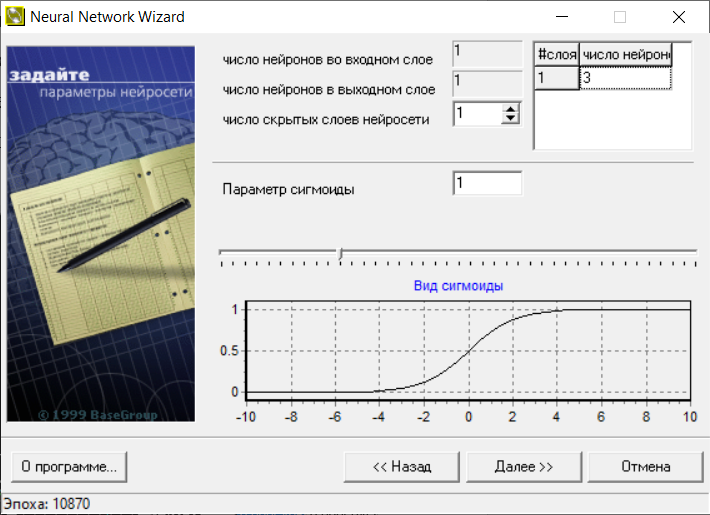
Рис.7

В следующем окне визуализирован процесс обучения (рис. 8). На верхней диаграмме показано распределение ошибки обучения: по горизонтали значение ошибки (чем правее столбец, тем больше ошибка), по вертикали количество примеров из выборки с данной ошибкой.

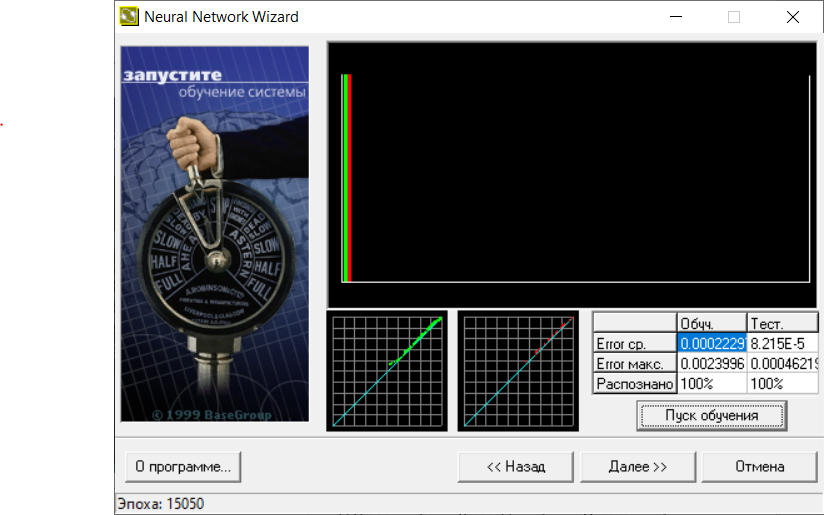
Рис.8

Оцениваем точность работы НС в эксплуатационном режиме, рассчитываем произвольное значение входного сигнала. По этим значениям строим диаграмму и сравниваем с диаграммой функции (рис.9).

Рис.9

В следующем окне (рис.10) меняем число нейронов на 5.

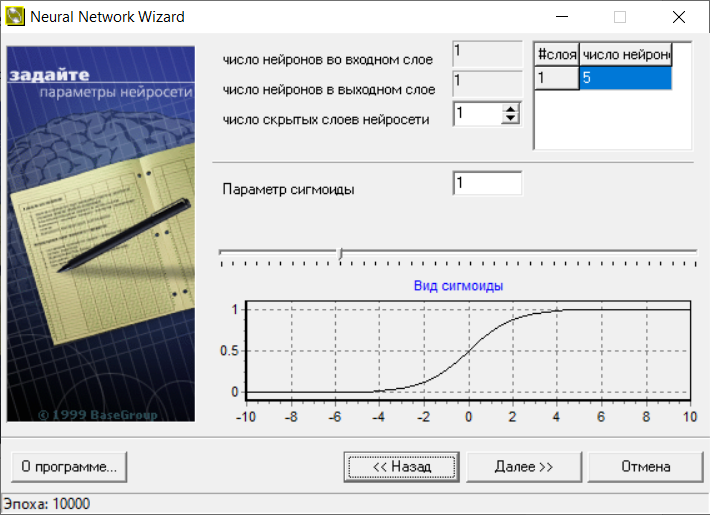
Рис.10

В следующем окне визуализирован процесс обучения (рис. 11). На верхней диаграмме показано распределение ошибки обучения: по горизонтали значение ошибки (чем правее столбец, тем больше ошибка), по вертикали количество примеров из выборки с данной ошибкой.

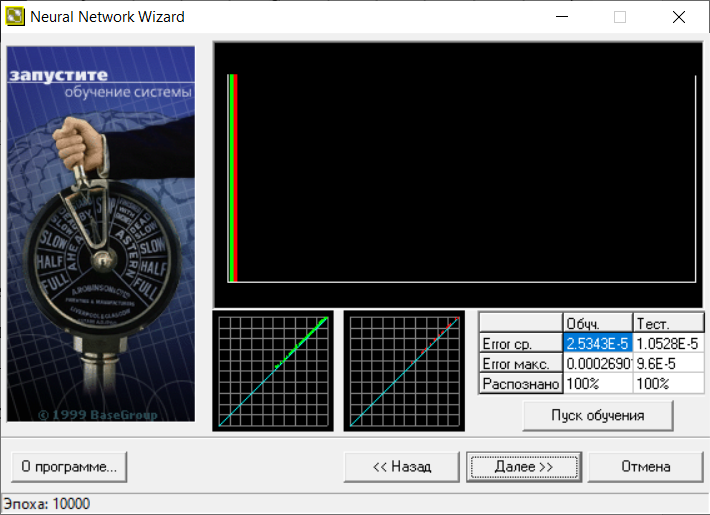
Рис.11

Оцениваем точность работы НС в эксплуатационном режиме, рассчитываем произвольное значение входного сигнала. По этим значениям строим диаграмму и сравниваем с диаграммой функции (рис.12).

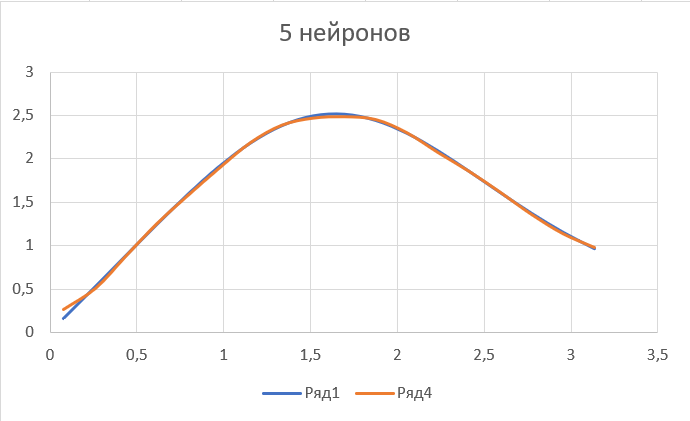
Рис.12

В следующем окне (рис.13) меняем число нейронов на 7.

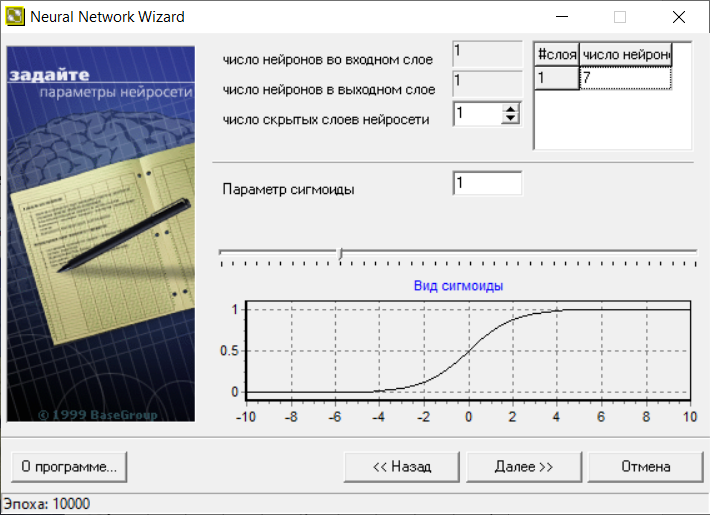
Рис.13

В следующем окне визуализирован процесс обучения (рис. 14). На верхней диаграмме показано распределение ошибки обучения: по горизонтали значение ошибки (чем правее столбец, тем больше ошибка), по вертикали количество примеров из выборки с данной ошибкой.

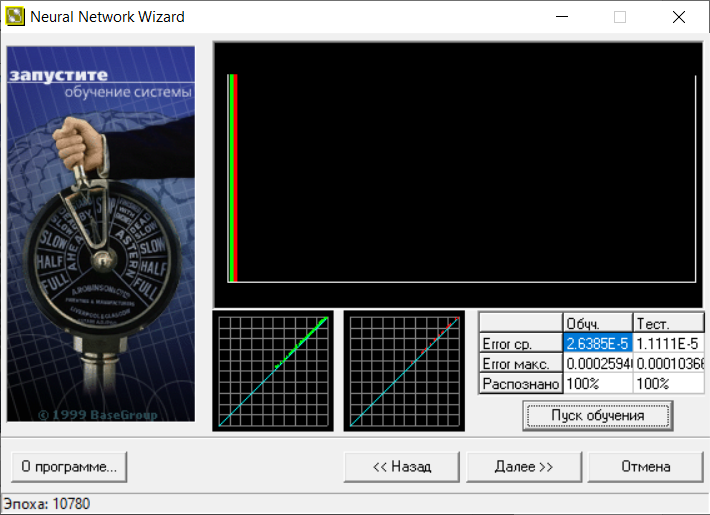
Рис.14

Оцениваем точность работы НС в эксплуатационном режиме, рассчитываем произвольное значение входного сигнала. По этим значениям строим диаграмму и сравниваем с диаграммой функции (рис.15).

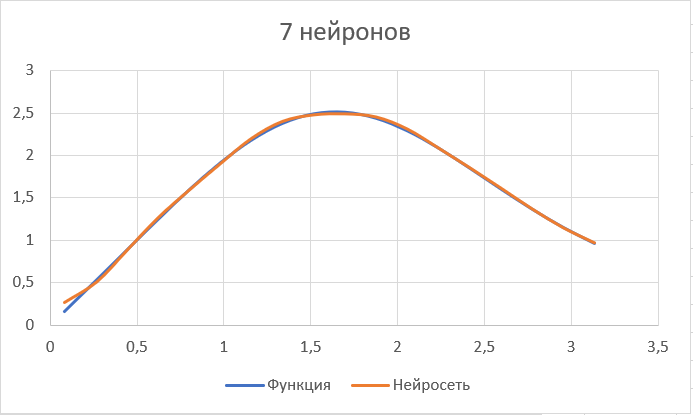
Рис.15

2 диапазон:

В текстовом файле «выборка» перечисляем числа, входящие в диапазон

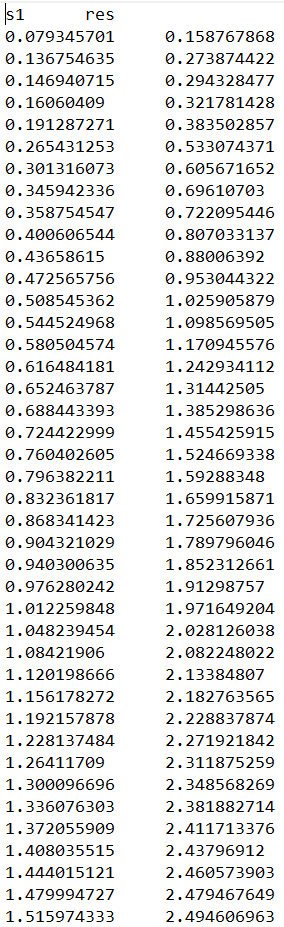
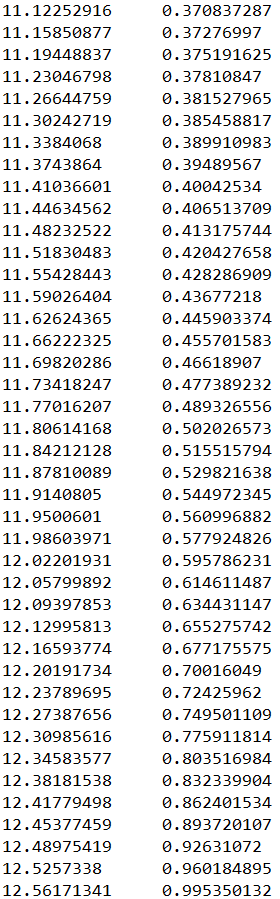
Рис.16.

Выбираем текстовый файл в Neural Network Wizard (рис.17)

Рис.17.

В новом окне (рис.18) видим список доступных полей и их параметры нормализации.

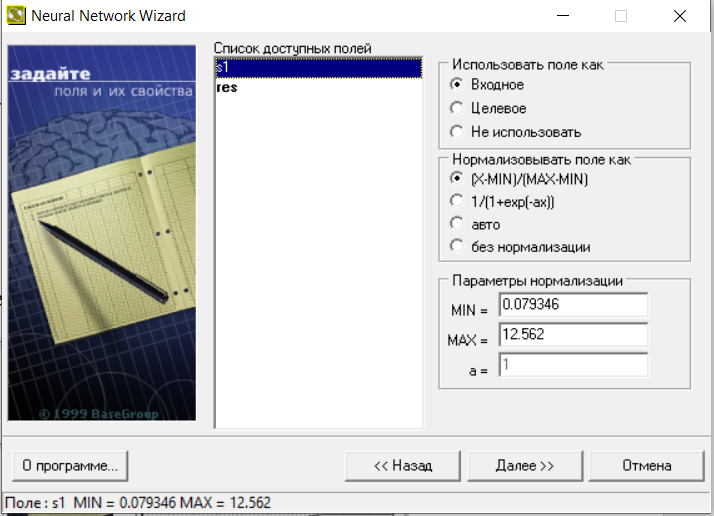
Рис.18.

В следующем окне (рис.19) устанавливаем число нейронов 1.

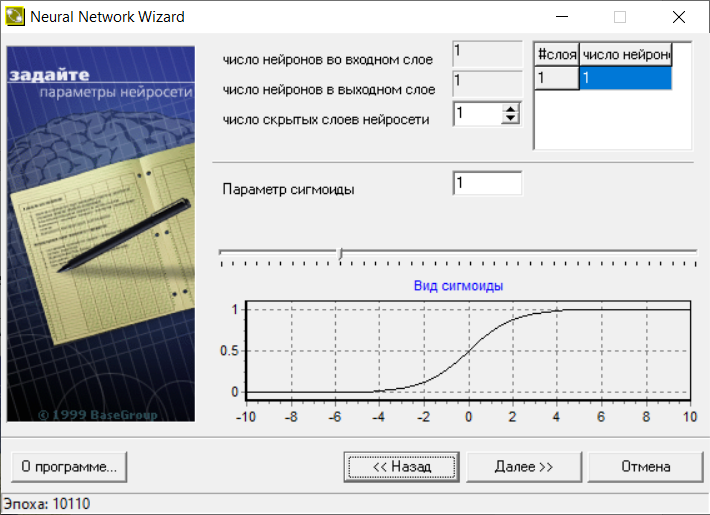
Рис.19.

В следующем окне визуализирован процесс обучения (рис. 20). На верхней диаграмме показано распределение ошибки обучения: по горизонтали значение ошибки (чем правее столбец, тем больше ошибка), по вертикали количество примеров из выборки с данной ошибкой.

Рис.20.

Оцениваем точность работы НС в эксплуатационном режиме, рассчитываем произвольное значение входного сигнала. По этим значениям строим диаграмму и сравниваем с диаграммой функции.

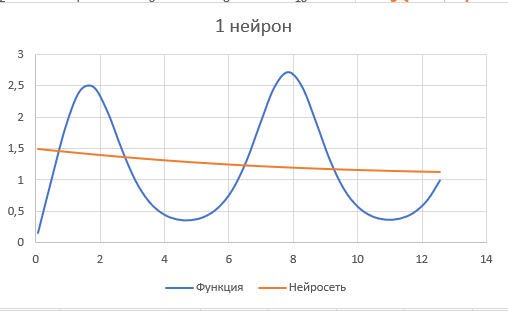
Рис.21.

В следующем окне (рис.19) меняем число нейронов на 3.

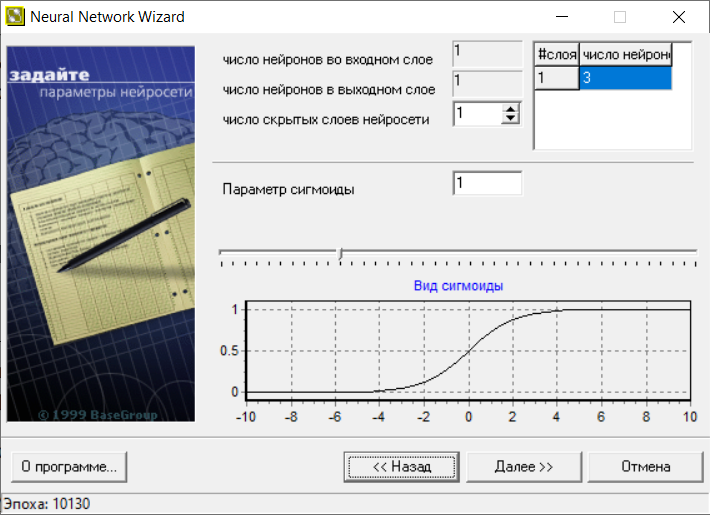
Рис.19.

В следующем окне визуализирован процесс обучения (рис. 20). На верхней диаграмме показано распределение ошибки обучения: по горизонтали значение ошибки (чем правее столбец, тем больше ошибка), по вертикали количество примеров из выборки с данной ошибкой.

Рис.20.

Оцениваем точность работы НС в эксплуатационном режиме, рассчитываем произвольное значение входного сигнала. По этим значениям строим диаграмму и сравниваем с диаграммой функции.

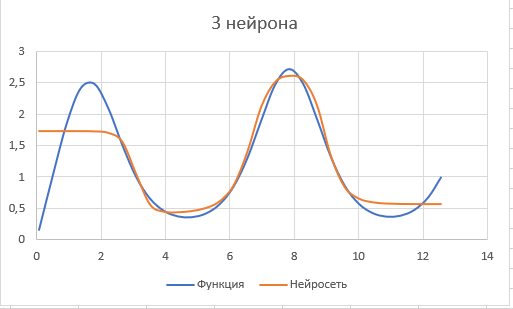
Рис.21.

В следующем окне (рис.22) меняем число нейронов на 5.

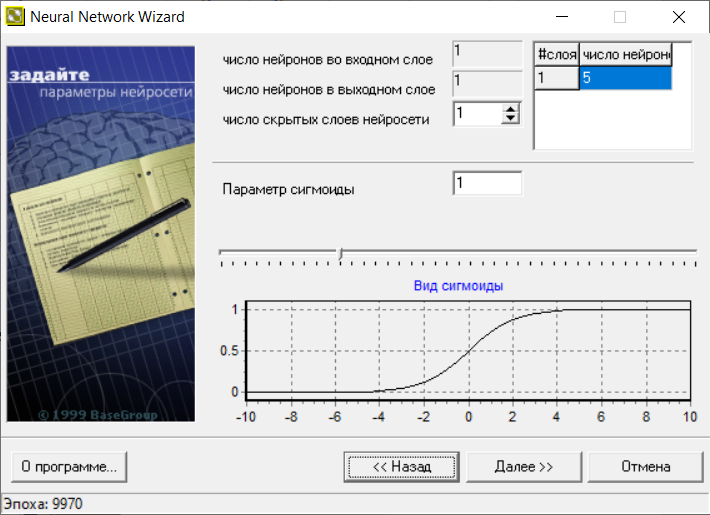
Рис.22.

В следующем окне визуализирован процесс обучения (рис. 23). На верхней диаграмме показано распределение ошибки обучения: по горизонтали значение ошибки (чем правее столбец, тем больше ошибка), по вертикали количество примеров из выборки с данной ошибкой.

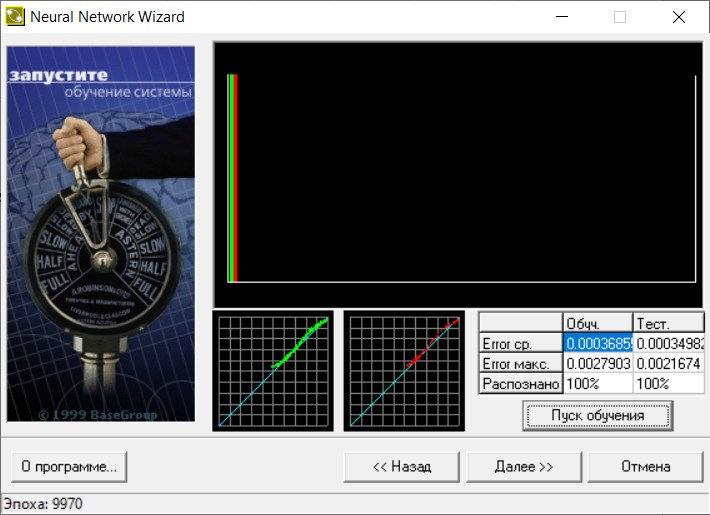
Рис.23.

Оцениваем точность работы НС в эксплуатационном режиме, рассчитываем произвольное значение входного сигнала. По этим значениям строим диаграмму и сравниваем с диаграммой функции.

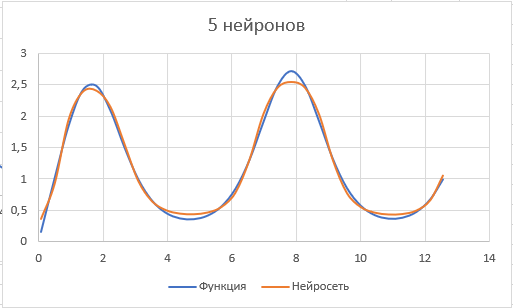
Рис. 24.

В следующем окне (рис.25) меняем число нейронов на 7.

Рис.25.

В следующем окне визуализирован процесс обучения (рис.26). На верхней диаграмме показано распределение ошибки обучения: по горизонтали значение ошибки (чем правее столбец, тем больше ошибка), по вертикали количество примеров из выборки с данной ошибкой.

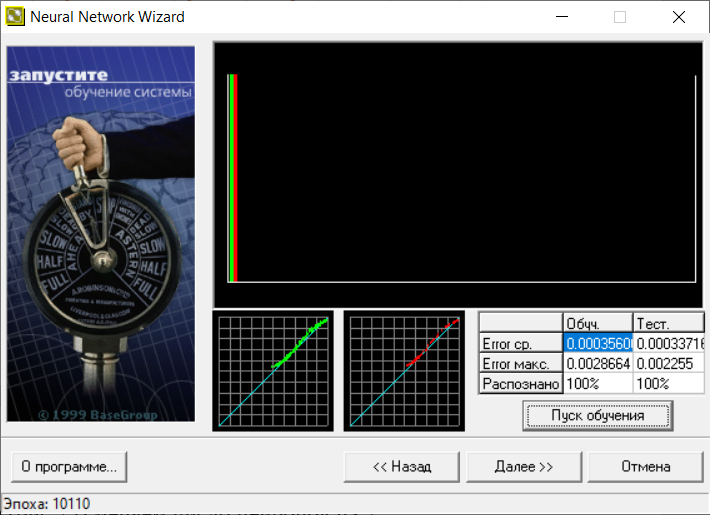
Рис.26.

Оцениваем точность работы НС в эксплуатационном режиме, рассчитываем произвольное значение входного сигнала. По этим значениям строим диаграмму и сравниваем с диаграммой функции.

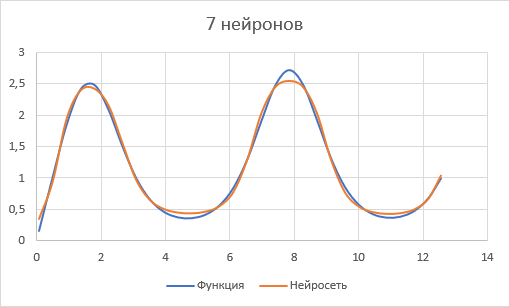
Рис.24.

Вывод: в ходе выполнения лабораторной работы выполнили аппроксимацию функции с помощью нейросети в заданном диапазоне. Проводили обучение нескольких нейронных сетей c помощью нейроимитатора Neural Network Wizard с количеством нейронов в скрытом слое, равном 1, 3, 5, 7 и функцией активации «сигмоидная». Проверили качество каждой обученной сети, для чего рассчитали значения выходной переменной по заданной функции и по нейронной сети, затем на графике показали близость каждой обученной модели к исходной. На графиках видно, что между качеством обучения нейросети и количеством нейронов в скрытом слое есть прямая зависимость.