
- •События. Действия над событиями.
- •Классическая вероятность. Свойства вероятностей.
- •Основные правила комбинаторики. Сочетания, размещения, выбор без возвращения и с возвращением
- •Дискретная вероятность и ее свойства.
- •Общее определение вероятности (аксиоматика Колмогорова). Свойства вероятностей.
- •Условная вероятность и ее свойства.
- •Независимость событий. Свойства независимых событий.
- •Пример Бернштейна. Независимость n событий.
- •Теорема Бернулли.
- •Локальная и интегральная предельные теоремы Муавра - Лапласа.
- •Теорема Пуассона.
- •Случайные величины. Функции распределения случайных величин. Характеризационные свойства функций распределения.
- •Функции распределения дискретного типа. Примеры.
- •Функции распределения абсолютно непрерывного типа. Плотность распределения. Примеры.
- •Математическое ожидание. Примеры вычисления математического ожидания.
- •Свойства математического ожидания.
- •Квантили. Вариационный ряд.
- •Метод моментов. Выборочный метод.
- •Метод максимального правдоподобия
- •Оценки параметров линейной регрессии
- •Проверка статистических гипотез. Общие положения. Ошибки первого и второго рода
- •Критерий Неймана–Пирсона. Критерий проверки гипотезы о среднем значении нор- мальной генеральной совокупности с известной дисперсией.
- •Критерий Пирсона
- •Критерий Колмогорова
Событие – явление, которое может произойти или не произойти при осуществлении определённой совокупности условий.
Действия над событиями:
Событие С состоит в наступлении хотя бы одного из событий (или).
Событие С состоит в совместном наступлении событий (и).
Событие С означает, что происходит событие А, но не происходит событие В С= ¬А (Противоположное событие) Событие С происходит тогда и только тогда, когда не происходит событие А
|
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами.
Правило суммы: Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами
Правило произведения: Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами
Основные комбинаторные соединения:
(Важен
порядок и состав):
(Важен
состав и повторения):
|
Вероятность события A — отношение количества благоприятных событию A исходов к общему количеству всех равновозможных исходов.
Свойства:
|
|
Прилагательное «дискретная» означает, что вероятности всех событий можно вычислить при помощи суммирования, а не интегрирования.
Из этого вытекают формулы и определения вероятности суммы произвольных событий:
что
Свойства вероятностей:
|
Определение
вероятности по Колмогорову. Отныне
мы будем считать, что нам дано не только
пространство элементарных исходов
P.s. σ – читается как сигма
Определение
1: Функцию
Pr:
Определение
2:
Тройка (
P.s. Соболезную, что попался этот вопрос
|
Условной вероятностью события А при условии, что произошло событие В, называется отношение вероятности одновременного наступления событий А и В к вероятности события В, т.е. величина
Свойства:
|
Два
события А и В называются независимыми
если вероятность их одновременного
наступления равна произведению
вероятностей, т.е. Pr(AB)
= Pr(A)Pr(B),
либо такая запись (
Свойства:
|
События А1, А2,… Аn называются независимыми в совокупности, если
∏ - это, типо, факториал
Есть утверждение «Попарно независимые события не обязательно независимы в совокупности», которое доказывается на контрпримере (пример Бернштейна). Доказательство или же сам пример Бернштейна: покрасим грани тетраэдра в 3 цвета: одну во все 3 цвета (красный, зелёный, жёлтый) и 3 других в различные Рассмотрим следующие события:
Тогда: Приведённые события попарно независимы, но не независимы в совокупности.
|
Последовательность независимых испытаний, в каждом из которых возможно только два исхода (Успех, неудача), с одной и той же вероятностью успеха в каждом испытании, называется схемой Бернулли
Формула Бернулли
Пусть
событие А состоит в том, что в n
испытаниях
Бернулли наступит ровно k
успехов, тогда имеет место быть
равенство:
Наиболее вероятное число успехов.
Обозначим
k0
такое число успехов в n
испытаниях Бернулли, вероятность
которого максимальна, т.е.:
|
Обозначим символом µn число успехов в n испытаниях Бернулли. Вероятность успеха в одном испытании равна 0 < p <1
Введём
следующее обозначение:
Сама теорема Бернулли: Для любого Ɛ > 0 имеет место следующее утверждение:
|
|
Рассматривая последовательность n испытаний Бернулли с вероятностью успеха P в одном испытании и с вероятностью неудачи в одном испытании q = 1-p. Символом Pn(k) обозначим вероятность того, что в n испытаниях наступит ровно k успехов. Введём дополнительное обозначение.
Положим
Имеет
место Локальная
предельная теорема Муавра – Лапласа,
которая предполагает, что k=k(n)
зависит от n
так, что
Тогда
имеет место равенство
Интегральная предельная теорема Муавра – Лапласа: Справедливо следующее соотношение:
При этом сходимость имеет место равномерно по всем a и b в ограниченной области изменения
|
Предположим,
что нам нужна вероятность получить
не менее семи успехов в тысяче испытаний
схемы Бернулли с вероятностью успех
0,003. Высчитать эту вероятность довольно
сложно, поэтому появилась теорема
Пуассона, где
|
Случайной
величиной
Функцией
распределения
называется функция
Пусть
– функция распределения некоторой
случайной величины
|
|
Случайная величина ξ имеет абсолютно непрерывное распределение, если существует неотрицательная функция fξ(x) такая, что для любого х R функция распределения Fξ(x) представима в виде
При этом функция fξ(x) называется плотностью распределения случайной величины ξ.
|
Пусть ξ – случайная величина абсолютно-непрерывного типа с плотностью распределения p(x). Математическим ожиданием случайной величины ξ называется следующая величина
Если
Вместо термина «математическое ожидание» часто используют термины «среднее значение» или «ожидаемое значение» Существуют примеры через:
|
Функция
распределения дискретного типа
является кусочно-постоянной функцией
с разрывами в точках, соответствующим
возможным значениям z1,
z2
,
… случайные величины ξ
и величиной разрыва равной вероятности
pk
в
точке
P.s.
Примеры:
|
Свойство
1: Если
ξ
Это свойство непосредственно следует из определения математического ожидания. Свойство 2: Если P{ξ = a} = 1, то Еξ =a т.е. если случайная величина равна константе с вероятностью равной 1, то её математическое ожидание равно этой же константе. Свойство 3: Линейность. Е(αξ + βη) = αЕξ + βЕη Свойство 4: Монотонность.
|
Дисперсией
случайной величины ξ
называется величина
Свойства:
Пример: Найти дисперсию числа очков при одном подбрасывании кубика. ξ: 1|2|3|4|5|6
p:
M(ξ)=3,5
|
|
Ковариацией случайных величин ξ, η называется следующая величина
Свойства:
|
|
Случайные величины с функциями распределения называются независимыми в совокупности, если функция их совместного распределения удовлетворяет равенству F(x1,…,xn) = F1(x1)*…* Fn(xn) для всех значений x1,…,x
Если случайные величины X и Y независимы, то E(XY) = E(X)E(Y) и, более-того, для широкого класса функций g(x) и h(y) E(g(X) h(Y)) = E(g (X))E(g (Y))
|
|
Моменты старших порядков:
|
|
|
Теорема Хинчина.
Пусть
ξ1,
ξ2,
…, ξn
–
независимые, однако распределённые
случайные величины с конечным
математическим ожиданием, т.е. E|
ξi
|
< ∞,
E
ξi
=
a.
Тогда k
последовательности применим закон
больших чисел, т.е.
|
|
|
|
Теорема Маркова. Если
множество состояний цепи образует
один класс существенных непериодических
состояний, то для всех i.j
= 1,…,N
существует предел
Более
того, для всех j
= 1,…,N
выполнены соотношения
Стационарное распределение.
|
Случайной выборкой объёма n, отвечающей случайной величине X с функцией распределения F(x), называется набор n независимых случайных величин X1, X2,…, Xn каждая из которых имеет распределение F(x)
Генеральная совокупность — это множество всех возможных элементов однородной совокупности. Из этого определения следует, что каждый элемент генеральной совокупности обладает характеристиками генеральной совокупности, но в силу воздействия на него множества случайных факторов эти характеристики в каждом элементе наблюдаются с некоторым отклонением.
|
|
В
качестве оценки для математического
ожидания m
= E(X)
используется оценка
Выборочное среднее является средним значением для эмпирической функции распределения.
|
Выборочная дисперсия – это оценка теоретической дисперсии распределения, рассчитанная на основе данных выборки. Она характеризует среднеквадратичное отклонение выборочных величин от выборочного среднего Выборочные дисперсии бывают: смещёнными и несмещёнными.
Формула
выборочной дисперсии:
|
Точечная
оценка параметра a
определяется ее оценкой
Несмещенной
называется оценка
=
Состоятельной
называется оценка
Эффективной
называется оценка
такая, что
|
Согласно неравенство Р.-К. среднеквадратичное отклонение оценки от оцениваемого параметра не может быть меньше величины, обратной к информационному количеству Фишера. Несмещенная оценка , для которой неравенство Р.-К. обращается в равенство, будет эффективной, т.е. такая оценка имеет мин. дисперсию.
|
Квантиль– значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Вариационный ряд– набор упорядоченных случайных величин. Дискретным вариационным рядом называют упорядоченную совокупность значений случайной величины с соответствующими им частотами или относительными частотами. Интервальным вариационным рядом называют упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений величины.
|
Метод
моментов
заключается в том, что любой момент
случ. величины
Пусть
Суть выборочного метода заключается в том, что для оценки всей совокупности необходимые сведения собираются из определенного числа наблюдений из этой совокупности.
|
Функцией
правдоподобия
для случайных наблюдений
с плотностью распределения
Оценкой
параметра θ, построенной методом
максимального правдоподобия
по наблюдениям
,
называется оценка
|
Имеется
зависимость
Предполагается,
что
Оценки
параметров:
|
Интервал
(
Доверительный
интервал для среднего с известной
дисперсией
имеет вид (
Таким образом, доверительный интервал для среднего с неизвестной дисперсией принимает вид:
|
Статистическая гипотеза — любое предположение о распределении ген. совокупности. Гипотеза наз. простой, если она однозначно определяет распределение ген. совокупности. Иначе она сложная.
Предположим,
что функция распр. случ. величины
нам неизвестна, но мы располагаем
случ. выборкой
По наблюдениям выборки
мы хотим дать ответ на вопрос: совпадает
ли функция распределения
с
некоторой наперед заданной функцией
распределения
Используя наблюдения выборки, нужно либо принять гипотезу о том, что функция распределения совпадает с заданной функцией распределения , либо ее отвергнуть. Правило принятия одного из этих двух решений называется статистическим критерием.
Вероятность
ошибки I рода
— вероятность отвергнуть гипотезу
Вероятность
ошибки II рода
— вероятность принять гипотезу
,
при условии, что верна гипотеза
|
Лемма Неймана-Пирсона– утверждение о том, что в задаче проверки простой статистической гипотезы против простой альтернативы критерий, основанный на отношении правдоподобия, является наиболее мощный. Критерий
Неймана-Пирсона.
Согласно этому критерию, выбирается
такое правило, которое обеспечивает
минимально возможную величину
Проверка
гипотезы о генеральном среднем с
известной дисперсией.
В качестве 0-ой гипотезы возьмем В качестве статистики критерия можно взять функцию
Алгоритм: 1. Выдвигаем нулевую гипотезу и одну из альтернативных; 2. Задаем уровень значимости критерия ; 3.
Вычисляем значение статистики
4.
Находим критическую область,
соответствующую каждой из альтернатив.
В случае, когда
,
рассматривается правосторонняя
критическая область – (
|
Критерий
Пирсона, или критерий
Для проверки вводится статистика: (t–theor, e–emp)
Правило
критерия:
если полученная статистика превосходит
квантиль закона распределения
заданного уровня значимости
с
|
Критерий Колмогорова– непараметрический критерий согласия, в классическом понимании предназначен для проверки простых гипотез о принадлежности анализируемой выборки некоторому известному закону распределения. Наиболее известно применение данного критерия для проверки исследуемых совокупностей на нормальность распределения.
В
основе лежит статистика вида
Интерпретация
значения критерия Колмогорова:
если статистика
|
События. Действия над событиями.
Событие – явление, которое может произойти или не произойти при осуществлении определённой совокупности условий.
Событие является достоверным (Ω), если оно обязательно произойдёт в результате данного опыта.
Событие называется невозможным ( ), если оно заведомо не произойдёт в результате данного опыта.
Два события называются несовместимыми, если появление одного из них исключает появление другого события в одном и том же опыте. В противном случае события называются совместимыми.
Полная группа событий (Ω) – это совокупность единственно возможных событий испытания.
Действия над событиями:
С=А+В (сумма)
Событие С состоит в наступлении хотя бы одного из событий (или).
С=А В (Произведение)
Событие С состоит в совместном наступлении событий (и).
С=А В (Разность)
Событие С означает, что происходит событие А, но не происходит событие В
С= ¬А (Противоположное событие)
Событие С происходит тогда и только тогда, когда не происходит событие А
Классическая вероятность. Свойства вероятностей.
Вероятность события A — отношение количества благоприятных событию A исходов к общему количеству всех равновозможных исходов.
Свойства:
Вероятность достоверного события равна единице
Вероятность невозможного события равна нулю
Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Основные правила комбинаторики. Сочетания, размещения, выбор без возвращения и с возвращением
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами.
Правило суммы: Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами
Правило произведения: Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами
Основные комбинаторные соединения:
Размещение
Размещением из k по n называется n-элементное упорядоченное подмножество k-элементного множества
Размещение без повторения (Важен порядок и состав):
Размещение с повторением (Важен порядок, состав и повторение):
Перестановки
Перестановкой из n элементов называется n-элементное упорядоченное множество
Перестановки без повторений (Важен порядок):
Перестановки с повторениями (Важен порядок и повторение):
Сочетания
Сочетанием из n по k называется k-элементное подмножество n-элементного множества.
Сочетания без повторений (Важен состав):
Сочетания с повторениями (Важен состав и повторения):
Дискретная вероятность и ее свойства.
Прилагательное «дискретная» означает, что вероятности всех событий можно вычислить при помощи суммирования, а не интегрирования.
Из этого вытекают формулы и определения вероятности суммы произвольных событий:
Определение 1: Будем говорить, что на множестве элементарных исходов Ω заданы вероятности элементарных исходов, если на множестве Ω определена неотрицательная функция Pr(ꙍ) такая,
что
Определение 2: Вероятностью события А называется число Pr(A), определённое равенством
Утверждение 1: Для любых событий А и В имеет место равенство:
Утверждение 2: Для любых событий А, В, C имеет место равенство (вероятность суммы трёх событий):
Утверждение 3: Формула включений-исключений
Свойства вероятностей:
Неотрицательность:
Нормированность:
Аддитивность: Если , то

 ),
если оно заведомо не произойдёт в
результате данного опыта.
),
если оно заведомо не произойдёт в
результате данного опыта. В
(Произведение)
В
(Произведение)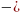 В
(Разность)
В
(Разность)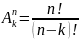
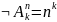




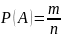


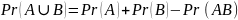



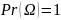
 ,
то
,
то

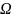 ,
но и выделенная на неё σ-алгебра
подмножеств
,
но и выделенная на неё σ-алгебра
подмножеств
 ℝ,
определённую на событиях из σ-алгебры
,
будем называть вероятностью, если она
удовлетворяет следующим условиям
свойств
вероятности:
ℝ,
определённую на событиях из σ-алгебры
,
будем называть вероятностью, если она
удовлетворяет следующим условиям
свойств
вероятности: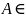

 таких,
что
таких,
что
 справедливо
равенство
справедливо
равенство

 )
называется вероятностным пространством.
)
называется вероятностным пространством.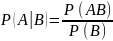



 )
) В,
В,
 ,
,
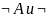 В
В

 Квантор
всеобщности
Квантор
всеобщности



 (k)
(k) ,
где В – произвольное множество
вещественных чисел.
,
где В – произвольное множество
вещественных чисел.

 ,
т.е.
,
т.е.
 .
. ,
где
,
где
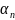 числовая последовательность, сходящаяся
к нулю равномерно по всем
,
числовая последовательность, сходящаяся
к нулю равномерно по всем
,
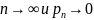 так, что
так, что
 .
Тогда для любого
.
Тогда для любого
 вероятность получить k
успехов в n
испытаний схемы Бернулли с вероятностью
успеха pn
стремится
к величине
вероятность получить k
успехов в n
испытаний схемы Бернулли с вероятностью
успеха pn
стремится
к величине :
:

 называется
функция элементарного исхода такая,
что любого вещественного x
множество
называется
функция элементарного исхода такая,
что любого вещественного x
множество
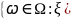

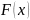 определённая
на всей числовой прямой равенством
определённая
на всей числовой прямой равенством

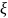 ,
тогда имеют место быть следующие
свойства:
,
тогда имеют место быть следующие
свойства: для любого
для любого
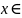 ℝ
ℝ ,
т.е. для любых
,
т.е. для любых имеет место неравенство
имеет место неравенство


 ,
,

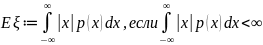 (т.е.
интеграл сходится)
(т.е.
интеграл сходится) ,
то говорят, что математического
ожидания не существует
,
то говорят, что математического
ожидания не существует ,
т.е.
,
т.е.

 -
я без понятия почему в скобке стоит
+, но в учебнике написано так
-
я без понятия почему в скобке стоит
+, но в учебнике написано так
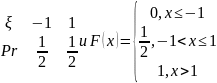
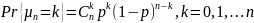
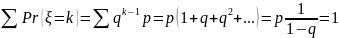
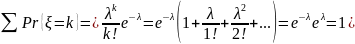
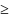 0 с вероятностью 1 и математическое
ожидание существует, то Еξ
0
0 с вероятностью 1 и математическое
ожидание существует, то Еξ
0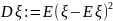
 |
|
|
|
|
|
|
|
|
|
|
|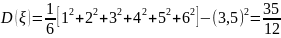

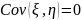

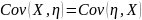



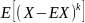
 по вероятности.
по вероятности.
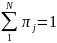 ,
,


 ,
которая называется выборочным средним
,
которая называется выборочным средним
 ,
и ее точность характеризуется дисперсией
оценки.
,
и ее точность характеризуется дисперсией
оценки. такая, что
такая, что
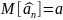 .
.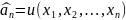 параметра a
такая, что
параметра a
такая, что
 .
. ,
где
,
где
 — любая другая оценка параметра a.
— любая другая оценка параметра a.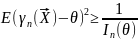 ,
где
,
где
 — оценка параметра
— оценка параметра
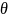 ,
а
,
а
 –
информационное количество Фишера
(количество информации о
,
содержащееся в случайной величине X,
равное
–
информационное количество Фишера
(количество информации о
,
содержащееся в случайной величине X,
равное
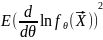 .
.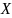 зависит от параметра
.
Но тогда и параметр
может оказаться функцией от теоретического
зависит от параметра
.
Но тогда и параметр
может оказаться функцией от теоретического
 -го
момента. Подставив в эту функцию вместо
неизвестного теоретического
-го
момента его выборочный аналог, получим
вместо параметра 𝜃
оценку
-го
момента. Подставив в эту функцию вместо
неизвестного теоретического
-го
момента его выборочный аналог, получим
вместо параметра 𝜃
оценку
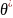 .
. – выборка объема
– выборка объема
 из параметрического семейства
распределений
из параметрического семейства
распределений
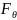 .
Выберем некоторую функцию
.
Выберем некоторую функцию
 так, чтобы существовал момент
так, чтобы существовал момент
 .
Тогда в качестве оценки
для
возьмем решение уравнения
.
Тогда в качестве оценки
для
возьмем решение уравнения
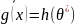 .
. называется функция
называется функция .
. ,
определяемая равенством
,
определяемая равенством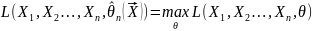 .
.
 являются одинаково распределенными
независ. случ. величинами (iid), независящими
от величин
являются одинаково распределенными
независ. случ. величинами (iid), независящими
от величин
 ,
которые интерпретируются как ошибки
измерения. В свою очередь величины
тоже являются независимыми со средним
ноль (
,
которые интерпретируются как ошибки
измерения. В свою очередь величины
тоже являются независимыми со средним
ноль ( )
и конечной дисперсией (
)
и конечной дисперсией ( ).
По наблюдениям значений пар случайных
величин
).
По наблюдениям значений пар случайных
величин
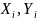 нужно
определить параметры
нужно
определить параметры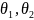 .
Такая модель называется простой
линейной регрессией.
.
Такая модель называется простой
линейной регрессией. ,
,



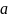 –
некоторое число между [0, 1], а
–
некоторое число между [0, 1], а
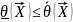 – две случ. функции от выборки
– две случ. функции от выборки
 .
. ,
, )
называется доверительным
интервалом для оценки параметра
,
отвечающим доверительной вероятности
,
если
)
называется доверительным
интервалом для оценки параметра
,
отвечающим доверительной вероятности
,
если
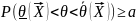 .
. ;
;
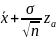 ),
где
),
где
 — это квантиль нормального распределения
уровня
— это квантиль нормального распределения
уровня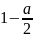 .
. таблицы,
с помощью которых по значениям α и
таблицы,
с помощью которых по значениям α и
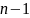 можно определить такое число
можно определить такое число
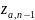 ,
что
,
что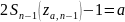 .
. – квантиль порядка
– квантиль порядка
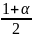 распределения Стьюдента с
степенями свободы, поскольку
распределения Стьюдента с
степенями свободы, поскольку
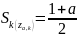 .
.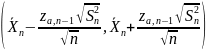
 или
нет. При постановке такой задачи
говорят, что речь идет о проверке
статистической гипотезы.
или
нет. При постановке такой задачи
говорят, что речь идет о проверке
статистической гипотезы.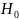 при условии, что она верна.
при условии, что она верна. .
. вероятности
ошибок второго рода при условии, что
вероятность ошибки первого рода не
больше заданной величины
вероятности
ошибок второго рода при условии, что
вероятность ошибки первого рода не
больше заданной величины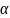 .
. ,
в качестве альтернативной гипотезы
– одну из трех:
,
в качестве альтернативной гипотезы
– одну из трех: ,
,
 или
или
 .
. (1),
где
(1),
где
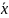 –
выборочное среднее, найденное по
выборке
–
выборочное среднее, найденное по
выборке
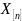 .
.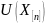 по формуле (1);
по формуле (1); ),
где
),
где
 –
квантиль уровня
–
квантиль уровня
 стандартного
нормального распределения. В случае
же, когда
,
рассматривается левосторонняя
критическая область – интервал (
стандартного
нормального распределения. В случае
же, когда
,
рассматривается левосторонняя
критическая область – интервал ( ),
где
),
где
 –
квантиль уровня α стандартного
нормального распределения.
–
квантиль уровня α стандартного
нормального распределения.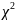 (хи-квадрат)
— применяют для проверки гипотезы о
соответствии эмпирического распределения
предполагаемому теоретическому
распределению
(хи-квадрат)
— применяют для проверки гипотезы о
соответствии эмпирического распределения
предполагаемому теоретическому
распределению
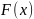 при
большом объеме выборки
при
большом объеме выборки
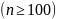 .
Использование критерия
предусматривает разбиение размаха
варьирования выборки на интервалы и
определения числа наблюдений (частоты)
для каждого из интервалов. Для удобства
оценок параметров распределения
интервалы выбирают одинаковой длины.
Число интервалов зависит от объема
выборки.
.
Использование критерия
предусматривает разбиение размаха
варьирования выборки на интервалы и
определения числа наблюдений (частоты)
для каждого из интервалов. Для удобства
оценок параметров распределения
интервалы выбирают одинаковой длины.
Число интервалов зависит от объема
выборки.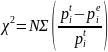 ,
где
,
где
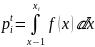 – предполагаемая вероятность попадания
в
– предполагаемая вероятность попадания
в
 ый
интервал,
ый
интервал,
 – соотв. эмпирическое значение;
– соотв. эмпирическое значение;
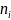 – число элементов выборки из
го
интервала;
– число элементов выборки из
го
интервала;
 – объем выборки.
– объем выборки. или
с
или
с
 степенями
свободы, где
–
число наблюдений или число интервалов,
а
степенями
свободы, где
–
число наблюдений или число интервалов,
а
 –
число оцениваемых параметров закона
распределения, то гипотеза
отвергается;
в противном случае гипотеза принимается
на заданном уровне значимости
.
–
число оцениваемых параметров закона
распределения, то гипотеза
отвергается;
в противном случае гипотеза принимается
на заданном уровне значимости
.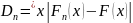 ,
где
,
где
 –
точная верхняя грань множества
–
точная верхняя грань множества
 ,
,
 – функция распределения исследуемой
совокупности,
— функция нормального распределения.
– функция распределения исследуемой
совокупности,
— функция нормального распределения.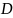 значима (
значима (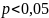 ),
то гипотеза о том, что соответствующее
распределение нормально, должна быть
отвергнута.
),
то гипотеза о том, что соответствующее
распределение нормально, должна быть
отвергнута.