ТВиМС Дополнительное задание

Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра комплексной информационной безопасности электронновычислительных систем (КИБЭВС)

СТАТИСТИЧЕСКИЙ АНАЛИЗ ДАННЫХ

Отчет по индивидуальному заданию по дисциплине «Теория вероятностей и математическая статистика»

Студент гр. 7х3-х

__________ хххххххх

«___» __________ 2025 г.

Руководитель Доцент каф. КИБЭВС, к.т.н.

_______ __________ Ю.В. Шабля

оценка

«___» __________ 2025 г.

Томск 2025

2

Введение

Целью работы является закрепление полученных теоретических знаний в области математической статистики на примере выполнения практических задач с помощью специализированного программного обеспечения.

Задание:

1.Выбрать программное обеспечение для выполнения индивидуального задания;

2.Сформулировать исследуемый процесс, определить целевую функцию и влияющие факторы, сформировать выборку данных;

3.Выполнить проверку статистической гипотезы о виде закона распределения;

4.Провести однофакторный дисперсионный анализ;

5.Провести корреляционный и регрессионный анализ.

Вкачестве исследуемого процесса предлагается рассмотреть работу программы, реализующей сортировку пузырьком для массива убывающих чисел. Целевая функция (выходной параметр) – время сортировки массива. Фактор (входной параметр) – размер массива.

Для выполнения индивидуального задания выбрана программа для работы с электронными таблицами «Microsoft Excel», так как она является мощным инструментом для работы с данными.

3

1 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

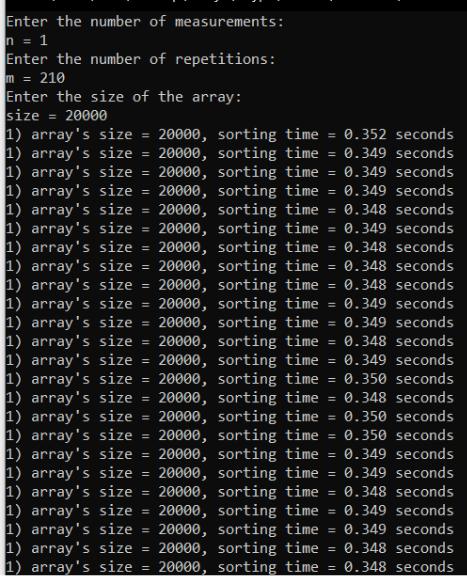
Время сортировки массива принимает разные значения даже при одинаковых значениях входных параметров. Следовательно, можно принять время сортировки массива за некоторую случайную величину, которую обозначим как Y . Далее исследуем вид закона распределения случайной величины Y . Для этого с помощью исследуемой программы сформируем выборку при фиксированном значении входного параметра (размер массива sizе=20 000 элементов) с многократным повторением (m=210 раз). Фрагмент с результатами работы программы представлен на рисунке 1.1.

Рисунок 1.1 – Фрагмент с результатами работы программы

4

Все полученные значения были перенесены в «Microsoft Exсel». Так как случайная величина Y является непрерывной, то в полученной выборке присутствует большое значение различных значений случайной величины с малыми частотами их появления. Такую выборку невозможно исследовать на принадлежность к какому-либо виду закона распределения. Поэтому сгруппируем данные выборки, распределив их на равные интервалы значений, и посчитаем соответствующие частоты попадания в каждый интервал. Количество интервалов определяется по правилу Стёрджеса:

L=1+log2 n ,

где n – объем выборки. Тогда для исследуемой выборки получаем

L=1+log2 210=8.

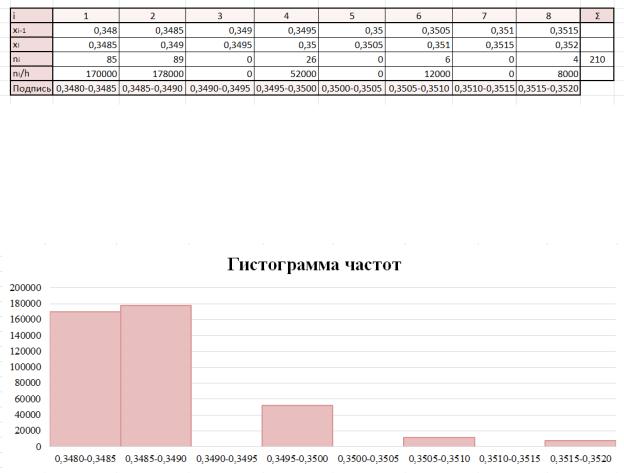
Полученное статистическое распределение выборки в виде интервального ряда представлено на рисунке 1.2.

Рисунок 1.2 – Статистическое распределение выборки

Далее на основе полученного статистического распределения выборки была построена гистограмма частот (рисунок 1.3).

Рисунок 1.3 – Гистограмма частот

5

Исходя из графического представления полученной гистограммы частот, можно сделать следующие выводы о возможном законе распределения случайной величины Y : гистограмма иллюстрирует, что значения распределены неравномерно, распределение ассиметрично. Большая часть данных сосредоточена в левой части гистограммы, а значения в правой части намного меньше по сравнению с началом графика. Это может указывать с большей вероятностью на логнормальное распределение.

Далее проверим статистическую гипотезу о виде закона распределения по критерию Пирсона. В качестве проверяемых законов распределения рассмотрим равномерное и нормальное распределения.

Непрерывная случайная величина X, распределенная по равномерному закону, определяется двумя параметрами (s=2) и имеет следующие функцию плотности распределения вероятностей и функцию распределения вероятностей:

Для получения оценок параметров a и b равномерного распределения воспользуемся методом наибольшего правдоподобия:

{a⃰=min xi=0,348; b⃰=max xi=0,352.

Вычислим теоретические частоты попадания в интервал [xi−1 ; xi ] для равномерного распределения с параметрами a⃰=0,348 и b⃰=0,352 при выборке объема n=210 по формуле:

n'i=n P(X [xi−1 ; xi ])=n (F (xi )−F (xi−1))=n

Вычислим расчетное значение критерия Пирсона по формуле:

K =∑l (ni−n'i )2 =394,7238095 .

набл i=1 ni '

Определим критическое значение критерия Пирсона при уровне значимости α=0 ,05 по формуле:

6

K кр=χ2 (α; l−s−1)=χ2(0,05; 8−2−1)=χ2 (0 ,05; 5)=11,07049769 .

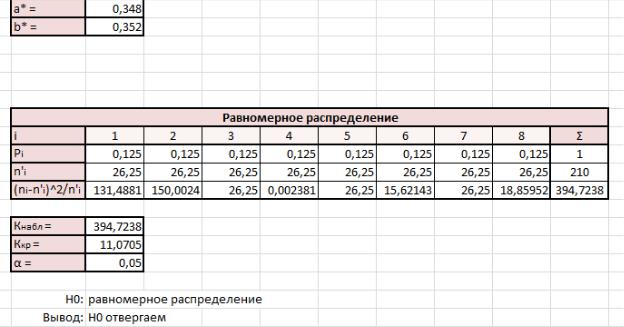
На рисунке 1.4 представлены подробности промежуточных вычислений.

Рисунок 1.4 – Расчеты для равномерного закона распределения

Исходя из проведенных расчетов, можно сделать вывод, что расчетное значение критерия Пирсона больше критического. В таком случае нулевая гипотеза «Равномерное распределение» отвергается.

Непрерывная случайная величина X, распределенная по нормальному закону, определяется двумя параметрами (s=2) и имеет следующие функцию плотности распределения вероятностей и функцию распределения вероятностей:

7

Вычислим теоретические частоты попадания в интервал [xi−1 ; xi ] для нормального распределения с параметрами a =0,3488 и σ =0,0007138 при выборке объема n=210 по формуле:

n'i=n P(X [xi−1 ; xi ])=n (F (xi )−F (xi−1))=

Вычислим расчетное значение критерия Пирсона по формуле:

K набл=∑l (ni−n'i )2 =1233,688474 .

i=1 ni '

Определим критическое значение критерия Пирсона при уровне значимости α=0 ,05 по формуле:

K кр=χ2 (α; l−s−1)=χ2(0,05; 8−2−1)=χ2 (0 ,05; 5)=11,07049769 .

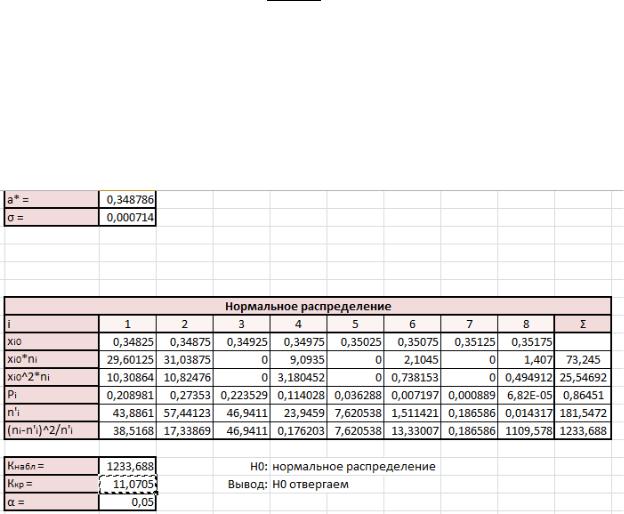
На рисунке 1.5 представлены подробности промежуточных вычислений.

Рисунок 1.5 – Расчеты для нормального закона распределения

Исходя из проведенных расчетов, можно сделать вывод, что расчетное значение критерия Пирсона, также, как и для равномерного распределения, больше критического. В таком случае нулевая гипотеза «Нормальное распределение» отвергается.

8

2 ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

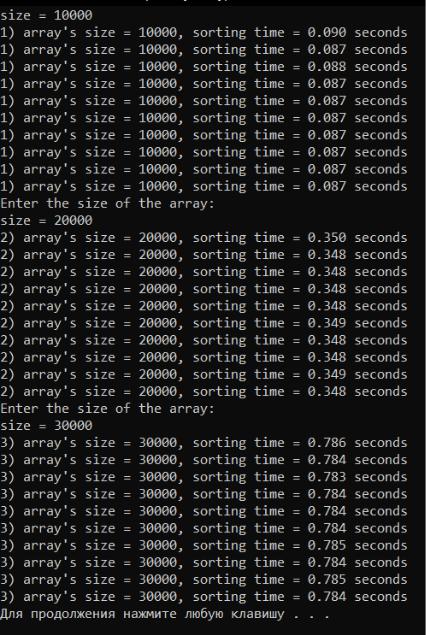
Далее исследуем значимость влияния размера массива убывающих чисел на время его сортировки. Для этого с помощью исследуемой программы сформируем выборку при k =3 фиксированных значениях входного параметра (размер массива siz e1=10 000, siz e2=20 000 и siz e3=30 000 элементов) с многократным повторением (m=10 раз). Фрагмент с результатами работы программы представлен на рисунке 2.1.

Рисунок 2.1 – Фрагмент с результатами работы программы

9

Для выполнения однофакторного дисперсионного анализа необходимо найти несколько статистических характеристик. Во-первых, это средние значения по каждой группе, который вычисляются как сумма всех значений, деленное на их количество. В итоге средняя по первой выборке составила 0,1923, по второй выборке 0,7674, по третьей выборке 1,7255. Среднее значение по всей выборке в целом составила 0,895067. Затем, нужно найти2 фактическое, которое ищется, как сумма коэффициентов по каждой выборке, состоящей из разницы между средним значением по конкретной выборке и среднее значение по выборке в целом, возведенное в квадрат, и умноженное на количество чисел в конкретной выборке. остаточное вычисляется с помощью таблицы, которая изображена на рисунке 2.2, где каждое значение представляет собой значений из первоначальной таблицы, у которого отняли значение среднего по выборке, и после этого возвели в квадрат. 2 фактическое вычисляется как фактическое, делённое на количество выборок минус один. 2 остаточное, как остаточное делённое на разницу между общим количеством значений и количеством выборок.

Далее проверим статистическую гипотезу о значимости влияния фактора по критерию Фишера.

Вычислим расчетное значение критерия Фишера по формуле:

s2

K набл= 2большая =753362,3428. sменьшая

Определим критическое значение критерия Фишера при уровне значимости α=0 ,05 по формуле:

K кр=F (α; k −1 ; k (m−1))=F (0 ,05 ; 3−1 ; 3 (10−1))=

=F (0 ,05; 2 ; 27)=3,354130829 .

На рисунке 2.2 представлены подробности промежуточных вычислений.

10