2 семестр ФИБС / ИКГ / Конспект_по Задачам

18. Построить линии вырезов и срезов.

Построить горизонтальную проекцию сквозного выреза в прямом круговом конусе.

Плоскость, в зависимости от положения в пространстве, может пересекать конус по плоским фигурам ограниченным треугольником, окружностью, эллипсом, параболой, гиперболой или сочетанием данных линий.

В задаче сквозной вырез образован тремя фронтально-проецирующими плоскостями

, и δ.

Основное свойство проецирующих плоскостей заключается в том, что проекцией любой линии, расположенной на этой плоскости, на плоскость проекций, которой она перпендикулярна, является прямая, совпадающая с ее следом.

Последовательность решения задачи:

1. Плоскость является горизонтальной, перпендикулярной оси конуса. Она пересекает конус по плоской фигуре, ограниченной дугами окружности (1–3, 2–4).

Эти дуги проецируются на π1 в натуральную величину. Горизонтальные проекции точек 1/, 2/, 3/, 4/ строим исходя из принадлежности их поверхности конуса.

2. Плоскости и δ не параллельны ни одной образующей конуса,

следовательно, они пересекают конус по плоской фигуре ограниченной дугами эллипсов 1–5–9, 3–7–9, 2–6–10, 4–8–10. Фронтальные проекции (5//, 6//, 7//, 8//, 9//, 10//)

точек отмечаем на фронтальных проекциях плоскостей. Горизонтальные проекции строим исходя из принадлежности их поверхности конуса.

3. Обводим видимый контур проекций конуса со сквозным вырезом сплошной основной линией. Строим линии пересечения плоскостей , и δ (1–2, 3–4, 9 – 10), учитываем их видимость.

Построить горизонтальную проекцию сквозного выреза на шаре.

Любая плоскость рассекает шар по кругу. Если секущая плоскость параллельна плоскости проекций, то круг проецируется на эту плоскость в натуральную величину, если нет – то в эллипс. Задан шар с вырезом образованным двумя фронтально-проецирующими плоскостями и . Построить вырезы на горизонтальной и фронтальной проекциях.

Последовательность решения задачи:

1.Плоскость является горизонтальной. Она пересекает шар по плоской

фигуре, ограниченной дугой окружности (2–1–3). Эта дуга проецируются на π1 в натуральную величину. Горизонтальные проекции точек 1/, 2/, 3/ строим исходя из принадлежности их поверхности шара.

2.Плоскость не параллельна π1, следовательно, горизонтальная проекция сечения - плоская фигура ограниченная дугой эллипса. Отмечаем на фронтальной проекции выреза следующие точки: 4 – точка малой оси эллипса сечения; 5,6 – большая ось эллипса сечения; 7,8 – характерные точки сечения, лежащие на экваторе сферы; 9,10 – дополнительные точки, характерные для профильной проекции. Горизонтальные проекции точек строим исходя из принадлежности их поверхности шара, применяя вспомогательные плоскости α i.

3.Обводим видимый контур проекций шара со сквозным вырезом сплошной

основной линией. Строим линию пересечения плоскостей и (2/ – 3/), учитываем видимость.

Построить проекции сквозных вырезов в теле на трёх плоскостях проекций

19.Построить линию пересечения поверхностей

Взависимости от вида и взаимного положения поверхностей линия их пересечения может быть прямой, плоской или пространственной ломаной, плоской или пространственной кривой.

Линия пересечения двух поверхностей одновременно принадлежит обеим поверхностям. Построение линии пересечения сводится к нахождению ряда её точек, принадлежащих одновременно обеим поверхностям. Точки линии пересечения условно делятся на характерные (опорные) и промежуточные. Характерными являются экстремальные точки, очерковые точки, точки смены видимости. Характерные точки обязательно строят на эпюре. Промежуточные точки определяют для более точного построения линии пересечения.

Точки, принадлежащие линии пересечения определяются (в основном) методом вспомогательных секущих поверхностей. В качестве вспомогательных поверхностей наиболее часто используются плоскости и сферы. В некоторых задачах бывает целесообразно применять цилиндрические и конические поверхности. Если одна из пересекающихся поверхностей занимает проецирующее

положение, то решение задачи может быть сведено к построению недостающих проекции линии, принадлежащей поверхности.

Простота и точность решения задачи зависит от правильности выбора вспомогательных секущих поверхностей. Любая вспомогательная секущая поверхность должна пересекать каждую из заданных поверхностей по линиям, проекции которых являются графически простыми линиями – прямыми или окружностями.

Точки, принадлежащие линии пересечения поверхностей (κ, ψ) находятся по следующему алгоритму:

1.Вводится вспомогательная секущая поверхность (плоскость) α1, пересекающая заданные поверхности κ и ψ по графически простыми линиями.

2.Определяются линии пересечения вспомогательной поверхности (плоскости) с каждой из заданных поверхностей.

3.Отмечаются точки пересечения построенных линий пересечения. Эти точки одновременно принадлежит заданным поверхностям κ и ψ, следовательно, принадлежат линии их пересечения.

4.Пункты 1, 2, 3 повторяются необходимое количество раз для определения всех опорных и достаточного количества промежуточных точек линии пересечения.

5.Через построенные точки проводится линия пересечения поверхностей.

6.Определяется видимость поверхностей и линии пересечения.

Построим на горизонтальной и фронтальной проекциях линию пересечения поверхности конуса и полусферы.

Задача может быть решена методом вспомогательных секущих плоскостей.

Определим характерные точки линии пересечения.

1.Проводим вспомогательную фронтальную секущую плоскость α1 (заданную горизонтальным следом h0α1) проходящую через вершину конуса.

2.Плоскость α1 пересекает конус по образующим AS и BS. ASB = α1 ∩ κ. Плоскость α1 пересекает полусферу по меридиану CD. CD = α1 ∩ ψ.

3.Отмечаем точку пересечения построенных линий пересечения.

1 = ASB ∩ CD. (1// = ASB// ∩ CD//, 1/ h0α1). Точка 1 является наивысшей точкой сечения.

4.Вторую вспомогательную фронтальную секущую плоскость проведём по горизонтальной плоскости проекций α2 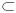π1.

5.Плоскость α2 пересекает конус по основанию. Плоскость α2 пересекает полусферу по экватору.

6.Отмечаем точки пересечения построенных линий пересечения 2/ и 3/, 2// f0α1 и 3// f0α1 . Точки 2 и 3 являются низшими точками сечения.

Определим промежуточные точки линии пересечения.

7.Проводим вспомогательную горизонтальную секущую плоскость α3 (заданную фронтальным следом f0α3).

8.Плоскость α3 пересекает конус по окружности r3κ. Измеряем величину радиуса на фронтальной проекции и строим горизонтальную проекцию линии пересечения.

Плоскость α3 пересекает полусферу по окружности r3ψ. Измеряем величину радиуса на фронтальной проекции и строим горизонтальную проекцию линии пересечения.

9.Отмечаем точки пересечения построенных линий пересечения 4/, 5/ = r/3κ ∩ r/3ψ; 4//, 5// f0α3.

10.Проводим вспомогательную горизонтальные секущие плоскостьи α4 и α5,

повторяем построения и находим промежуточные точки 6, 7, 8, 9.

11.Через построенные точки проводим линию пересечения поверхности конуса и полусферы.

12.Определяем и показываем на эпюре видимость поверхностей и линии пересечения.

20.Построить развёртку поверхностей пирамиды, призмы методом нормального сечения, призмы методом раскатки, конуса, цилиндра.

Многогранники

Разверткой поверхности многогранника, в том числе пирамиды, называется плоская фигура, состоящая из граней данной поверхности, полученная последовательным совмещением всех граней с плоскостью чертежа.

Существуют три основных способа построения развёрток многогранников (способ нормального сечения, способ раскатки, способ треугольников). Первые два из них применяются для построения развёрток поверхностей призм. Развертка поверхности пирамиды строится при помощи способа треугольников.

Развертка поверхности пирамиды представляет собой плоскую фигуру, состоящую из боковых граней пирамиды – треугольников и многоугольника

основания. Построение развертки пирамиды сводится к определению натуральной величины основания и боковых граней пирамиды.

Рассмотрим построение развертки поверхности наклонной треугольной пирамиды.

Последовательность построения развертки: - определяем натуральную величину основания пирамиды.

Данная пирамида стоит своим основанием на горизонтальной плоскости проекций

π1, следовательно натуральная величина основания призмы уже известна

|ABC|=A/B/С/ ;

-определяем истинную (натуральную) величину боковых рёбер пирамиды.

Используем метод вращения. Через вершину пирамиды проводится ось вращения i ┴ π1; S 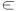i. Ребра пирамиды вращением переводятся в частное положение фронтальных прямых.

-строим развёртку поверхности пирамиды.

Проводим произвольную прямую а, отмечаем на ней точку S0 и при помощи циркуля (метод засечек) откладываем отрезок S0B0=|S1//B1//|. Строим боковую грань SBС, для этого из точки B0 проводим циркулем засечку радиусом |B/C/| (натуральная величина отрезка BC), а из точки S0 вторую засечку радиусом |S1//С1//| (натуральная величина отрезка BC). Пересечение засечек определяет положение точки С0. Аналогично методом засечек строятся все остальные точки, соединив их и показав линии изгиба получаем развёртку поверхности пирамиды

перпендикуляры, на которых соответственно отложить длины ребер от нормального сечения до вершин призмы.

Соединив полученные точки ломаными линиями, получим развертку боковой поверхности призмы.

Поверхности вращения

Развертки поверхностей вращения строится алгебраическим или графическим способом. Алгебраический способ – часть элементов развертки строится с использованием математических формул. Графический способ – развертка строится только графически.

Для того, чтобы построить развертку, например, боковой поверхности наклонного кругового конуса графическим способом, необходимо вписать в него наклонную пирамиду основание у которой правильный многоугольник, а ребра равны образующим поверхности. При этом чем больше углов (следовательно и ребер) у пирамиды, тем точнее развертка. В этом случае развертка конуса заменяется разверткой n-угольной пирамиды. Рассмотренная развертка боковой поверхности наклонного кругового конуса является приближенной.

Построим алгебраическую развертку поверхности прямого кругового конуса. Развертка прямого кругового конуса представляет собой сектор, радиус которой равен длине образующей l=L, а угол сектора вычисляется по формуле α° = 360°R/L и окружность радиуса R, ограничивающая поверхность основания.

Построим алгебраическую развертку поверхности прямого кругового цилиндра.

Развертка поверхности прямого кругового цилиндра представляет собой прямоугольник, у которого одна сторона равна его образующей Н, а другая сторона вычисляется по формуле L = 2πR (мм) и двух окружностей радиуса R, ограничивающих поверхности оснований.