
2 семестр ФИБС / ИКГ / Конспект_по Задачам
.pdf
ЗАДАЧИ.
«Начертательная геометрия. Инженерная графика»
1. Точка в различных пространственных углах

2. Определить натуральную величину отрезка и углы наклона к пл. проекций различными способами
Натуральную величину отрезка и углы его наклона к плоскостям проекций можно определить, используя метод треугольника (метод Монжа), или применяя методы преобразования ортогональных проекций (замена плоскостей проекций, вращение, плоскопараллельное перемещение и др.).
Способ треугольников
Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым – разность координат концов отрезка, взятая с соответствующей проекции.
Угол наклона отрезка (прямой) к плоскости (в том числе и к плоскостям проекций) равен углу между этой прямой и ее проекцией на плоскость.
На горизонтальной проекции построим прямоугольный треугольник один катет которого горизонтальная проекция отрезка (А/В/), а второй разность координатz концов отрезка ( z = Аz - Вz). Гипотенуза треугольника равна натуральной величине отрезка (LАВ = А/В0). Угол α0, лежащий напротив катета z равен углу наклона отрезка к горизонтальной плоскости проекций.
Аналогично решим задачу на фронтальной и профильной проекции. Выполним проверку точности построений: А/В0 = А0В// = А///В0.

Замена плоскостей проекций
Отрезок проецируется на плоскость проекций в натуральную величину, если он параллелен этой плоскости проекций. Для решения задачи надлежит ввести новую плоскость проекций расположенную в пространстве перпендикулярно одной из исходных плоскостей проекций и параллельно заданному отрезку.

Последовательность решения задачи:
1. Найдём натуральную величину отрезка АВ и угол наклона к плоскости проекций π1.
Используем горизонтальную (π1) и фронтальную (π2) плоскости проекции. Переходим к новой системе плоскостей проекций. Горизонтальную плоскость проекций оставляем на месте. Фронтальную плоскость проекций меняем на новую, расположенную параллельно отрезку АВ.
x |
|
2 |
x |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
; |
|
// x // |
|
/ |
|
|
|
|
||
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
4 |
1 |
|
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отрезок проецируется на плоскость π4 |
в натуральную величину LАВ = АІVВІV, а |
||||||||||||||||||||
угол α0 между проекцией отрезка на плоскость π4 |
и осью x1 равен углу наклона |
||||||||||||||||||||
отрезка к плоскости проекций π1. |
( |
IV |
|
IV |
, x ) ( , ) |
. |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично решим задачу используя другие пары плоскостей проекций.
2. Найдём натуральную величину отрезка АВ и угол наклона к плоскости проекций π2.
Используем горизонтальную (π1) и фронтальную (π2) плоскости проекции. Переходим к новой системе плоскостей проекций. Фронтальную плоскость проекций оставляем на месте. Горизонтальную плоскость проекций меняем на новую, расположенную параллельно отрезку АВ.
x |
|
2 |
x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
// x |
|
// |
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
// |
|
// |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
5 |
|
5 |
|
2 |
|
5 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отрезок проецируется на плоскость π5 |
в натуральную величину LАВ = АVВV, а |
|||||||||||||||||||||||||
угол 0 |
между проекцией отрезка на плоскость π5 |
и осью x2 равен углу наклона |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
, x |
|
) ( , |
|
). |
||||
отрезка к плоскости проекций π2. |
|
|
|
V |
|
V |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
|
Найдём натуральную величину отрезка АВ и угол наклона к плоскости |
||||||||||||||||||||||||
проекций π3.
Используем фронтальную (π2) и профильную (π3) плоскости проекции. Переходим к новой системе плоскостей проекций. Профильную плоскость проекций оставляем на месте. Фронтальную плоскость проекций меняем на новую, расположенную параллельно отрезку АВ.
z |
|
3 |
z |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
// z |
|
// |
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
/// |
/// |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
6 |
|
6 |
|
3 |
|
6 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отрезок спроецируется на плоскость π6 в натуральную величину LАВ = АVІВVІ, а угол 0 между проекцией отрезка на плоскость π6 и осью z1 равен углу наклона отрезка к плоскости проекций π3. ( VI VI , z1 ) ( , 3 ).
4. Выполним проверку точности построений: IV IV V V VI VI .

Плоскопараллельное перемещение
Вращение вокруг осей, перпендикулярных плоскостям проекций.
Для решения задачи надлежит повернуть отрезок до положения параллельного одной из плоскостей проекций.
Целесообразно проводить ось вращения через один из концов отрезка. Проведём ось i перпендикулярно горизонтальной плоскости проекций и
проходящую через точку В.
Повернём отрезок АВ вокруг оси до положения параллельного фронтальной плоскости проекций. Точка В своего положения в пространстве не изменит, т.к. она принадлежит оси вращения. Горизонтальная проекция точки А переместится по
дуге окружности, а фронтальная по прямой параллельной оси x.
Отрезок проецируется на плоскость π2 |
в натуральную величину |
|
// |
|
1 |
||||
|
||||
|
|
|
Угол α0 между проекцией отрезка на плоскость π2 и осью x равен углу отрезка к плоскости проекций π1.
|
// |
L |
|
. |
|
|
|||
1 |
|
|
|
|
|
|
|
наклона

Вращение вокруг осей, параллельных плоскостям проекций
Совмещение

3. Определение следов и натуральной величины отрезка
Определение натуральной величины отрезка рассмотрено выше.
Следом прямой называется точка ее пересечения с плоскостью проекций
(Н,F,P).
В системе двух плоскостей проекций (π1 π2 ) прямая в общем случае имеет два следа: горизонтальный Н и фронтальный F — точки пересечения прямой с горизонтальной и фронтальной плоскостями проекций.
Горизонтальный след: H = АВ ∩ π1. (z = 0). Фронтальный след: F = АВ ∩ π2. (у = 0).
AB : ∞, IV, H ( пп π1 ), I, F ( вп π2 ), II, ∞
Видимость-наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций.
4. Определение точки пересечения прямой с плоскостью
Порядок решения задачи
1.Заключаем прямую АВ во вспомогательную секущую плоскость β.
2.Строим линию пересечения вспомогательной плоскости с заданной плоскостью DEF – 12.
3.Находим точку пересечения прямой АВ с заданной плоскостью - К.
4.Определяем видимость прямой.

5. Построение прямой перпендикулярной к плоскости
Прямая перпендикулярна плоскости , если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости
Чтобы эти прямые углы спроецировались в натуральную величину (см. теорему о проецировании прямого угла), прямые должны быть параллельны плоскостям проекций, т. е. являться горизонталью и фронталью плоскости.
Следовательно, прямая a перпендикулярна плоскости, если она перпендикулярна пересекающимся горизонтали h и фронтали f этой плоскости.
6. Найти расстояние от точки до прямой
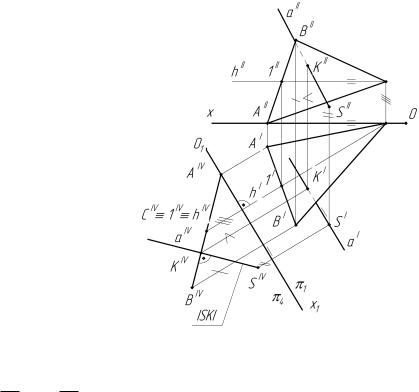
Заданы прямая АВ и точка S. Определить расстояние от этой точки до прямой. Решаем задачу методом двойной замены плоскостей проекций, как показано
на чертеже.

7. Найти расстояние между параллельными прямыми
Расстояние между двумя параллельными прямыми измеряется длиной отрезка перпендикуляра, опущенного из произвольной точки одной прямой на другую прямую.
8. Найти расстояние между скрещивающимися прямыми
Расстояние между двумя скрещивающимися прямыми измеряется длиной отрезка, перпендикулярного этим прямым. Если одна из прямых перпендикулярна плоскости проекций, то перпендикуляр к ней будет параллелен этой плоскости проекций и спроецируется без искажения. Кроме того, прямой угол между перпендикуляром и прямой, на плоскость проекций также спроецируется без искажения (теорема о проецировании прямого угла). В том случае, когда обе скрещивающиеся прямые произвольно расположены относительно плоскостей проекций, необходимо одним из известных способов (плоскопараллельным перемещением или заменой плоскостей проекций) преобразовать чертеж так, чтобы одна из заданных прямых стала проецирующей.
Решим задачу способом замены плоскостей проекций.
9. Найти расстояние от точки до плоскости
Кратчайшее расстояние от точки до плоскости определяется длиной отрезка перпендикуляра опущенного из точки на плоскость. Решение задачи в обще случае включает в себя последовательное выполнение следующих операций: строим через точку перпендикуляр к плоскости; находим точку пересечения перпендикуляра с плоскостью; определяем натуральную величину длины отрезка перпендикуляра.
Задача может быть решена несколькими способами. Для решения можно не использовать методы преобразования ортогонального чертежа (метод Монжа), или применить один из них (замена плоскостей проекций, вращение, плоскопараллельное перемещение). В большинстве случаев, если плоскость находится в общем положении, целесообразно применять метод замены плоскостей проекций.
Заданы проекции плоскости АВС и точка S. Определим кратчайшее расстояние между ними.
1. |
|
Заменим фронтальную плоскость проекций (π2) на новую (π4), |
||||||||||||||||
расположенную перпендикулярно треугольнику АВС. |
|
|
|
|
|
|
|
|||||||||||
x |
|
2 |
x |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
4 1 ; 4 |
С x1 h |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
; |
|
/ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|||
Построим проекцию треугольника и точки на (π4). |
IV |
IV |
IV |
- отрезок прямой. |
||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||
2. Через точку А строим прямую а перпендикулярно плоскости
a
3.
С a IV IV IV C IV a/ / / C / a/ h/ .
Находим точку К пересечения перпендикуляра с плоскостью.
K IV AIV IV C IV a IV ; K / a/
Фронтальную проекцию К// находим, как показано на рисунке, или через построение фронтали плоскости.
3. Определяем натуральную величину кратчайшего расстояния.
ABC 4 , a ABC a IV // 4 S IV K IV LSK
5.Определяем, применяя метод конкурирующих точек, и показываем на эпюре видимость прямой а.
