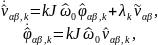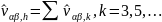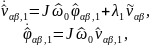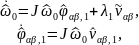4. Синтез системы при несимметрии сети

В качестве источника трехфазного сигнала используются три гармонических источника амплитудой 100 В со сдвигом фаз 2π/3 рад (120°) и с частотой 100π рад/с (ϖ₀ = 100π). Структурная схема источника трехфазного сигнала с учетом появления несимметрии в сети представлена на рисунке Рисунок 2 .1. Полная структурная схема системы ФАПЧ в фиксированной системе координат представлена в приложении А.

Рисунок 2.4 — Структурная схема системы при наличии несимметрии

Моделирование проводится при изменении амплитуды одной из фаз на 20 В (наличие обратной последовательности с амплитудой 20 В) системы abc в момент времени 1,0 с. Результаты моделирования представлены на рисунке Рисунок 2 .1. Листинг программы приведен в приложении В.

Рисунок 2.5 — Результаты моделирования ФАПЧ при несимметрии сети

5. Синтез системы при несинусоидальности сети

Моделирования проводится при возникновении третей и пятой гармоник, характеризуемых амплитудой 10 В и 5 В соответственно. Структурная схема источника трехфазного сигнала с учетом появления несимметрии и несинусоидальности в сети представлена на рисунке Рисунок 2 .1. Результаты моделирования представлены на рисунке Рисунок 2 .1.

Рисунок 2.6 — Структурная схема системы при наличии несинусоидальности

Рисунок 2.7 — Результаты моделирования ФАПЧ при несинусоидальности сети

3. Синтез расширенной фапч при несинусоидальности сети

С целью учета появления в сети гармоник, рассмотренная в главе 2, система ФАПЧ может быть улучшена. Для этого в [3] предлагается ввести в схему контур компенсации гармоник, при этом их порядок не ограничен. Данный контур учитывает работу системы в условиях несимметричных и несинусоидальных искажений. Предыдущая система ФАПЧ, описанная в главе 2, не включает явного метода для подавления гармонических искажений, поэтому результирующая оценка частоты в ней характеризуется небольшой пульсацией (см. рисунок 2.7).

Приведенная ниже расширенная система ФАПЧ включает в себя контур для оценки квадратурных сигналов, состоящий из блока для компенсации гармоник, контур для оценки исходной частоты и контур для оценки прямой и обратной последовательностей.

1. Контур для компенсации гармонических искажений

Метод, лежащий в основе данного контура, заключается в составлении системы, который бы оценивал гармонически искаженную часть напряжения сети 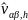. С учетом уравнений ( 1 .8) математическая модель для оценки гармоники k-го порядка описывается уравнениями

(3.16)

где 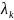– коэффициент усиления для каждого контура гармоники k-го порядка.

Результирующее значение искаженной части сети определяется по формуле

(3.17)

Структурная схема такого контура представлена на рисунке 3.1.

Рисунок 3.8 — Контур для оценки результирующих гармонических искажений (на схеме представлен как v_alpbetH_est)

2. Оценка выходных сигналов

В таком случае регулирование исходного сигнала происходит также с учетом сигнала . Из уравнений ( 3 .16) для сигналов основной частоты справедливо

(3.18)

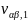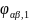Структурная схема для оценки сигналов основной частоты и представлена на рисунке 3.2. Отличие со схемой на рисунке 2.1 заключается во введении в обратную связь контура оценки гармонических искажений.

Оценка частоты определяется уравнением

(3.19)

Структурная схема для оценки частоты представлена на рисунке 3.3.

Аналогично главе 2, уравнения для симметричных составляющих основной частоты выражаются в виде

(3.20)

Рисунок 3.9 — Структурная схема для оценки сигналов и 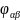основной частоты (на схеме представлены как v_alpbet1_est и phi_alpbet1_est соответственно)

Рисунок 3.10 — Структурная схема для оценки частоты (на схеме сигнал представлен как w_0_ est)

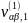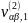Рисунок 3.11 — Структурная схема для оценки симметричных составляющих и (на схеме сигналы представлены как v1_alpbet1 и v2_alpbet1)