ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Б.К.Акопян
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №6

ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

по курсу: ПРИКЛАДНЫЕ МЕТОДЫ ОТПТИМИЗАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: освоить и закрепить практические навыки по принятию и обоснованию решений в условиях недостатка информации, когда один из игроков не имеет конкретной цели и случайным образом выбирает очередные «ходы».

Вариант 20:

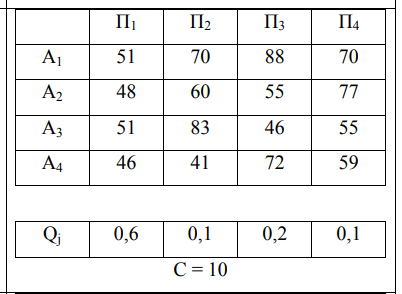
Рисунок 1- Платежная матрица, вероятности и затраты на эксперимент

Ход работы:

Для оптимизации матрицы удалены невыгодные стратегии игрока А (Рисунок 1).

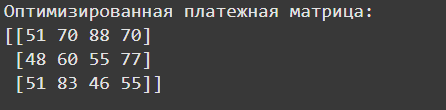
Рисунок 1 – Вывод условий задания

Посчитана матрица рисков, которая показывает, насколько каждая стратегия уступает оптимальной стратегии в каждом состоянии (Рисунок 2).

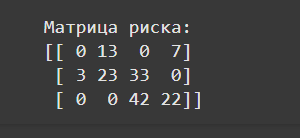
Рисунок 2- Матрица риска

Первая стратегия наиболее стабильна, и она дважды является оптимальной.

Для выбора оптимальной стратегии применен критерий Вальда. Для каждой стратегии берётся минимальный возможный выигрыш, затем выбирается стратегия с наибольшим из минимальных значений (Рисунок 3).

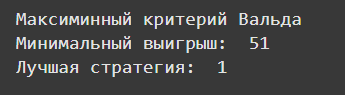
Рисунок 3- Применение критерия Вальда

Применение критерия Вальда показало, что стратегия 1 является наилучшим выбором в условиях неопределенности.

Рассчитан критерий Сэвиджа, который минимизирует возможные потери (Рисунок 4).

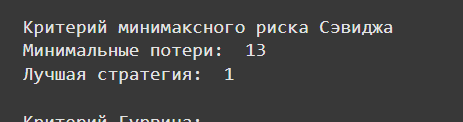
Рисунок 4- Критерий Сэвиджа

Стратегия с минимальным максимальным риском – стратегия 1, так как она минимизирует наибольшие потери, которые могут возникнуть в случае наихудшего исхода.

Рассчитан критерий Гурвица, который сочетает оптимизм (ориентация на максимальный результат) и пессимизм (учет минимального результата) через коэффициент пессимизма.

Рисунок 5- Критерий Гурвица

Для всех значений коэффициента стратегия 1 является оптимальной.

Затем рассчитан критерий Лапласа, который предполагает, что все возможные исходы для каждой стратегии равновероятны. Вычисляются средние значения для каждой стратегии, которые показывают её средний результат (Рисунок 6).

Рисунок 6- Критерий Лапласа

Самое наибольшее среднее значение для стратегии 1.

Рассчитан средний выигрыш и средний риск для каждой стратегии (рисунок 7).

Рисунок 7- Средний выигрыш и средний риск

Средний выигрыш показывает, что стратегия 1 приносит наибольшую выгоду если принять во внимание вероятности всех возможных состояний природы.

Средний риск для стратегии 1 минимален, что делает её оптимальной. Так как средний риск меньше стоимости эксперимента, значит эксперимент связан с излишними затратами, которые не оправданы улучшением результата. Рекомендуется применить стратегию А1.

Вывод: в ходе выполнения лабораторной работы были освоены практические навыки по принятию и обоснованию решений в условиях недостатка информации, когда один из игроков не имеет конкретной цели и случайным образом выбирает очередные «ходы». Разработана программа для нахождения оптимальной стратегии с помощью различных критериев. Все критерии указали оптимальной стратегию А1.

ПРИЛОЖЕНИЕ А

import numpy as np

import pandas as pd

payment_matrix = np.array([

[51, 70, 88, 70],

[48, 60, 55, 77],

[51, 83, 46, 55],

])

probabilities = np.array([0.6, 0.1, 0.2, 0.1])

C = 10

print("Оптимизированная платежная матрица:")

print(payment_matrix)

max_in_columns = np.max(payment_matrix, axis=0)

risk_matrix = max_in_columns - payment_matrix

print("\nМатрица риска:")

print(risk_matrix)

min_values = np.min(payment_matrix, axis=1)

W = np.max(min_values)

strategy = np.argmax(min_values) + 1

print("\nМаксиминный критерий Вальда" )

print("Минимальный выигрыш: ", W )

print("Лучшая стратегия: ", strategy )

max_risks = np.max(risk_matrix, axis=1)

W = np.min(max_risks)

strategy = np.argmin(max_risks) + 1

print("\nКритерий минимаксного риска Сэвиджа" )

print("Минимальные потери: ", W )

print("Лучшая стратегия: ", strategy )

gamma_values = [0, 0.2, 0.5, 0.8, 1]

for gamma in gamma_values:

min_values = np.min(payment_matrix, axis=1)

max_values = np.max(payment_matrix, axis=1)

hurwicz_values = gamma * min_values + (1 - gamma) * max_values

W = np.max(hurwicz_values)

strategy = np.argmax(hurwicz_values) + 1

hurwicz_results[gamma] = (W, strategy)

print("\nКритерий Гурвица:")

for alpha, (value, strategy) in hurwicz_results.items():

print(f" γ = {alpha:.1f}: Лучшая стратегия {strategy}, значение {value:.2f}")

averages = np.mean(payment_matrix, axis=1)

W = np.max(averages)

strategy = np.argmax(averages) + 1

print("\nКритерий Лапласа" )

print("Среднее значение: ", W )

print("Лучшая стратегия: ", strategy )

average = np.dot(payment_matrix, probabilities)

a = np.max(average)

best_strategy = np.argmax(average) + 1

print(f"\nСредний выигрыш без эксперимента: {a:.2f}")

print(f"Лучшая стратегия без эксперимента: {best_strategy}")

average_risks = np.dot(risk_matrix , probabilities)

min_risk = np.min(average_risks)

min_risk_strategy = np.argmin(average_risks) + 1

print(f"\nСредние риски по стратегиям: {average_risks}")

print(f"Минимальный средний риск: {min_risk:.2f}")

print(f"Стратегия с минимальным риском: {min_risk_strategy}")

if C < min_risk:

print("\nЭксперимент целесообразно проводить.")

else:

print("\nЭксперимент проводить нецелесообразно.")