ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Б.К.Акопян
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

РЕШЕНИЕ ОДНОМЕРНОЙ ЗАДАЧИ ОПТИМИЗАЦИИ

по курсу: ПРИКЛАДНЫЕ МЕТОДЫ ОТПТИМИЗАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: изучение алгоритмов поиска экстремума унимодальной функции, определение сравнительной эффективности методов одномерной оптимизации.

Вариант 10:

Рисунок 1- Функция, интервал и погрешность определения экстремума

Ход работы:

Аналитическим методом вычислен экстремум функции на заданном интервале.

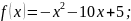
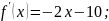
Нахождение критических точек

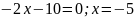
Критическая точка x=-5 попадает в заданный интервал [-6,6;-4]

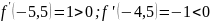, так, как до точки -5 функция возрастает, после точки x=-5 функция убывает. Значит точка x =-5 - точка максимума.

Реализован алгоритм равномерного поиска экстремума, который основан на построении сетки узлов на интервале и последовательном его сокращении, пока длина интервала не станет меньше заданной точности (Листинг 1).

Листинг 1- Алгоритм равномерного поиска экстремума

import numpy as np

def f(x):

return -x**2 - 10*x + 5

def search_algoritm(a, b, N, e):

# Начальный интервал

interval_length = b - a

iteration = 0

while interval_length > e:

iteration += 1

# Разбитие интервала на N+1 узел

x_values = np.linspace(a, b, N+1)

#Вычисление функции в узлах

f_values = f(x_values)

# максимальное значение функции и индекс этой точки

max_index = np.argmax(f_values)

x_max = x_values[max_index]

f_max = f_values[max_index]

# Сужение интервала

if max_index == 0:

# Максимум в левой границе

b = x_values[1]

elif max_index == N:

# Максимум в правой границе

a = x_values[N-1]

else:

# Максимум внутри

a = x_values[max_index - 1]

b = x_values[max_index + 1]

interval_length = b - a

return x_max, iteration, a, b

a = -6.6

b = -4

N = 30 # Количество узлов сетки (чем больше узлов, тем меньше итераций)

e = 2**(-17)

x_max, iterations, final_a, final_b = search_algoritm(a, b, N, e)

print(f"Максимум функции достигается в точке x = ",x_max)

print(f"Количество итераций: ", iterations)

print(f"Итерации завершились на интервале [{final_a}, {final_b}]")

Рисунок 2- Максимум функции, число итераций и конечный интервал

Найденный с помощью алгоритма экстремум функции совпал с экстремумом, полученным ручным способом. Алгоритму потребовалось 5 итераций для нахождения экстремума при количестве узлов n=30.

Затем реализован алгоритм дихотомии, который основывается на последовательном делении интервала пополам. Вычисляются значения функции в точках и в зависимости от того, какое значение функции больше, интервал сужается. Если правое значение больше левого, то максимум находится в правой части, и изменяется левая граница интервала (Листинг 2).

Листинг 2- Реализация алгоритма дихотомии

def f(x):

return -x**2 - 10*x + 5

def search_with_dichotomy(a, b, e, G):

iteration = 0

interval_length = b - a

while interval_length > e:

iteration += 1

# срединная точка интервала

x = (a + b) / 2

# точки для проверки

x1 = x - G

x2 = x + G

f_x1 = f(x1)

f_x2 = f(x2)

if f_x1 < f_x2:

a = x

else:

b = x

interval_length = b - a

return (a + b) / 2, iteration, a, b

a = -6.6

b = -4

e = 2**(-17)

G = 0.1 # Свободный параметр

x_max, iterations, final_a, final_b = search_with_dichotomy(a, b, e, G)

print(f"Максимум функции достигается в точке x = ", x_max)

print(f"Количество итераций: ", iterations)

print(f"Итерации завершились на интервале [{final_a}, {final_b}]")

Рисунок 3- Максимум функции, число итераций и конечный интервал

Для нахождения экстремума функции алгоритму потребовалось 19 итераций.

Реализован метод золотого сечения (Листинг 3). Данный метод обеспечивает, что каждая итерация приводит к уменьшению интервала на фиксированное соотношение. Каждая новая длина интервала составляет ​ 61,8 % от предыдущей длины.

Листинг 3- Реализация метода золотого сечения

def f(x):

return -x**2 - 10*x + 5

def search_with_golden_section(a, b, e):

phi = (np.sqrt(5)+1) / 2

iteration = 0

interval_length = b - a

while interval_length > e:

iteration += 1

x1 = b - (b - a) / phi

x2 = a + (b - a) / phi

f_x1 = f(x1)

f_x2 = f(x2)

if f_x1 < f_x2:

a = x1

else:

b = x2

interval_length = b - a

return (a + b) / 2, iteration, a, b

a = -6.6

b = -4

e = 2**(-17)

x_max, iterations, final_a, final_b = search_with_golden_section(a, b, e)

print(f"Максимум функции достигается в точке x = ", x_max)

print(f"Количество итераций: ", iterations)

print(f"Итерации завершились на интервале [{final_a}, {final_b}]")

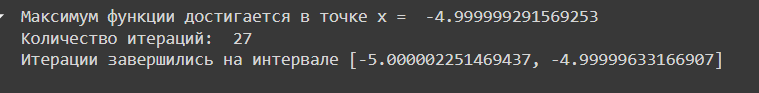
Рисунок 4- Максимум функции, число итераций и конечный интервал

Далее реализован Метод Фибоначчи, который основан на использовании последовательности Фибоначчи для сужения интервала (Листинг 4).

Листинг 4- Реализация метода Фибоначчи

def f(x):

return -x**2 - 10*x + 5

def fibonacci_search(a, b, e):

# построение ряда

fib = [1, 1]

while fib[-1] < (b - a) / e:

fib.append(fib[-1] + fib[-2])

n = len(fib) - 1 # количество итераций

x1 = a + (fib[n-2] / fib[n]) * (b - a)

x2 = a + (fib[n-1] / fib[n]) * (b - a)

f_x1, f_x2 = f(x1), f(x2)

for i in range(n-1):

if f_x1 < f_x2:

a = x1

x1, f_x1 = x2, f_x2

x2 = a + (fib[n-i-1] / fib[n-i]) * (b - a)

f_x2 = f(x2)

else:

b = x2

x2, f_x2 = x1, f_x1

x1 = a + (fib[n-i-2] / fib[n-i]) * (b - a)

f_x1 = f(x1)

return (a + b) / 2, n

a = -6.6

b = -4

e = 2**(-17)

x_max, iterations = fibonacci_search(a, b, e)

print(f"Максимум функции достигается в точке x = {x_max}")

print(f"Количество итераций: {iterations}")

Рисунок 5- Максимум функции, число итераций

Для сравнения алгоритмов поиска экстремума построен график зависимости числа итераций от погрешности (Рисунок 6).

Листинг 5 – Создание графика

iterations_1 = [search_algorithm(a, b, N, e)[1] for e in e_values]

iterations_dichotomy = [search_with_dichotomy(a, b, e, G)[1] for e in e_values]

iterations_golden = [search_with_golden_section(a, b, e)[1] for e in e_values]

iterations_fibonacci = [fibonacci_search(a, b, e)[1] for e in e_values]

plt.figure(figsize=(10, 6))

plt.plot(e_values, iterations_1, label='Равномерный поиск')

plt.plot(e_values, iterations_dichotomy, label='Дихотомия')

plt.plot(e_values, iterations_golden, label='Золотое сечение')

plt.plot(e_values, iterations_fibonacci, label='Фиббоначи')

plt.xscale('log', base=2)

plt.xlabel('E')

plt.ylabel('Количество итераций')

plt.title('Зависимость числа итераций от погрешности')

plt.legend()

plt.grid(True)

plt.show()

Рисунок 6- График зависимости числа итераций от погрешности

Вывод: изучены алгоритмы поиска экстремума унимодальной функции. Самым быстрым алгоритмом оказался метод равномерного поиска, который выполнил задачу за пять итераций.