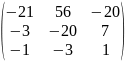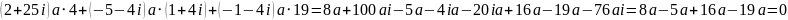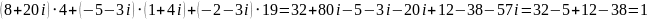ГУАП
КАФЕДРА №
ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
доц., канд. техн. наук |
|
|
|
Д.Ю.Волков |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
ОТЧЕТ О ПРАКТИЧЕСКИХ ЗАДАНИЯХ |
|
по курсу: МАТЕМАТИКА, АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА |
|
|
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № |
4116 |
|
|
|
|
|
|
|
подпись, дата |
|
инициалы, фамилия |
Санкт-Петербург 202
1.Решить функцию подставив вместо x матрицу A.
A=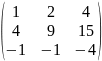 f(x)=-1-20x-6x2+x3;
f(A)=?
f(x)=-1-20x-6x2+x3;
f(A)=?
Варианты ответа:
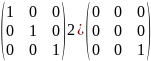 3)
3)
 4) нет правильного ответа
4) нет правильного ответа
Решение:
Найдем f(A) :
f(A)=-1⨯ℰ-20A-6A2+A3,
где ℰ-это единичная матрица;
-1⨯ℰ=-1⨯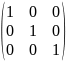 =
=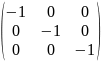
чтобы перемножить матрицы, нужно умножить элементы в строках первой матрицы на элементы в столбцах второй матрицы и сложить полученные значения.
A2= ⨯ =
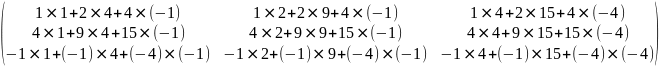 =
=
=
A3=
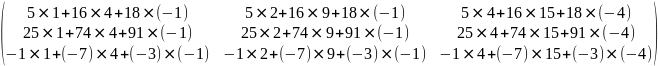 =
=
=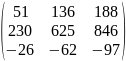
20A=20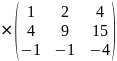 =
=
6A2=
6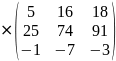 =
=
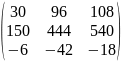
Подставляем матрицы в f(A)=-1⨯ℰ-20A-6A2+A3
- - +
=
2.
Возведите комплексное число в степень:
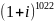
Варианты ответов:
 2)
2)
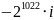 3)
3)
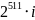 4)
нет правильного варианта ответа
4)
нет правильного варианта ответа
Решение:
Чтобы
возвести комплексное число
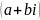 в степень нужно представить его в
тригонометрической форме
в степень нужно представить его в
тригонометрической форме

где
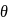 =
arctg(
=
arctg(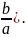
И
возвести его в степень n:
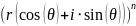 =
=

Представим
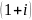 в тригонометрической форме:
в тригонометрической форме:
Найдём его модуль
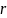 =|
=| =
=
 =
=

Поскольку действительная часть больше нуля (1>0) и мнимая часть больше нуля (1>0), значит :
=
arctg( arctg
arctg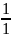 =arctg
1=
=arctg
1=
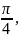
Таким образом, тригонометрическая форма комплексного числа
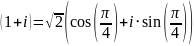
Далее возводим его в степень
 =
=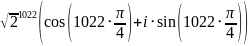 =
=
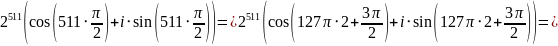
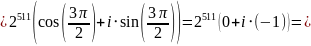
=
3. Даны две матрицы A и B, найдите значение параметра а при котором определитель произведения матриц A и B равен 1.
A= , B=
, B=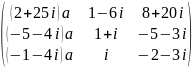 .
.
Варианты ответов:
1)0 2)1 3)-1 4) нет правильного варианта ответа
Решение:
Перемножим матрицы построчно:
строка
 ,
так как
,
так как
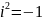 ,
то
,
то
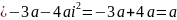
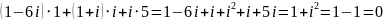

Строка:
Строка:
3.1.
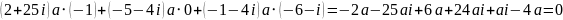
3.2.

3.3.
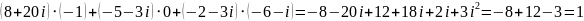
Таким образом мы получили матрицу:

Найдём её определитель:
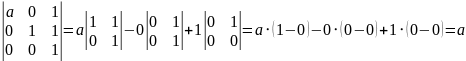
Поскольку нам нужно, чтобы определитель равнялся 1, значит a=1.
Решить систему уравнений методом Крамера
6x+24y= -18
9x+37y= -28
Варианты ответов:
(1;-1) 2) (1;1) 3(-1;1) 4) нет правильного ответа
Решение:
Чтобы решить систему, нужно вычислить определитель матрицы системы:
По теореме Крамера, если определитель матрицы квадратной системы ненулевой, значит система совместна и у неё есть одно решение и его можно найти по формулам Крамера.
(Δ - определитель матрицы системы)
Δ=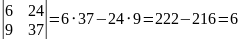
Т.к. Δ≠0, значит из теоремы Крамера система имеет одно решение. Вычисляем дополнительные определители. Определитель Δ1 получаем из определителя Δ, заменяя первый столбец столбцом свободных коэффициентов:
Δ1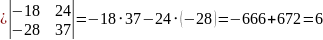
Также получаем определитель Δ2 из определителя матрицы системы, заменяем второй столбец столбцом свободных коэффициентов:
Δ2=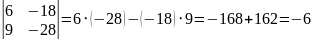
Получаем:
x=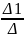 =
=
 y=
y=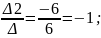
ответ: (1;-1).
Проверка:

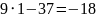
Решить систему уравнений с помощью метода подстановки и метода Крамера.
x+5y+5z= -9
4x+21y+19z= -36
x+9y+2z= -10
Варианты ответов:
1)(1;0;1) 2)(1;-1;1) 3)(1;-1;-1) 4) Нет правильного варианта ответа.
Чтобы решить систему, нужно вычислить определитель матрицы системы:
По теореме Крамера, если определитель матрицы квадратной системы ненулевой, значит система совместна и у неё есть одно решение и его можно найти по формулам Крамера.
(Δ - определитель матрицы системы)
Δ=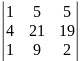 =
= =
=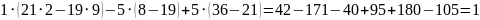 .
.
Т.к. Δ≠0, значит из теоремы Крамера система имеет одно решение. Вычисляем дополнительные определители. Определитель Δ1 получаем из определителя Δ, заменяя первый столбец столбцом свободных коэффициентов:
Δ1=
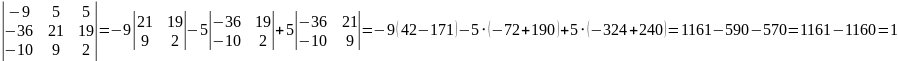 .
.
Также получаем определитель Δ2 из определителя матрицы системы, заменяем второй столбец столбцом свободных коэффициентов:
Δ2=
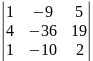 =
=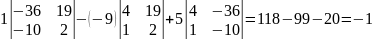 .
.
И находим Δ3 из определителя матрицы системы, заменяя третий столбец столбцом свободных коэффициентов:
Δ3=
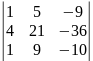 =
=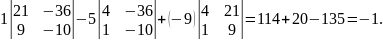
Получаем:
x=
=
 y=
y=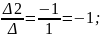 z=
z=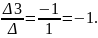
ответ:(1; -1; -1).
выполним проверку:
1-5-5=-9
4-21-19=-36
1-9-2=-10.
Дана пирамида ABCD.
Найти площадь граней с помощью векторного произведения.
Найти объём с помощью смешанного произведения.
Найти длины высот с помощью объёма и площади грани.
найти уравнения плоскостей граней, сделать проверку полученных уравнений.
A(1, -2, 1) , B(2, 0, 3) C(4, 1, 1), D(-2, -8,4).
Решение:
найдём площади граней пирамиды:
чтобы найти площадь граней пирамиды, для начала, найдём координаты векторов:
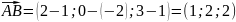
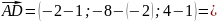
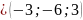
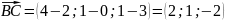

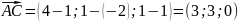
Затем находим векторное произведение:
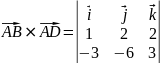 =
=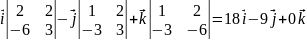 .
.
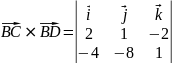 =
= .
.
 =
= .
.
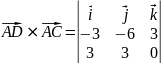 =
=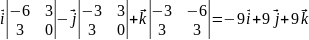 .
.
Далее вычисляем длину векторного произведения и находим площадь граней:

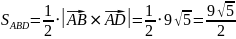
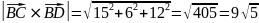
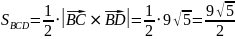


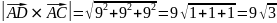
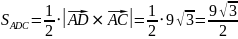
найдём
объём пирамиды с помощью смешанного
произведения:
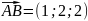 ,
,
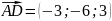 ,
,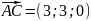
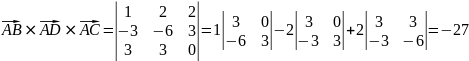
Таким образом,
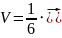
3. с помощью объёма и площади найдём длины высот пирамиды ABCD.
Так,
как
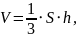 значит
значит
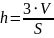
Найдём высоту на грань BAC:
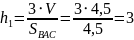
Найдём высоту на грань CBD:
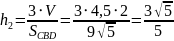
Найдём высоту на грань DBA:
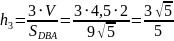
Найдём высоту на грань DAC:
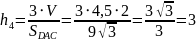
4.) найдём уравнения плоскостей граней:
Возьмём
произвольную точку М(x;y;z),
эта точка принадлежит плоскости тогда,
когда вектор
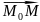 перпендикулярен
вектору
перпендикулярен
вектору
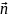 (вектору
нормали), для этого необходимо, чтобы
скалярное произведение этих векторов
было равно нулю:
(вектору
нормали), для этого необходимо, чтобы
скалярное произведение этих векторов
было равно нулю:
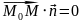
Грань ABC:
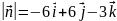 .
.
Значит,
имеет координаты (-6;6;-3), пусть
 , тогда
, тогда
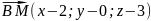 ,
т.к.
,
т.к.
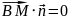 ,значит:
,значит:
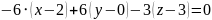
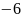 x+12+6y-3z+9=0
x+12+6y-3z+9=0
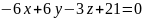
Выполним проверку:
Для
точки А(1;-2;1):
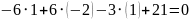
Для
точки C(4;1;1):
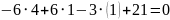
Грань DAC:
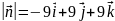 .
.
Значит,
имеет координаты (-9;9;9), пусть
 , тогда
, тогда
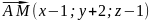 ,
т.к.
,
т.к.
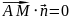 ,значит:
,значит:
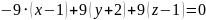
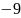 x+9+9y+18+9z-9=0
x+9+9y+18+9z-9=0
x+9y+9z+18=0
Выполним проверку:
Для
точки D(-2;-8;4):
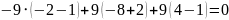
Для
точки C(4;1;1):

Грань DBA:
 .
.
Значит,
имеет координаты (18;-9;0), пусть
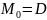 , тогда
, тогда
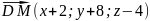 ,
т.к.
,
т.к.
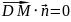 ,значит:
,значит:
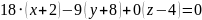
 x+36-9y-72+0z-0=0
x+36-9y-72+0z-0=0

Выполним проверку:
Для
точки А(1;-2;1):
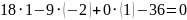
Для
точки B(2;0;3):

Грань CBD:
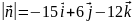 .
.
Значит,
имеет координаты (-15;6;-12), пусть
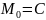 , тогда
, тогда
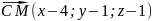 ,
т.к.
,
т.к.
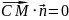 ,значит:
,значит:

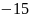 x+60+6y-6-12z+12=0
x+60+6y-6-12z+12=0
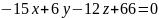
Выполним проверку:
Для
точки B(2;0;3):

Для
точки D(-2;-8;4):
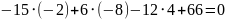
найти обратную матрицу с помощью элементарных преобразований:

Варианты ответов:
1)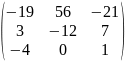 2)
2)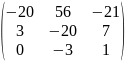 3)
3)