15300

Задача 15300

Найти напряженность магнитного поля в центре кругового витка радиусом 9 см, помещенного в квадратную рамку со стороной 18 см так, что их плоскости совпадают, а направления токов в них силой 20 А противоположны.

r = 9 см = 0,09 м a = 18 см = 0,18 м I = 20 А	Индукция магнитного поля в центре кругового проводника с током где μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, μ ― магнитная проницаемость среды, для воздуха μ = 1. I ― сила тока в проводнике, r ― радиус проводника.
B ― ?

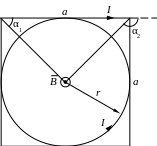
Магнитная индукция поля, создаваемая отрезком проводника

где b ― расстояние до оси проводника,

α₁ и α₂ ― углы между направлением тока и направлением на точку, в которой создано магнитное поле, вершинами которых являются соответственно начало и конец прямого участка проводника. Из рисунка:

Тогда

Учитывая симметрию квадрата, все стороны создают в центре поля с одинаковыми индукциями B₂. По принципу суперпозиции полей находим результирующий вектор магнитной индукции в центре квадрата:

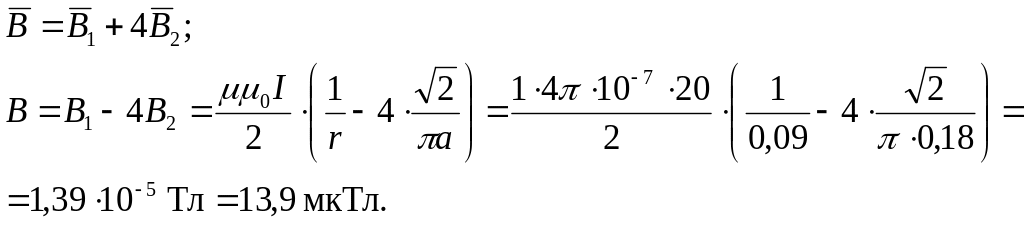
Ответ: B = 13,9 мкТл.