24. Вопросно-ответные процедуры : характеристика ответа, виды. Логические требования к построению ответов.

Ответ - это суждение, вызванное вопросом. Основными функциями ответа являются: а) уменьшение неопределенности, заключенной в вопросе, или б) указание на неправильную постановку вопроса. виды ответов.

1. По области поиска ответы делятся на прямые и косвенные. Прямым называется ответ, который берется непосредственно из области поиска ответов, без дополнительных сведений или рассуждений. Косвенный ответ берется из более широкой области, нежели область поиска ответов, он связан с прямым ответом некоторым логическим отношением по истинности. Например, на вопрос «Совершал ли гражданин Кузин данное преступление?» можно ответить: «В то время, когда было совершено преступление, гражданин Кузин вместе со своей семьей находился в другом городе в гостях у родственников». Этот ответ является косвенным.

2. По объему информации различают полные и частичные ответы. Полный ответ без остатка устраняет сообщаемую вопросом неопределенность и делает неизвестное известным. Частичный ответ только в некоторой степени устраняет сообщаемую вопросом неопределенность и приближает превращение неизвестного в известное. Им является всякое суждение, вытекающее в качестве следствия из прямого ответа на основе принятых положений, но не наоборот. Например, на вопрос «Готово ли правительство твердо взять власть в свои руки и осуществить экономическую реформу?» депутат ответил: «Правительство не может осуществить экономическую реформу, так как не разработана ее концепция». Ответ частичный: нет ответа на первую часть вопроса.

правила формулирования ответа:

1. Ответ должен быть ясным, однозначным и кратким. Это во многом зависит от того, как отвечающий понимает вопрос и хочет ли он на него давать ответ.

2. Ответ должен уменьшать неопределенность вопроса, быть информативнее его. Многие споры и дискуссии бесплодны в силу отступления от этого правила. «Толкут воду в ступе» — говорят в таких случаях.

3. При некорректной постановке вопроса ответ должен содержать и указание на эту некорректность. В некоторых случаях достаточно сказать, что в таком-то пункте вопрос не ясен и требует уточнения. В других - что вопрос не заслуживает обсуждения, поскольку он окончательно решен и ответ известен. В третьих - что требовать ответа пока преждевременно, поскольку вопрос неразрешим в силу недостатка каких-то данных, отсутствия подходящих методов решения и т. д. Особого внимания заслуживают вопросы, источник некорректности которых - ложность их предпосылок. Единственно возможный способ отвечать на такие вопросы - отвергать эти ложные предпосылки.

Таким образом, вопросно-ответный комплекс играет важную роль в процессе познания правовой действительности. Поэтому юристу нужно знать логическую сущность вопросов и ответов, их виды, правила постановки вопросов, чтобы корректно их задавать и отвечать на них, различая и указывая уловки, которые могут применить собеседники по незнанию или преднамеренно.

25. Понятие формулы. Тождественно-истинные , тождественно-ложные, выполнимые формулы.

Законом логики или тождественно-истинной формулой (тавтологией) называется формула, которая принимает значение истинности при  любых значениях входящих в нее переменных. Например: ((а→b)Λb c черточкой) → ā. Каждая тождественно-истинная формула выражает какой-то логический закон. Все тождественно-истинные формулы равносильны друг другу. Существуют также формулы, которые при любых наборах логических значений переменных получают в заключительном столбце своей таблицы логическое значение "ложь". Они называются тождественно-ложными (противоречивыми) формулами. Тождественно-ложные формулы равносильны друг другу. Формулы, которые могут принимать как истинные значения, так и ложные называются промежуточными или выполнимыми. Тождественно истинные формулы (или тавтологии) -это особый класс формул исчисления предикатов, которые принимают значение “истины”  для всех интерпретаций входящих в нее предметных постоянных, функциональных и предикатных символов; эти формулы играют роль законов и аксиом исчисления предикатов; любые подстановки и замещения в тождественно истинной формуле не изменяют ее значения. Тождественно ложные формулы (или противоречие)-это особый класс формул исчисления предикатов, которые принимают значение “ложь” для всех интерпретаций входящих в нее предметных постоянных, функциональных и предикатных символов; любые подстановки и замещения в тождественно ложной формуле не изменяют ее значения. Выполнимые формулы - это особый класс формул исчисления предикатов, которые принимают значение “истина”в некоторой области, т.е. не для всех интерпретаций входящих в нее предметных постоянных, функциональных и предикатных символов.

26. Дедуктивное умозаключение. Характер логического следования в дедуктивных умозаключениях.  Дедуктивное умозаключение (от лат. deductio - выведение) - такое умозаключение, в котором переход от общего знания к частному является логически необходимым. Путем дедукции получаются достоверные выводы: если истинны посылки, то будут истинны и заключения. Пример:Если человек совершил преступление, то он должен быть наказан. Петров совершил преступление. Петров должен быть наказан. Истинность заключения при истинности посылок в дедуктивных умозаключениях обусловливается тем, что в этих умозаключениях между посылками и заключением существует отношение логического следования, которое можно определить следующим образом: из суждения α логически следует суждение β тогда и только тогда, когда α и β связаны по смыслу, а α→β является логическим законом. Умозаключение будет дедуктивным, если его символическое выражение будет представлять собой логический закон, т. е. тождественно-истинную формулу, что проверяется посредством таблицы истинности. 

В силу того, что в дедуктивных умозаключениях заключение логически следует из посылок, они представляют собой самый надёжный способ доказательства. Однако надёжность дедуктивных умозаключений существует в ущерб их информативности, то есть они не дают новой информации о мире. В заключениях этих умозаключений содержится та же самая информация, что и в посылках, и нет никакой новой информации. Поэтому выводы данного типа достоверны: если истинна информация в посылках, то истинна и та её часть, которая содержится (выводится) в заключении. 27. Непосредственное умозаключение. (умозаключение по логическому квадрату) Непосредственные умозаключения - такие, в которых заключение выводится из одной посылки. Например, из суждения «Все адвокаты - юристы» можно получить новое суждение «Некоторые юристы - адвокаты». Непосредственные умозаключения дают нам возможность выявить знание о таких сторонах предметов, которое уже содержалось в исходном суждении, но не было явно выражено и явно осознано. В этих условиях мы делаем неявное - явным, неосознанное - осознанным. К непосредственным умозаключениям относятся: превращение, обращение, противопоставление предикату, умозаключение по «логическому квадрату». Умозаключение по «логическому квадрату». «Логический квадрат» - это схема, выражающая истинностные отношения между простыми суждениями, имеющими один и тот же субъект и предикат. В данном квадрате вершины символизируют известные нам по объединенной классификации простые категорические суждения: А, Е, О, I. Стороны и диагонали можно рассматривать как логические отношения между простыми суждениями (кроме эквивалентных). Так, верхняя сторона квадрата обозначает отношение между А и Е - отношение противоположности; нижняя сторона -отношение между О и I - отношение частичной совместимости. Левая сторона квадрата (отношение между А и I) и правая сторона квадрата (отношение между Е и О) - отношение подчинения. Диагонали обозначают отношения между А и О, Е и I, которые называются противоречием. 1. Отношение противоположности имеет место между суждениями общеутвердительными и общеотрицательными (А-Е). Сущность этого отношения состоит в том, что два противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Поэтому если одно из противоположных суждений истинно, то другое непременно ложно, но если одно из них ложно, то о другом суждении еще нельзя безоговорочно утверждать, что оно истинно, - оно неопределенно, т. е. может оказаться как истинным, так и ложным. Например, если истинно суждение «Всякий адвокат является юристом», то противоположное ему суждение «Ни один адвокат не является юристом» будет ложно. Но если ложно суждение «Все студенты нашего курса раньше изучали логику», то противоположное ему «Ни один студент нашего курса раньше не изучал логику» будет неопределенным, т. е. оно может оказаться как истинным, так и ложным. 2. Отношение частичной совместимости имеет место между суждениями частноутвердительными и частноотрицательными (I - О). Такие суждения не могут быть одновременно ложными (по крайней мере одно из них истинно), но могут быть одновременно истинными. Например, если ложно суждение «Иногда можно опаздывать на урок», то суждение «Иногда нельзя опаздывать на урок» будет истинным. Но если одно из суждений истинно, то другое суждение, находящееся с ним в отношении частичной совместимости, будет неопределенным, т.е. оно может оказаться как истинным, так и ложным. Например, при истинности суждения «Некоторые люди изучают логику» суждение «Некоторые люди не изучают логику» будет истинным или ложным. Но при истинности суждения «Некоторые атомы делимы» суждение «Некоторые атомы не являются делимыми» будет ложным. 3. Отношение подчинения существует между общеутвердительными и частноутвердительными суждениями (А-I), а также между общеотрицательными и частноотрицательными суждениями (Е-О). При этом А и Е являются подчиняющими, а I и О - подчиненными суждениями. Отношение подчинения состоит в том, что из истинности подчиняющего суждения обязательно следует истинность подчиненного суждения, но обратное необязательно: при истинности подчиненного суждения подчиняющее будет неопределенным - оно может оказаться как истинным, так и ложным. Но если подчиненное суждение ложно, то подчиняющее будет тем более ложным. Обратное опять-таки необязательно: при ложности подчиняющего суждения подчиненное может оказаться как истинным, так и ложным. Например, при истинности подчиняющего суждения «Все адвокаты - юристы» подчиненное суждение «Некоторые адвокаты - юристы» будет тем более истинным. Но при истинности подчиненного суждения «Некоторые адвокаты входят в Московскую коллегию адвокатов» подчиняющее суждение «Все адвокаты входят в Московскую коллегию адвокатов» будет ложным или истинным. При ложности подчиненного суждения «Некоторые адвокаты не входят в Московскую коллегию адвокатов» (О) будет ложным подчиняющее суждение «Ни один адвокат не входит в Московскую коллегию адвокатов» (Е). Но при ложности подчиняющего суждения «Ни один адвокат не входит в Московскую коллегию адвокатов» (Е) подчиненное суждение «Некоторые адвокаты не входят в Московскую коллегию адвокатов» (О) будет истинным или ложным. 4. Отношения противоречия существует между общеутвердительными и частноотрицательными суждениями (А - О) и между общеотрицательными и частноутвердительными суждениями (Е - I). Сущность этого отношения состоит в том, что из двух противоречающих суждений одно обязательно истинно, другое - ложно. Два противоречивых суждения не могут быть ни одновременно истинными, ни одновременно ложными. Умозаключения, основанные на отношении противоречия, называются отрицанием простого категорического суждения. С помощью отрицания суждения из исходного суждения образуется новое суждение, являющееся истинным, когда исходное суждение (посылка) ложно, и ложным, когда исходное суждение (посылка) истинно. Например, отрицая истинное суждение «Все адвокаты - юристы» (А), мы получим новое, ложное, суждение «Некоторые адвокаты не есть юристы» (О). Отрицая ложное суждение «Ни один адвокат не юрист» (Е), мы получим новое, истинное, суждение «Некоторые адвокаты - юристы» (I). Знание зависимости истинности или ложности одних суждений от истинности или ложности других суждений помогает делать правильные выводы в процессе рассуждения. 30. Непосредственное умозаключение (обращение, правила, схемы). Обращение - такое непосредственное умозаключение, в котором происходит перемена мест субъекта и предиката при сохранении качества суждения. Обращение подчиняется правилу распределенности терминов: если термин не распределен в посылке, то он не должен быть не распределен и в заключении. Если обращение ведет к изменению исходного суждения по количеству (из общего исходного получается новое частное суждение), то такое обращение называется обращением с ограничением; если обращение не ведет к изменению исходного суждения по количеству, то такое обращение является обращением без ограничения. Примеры и схемы обращения: А: Общеутвердительное суждение обращается в частноутвердительное.

Все адвокаты - юристы. Некоторые юристы - адвокаты. Все S суть Р. Некоторые Р суть S. Общеутвердительные выделяющие суждения обращаются без ограничения. Всякое правонарушение (и только правонарушение) суть противоправное деяние. Всякое противоправное деяние суть правонарушение. Схема: Все S, и только S, суть Р. Все Р суть S. Е: Общеотрицательное суждение обращается в общеотрицательное (без ограничения). Ни один адвокат не судья. Ни один судья не адвокат. Ни один S не есть Р. Ни один Р не есть S. I: Частноутвердительные суждения обращаются в частноутвердительные. Некоторые юристы - спортсмены. Некоторые спортсмены - юристы. Некоторые S суть Р. Некоторые Р суть S. Частноутвердительные выделяющие суждения обращаются в общеутвердительные: Некоторые юристы, и только юристы, являются адвокатами. Все адвокаты суть юристы. Некоторые S, и только S, суть Р. Все Р суть S. О: Частноотрицательные суждения не обращаются. Логическая операция обращения суждения имеет большое практическое значение. Незнание правил обращения приводит к грубым логическим ошибкам. Так, довольно часто общеутвердительное суждение обращается без ограничения. Например, суждение «Все юристы должны знать логику» обращается в суждение «Все изучающие логику - юристы». Но это неверно. Верно суждение «Некоторые изучающие логику - юристы». 31. Непосредственное умозаключение (превращение, правила, схемы). Превращение - такое умозаключение, в котором исходное суждение преобразуется в новое суждение, противоположное по качеству, и с предикатом, противоречащим предикату исходного суждения. Чтобы превратить суждение, надо изменить его связку на противоположную, а предикат - на противоречащее понятие. Если посылка выражена не в явной форме, то надо преобразовать ее в соответствии со схемами суждений А, Е, I, О. Если посылка записана в форме суждения «Не все S суть Р» , то его надо преобразовать в частноотрицательное: «Некоторые S не суть Р». Примеры и схемы превращения: А:Все студенты первого курса изучают логику. Ни один студент первого курса не изучает не логику. Схема: Все S суть Р. Ни одно S не суть не-Р. Е: Ни одна кошка не является собакой. Всякая кошка является не-собакой. Ни один S не есть Р. Все S есть не-Р. I: Некоторые адвокаты суть спортсмены. Некоторые адвокаты не суть не-спортсмены. Некоторые S суть Р. Некоторые S не суть не-Р. О: Некоторые адвокаты не суть спортсмены. Некоторые адвокаты суть не-спортсмены. Некоторые S не суть Р. Некоторые S суть не-Р. 32. Непосредственное умозаключение (противопоставление предикату, противопоставление субъекту, правила, схемы). Противопоставление предикату - это последовательное применение операций превращения и обращения - преобразование суждения в новое суждение, в котором субъектом становится понятие, противоречащее предикату, а предикатом - субъект исходного суждения; меняется качество суждения. Например, из суждения «Все адвокаты - юристы» можно, противопоставляя предикат, получить «Ни один не-юрист не является адвокатом». Схематически: Все S суть Р. Ни одно не- Р не есть S 1) для общеутвердительного суждения: Все S есть Р. Ни одно не-Р не есть S. 2) для общеотрицательного суждения: Ни одно S не есть Р. Некоторые не-Р есть S. 3) для частноотрицательного суждения: Некоторые S не есть Р. Некоторые не-Р есть S. 4) для частноутвердительных суждений нельзя проводить вывод путем противопоставления предикату, так как после превращения исходного суждения получается частноотрицательное суждение, для которого не применяется операция обращения. Пример. Противопоставление предикату для частноотрицательного суждения «Некоторые озера не имеют стока»: Некоторые водоемы, являющиеся озерами (S), не есть водоемы, имеющие сток (Р). Некоторые водоемы, не имеющие стока (не-Р), есть водоемы, являющиеся озерами (S). Противопоставление субъекту - это преобразование категорического суждения, в результате которого субъектом становится предикат исходного суждения, а предикатом - понятие, противоречащее субъекту исходного суждения. Такой вывод можно осуществить, последовательно применяя обращение исходного суждения, а затем - превращение полученного результата, либо сразу следуя правилам для противопоставления субъекту: 1) для общеутвердительного суждения: Все S есть Р. Некоторые Р не есть не-S. 2) для общеотрицательного суждения: Ни одно S не есть Р. Все Р есть не-S. 3) для частноутвердительного суждения: Некоторые S есть Р. Некоторые Р не есть не-S. 4) для частноотрицательных суждений не используются выводы с применением противопоставления субъекту, так как в процессе этого вывода мы должны были бы сделать обращение частноотрицательного суждения, для которого не применяется вывод посредством обращения. Пример. «Ни один злой человек не может быть вполне справедливым». Это общеотрицательное суждение (Е). Приводя его к логической форме («Ни одно S не есть Р»), делаем вывод в соответствии с формой противопоставления субъекту для общеотрицательного суждения: Ни один человек, являющийся злым (S), не есть человек, который может быть вполне справедливым (Р). Все люди, которые могут быть вполне справедливыми (Р), есть люди, не являющиеся злыми (не-S).  31. Простой категорический силлогизм. Состав, фигуры. Простой категорический силлогизм (простое дедуктивное умозаключение) - такое умозаключение, в котором заключение и посылки являются простыми категорическими суждениями. Категорические суждения - такие, в которых мысль утверждается или отрицается вполне определенно, без всяких условий, и которые имеют субъектно-предикатную структуру. Пример:Все адвокаты - юристы. Петров - адвокат. Петров - юрист. Проанализируем структуру силлогизма. Понятия, входящие в состав силлогизма, называются терминами силлогизма. Различают меньший, больший и средний термины. Меньший термин - понятие, которое в заключении является субъектом (в нашем примере - понятие «Петров») и обозначается буквой «S». Больший термин - понятие, которое в заключении является предикатом («юрист») и обозначается «Р». Средний термин - понятие, которое входит в обе посылки и не входит в заключение («адвокат»), обозначается буквой «М» (от лат. medium - средний). Схема силлогизма: Все М есть Р. S есть М. S есть Р. Каждая из посылок имеет свое название: та посылка, в которую входит больший термин, называется большей посылкой. Та, в которую входит меньший термин, называется меньшей посылкой. В посылках дано отношение меньшего и большего терминов к среднему термину. В заключении устанавливается отношение между меньшим и большим терминами. Фигуры и правила фигур силлогизма. В зависимости от места среднего термина в посылках различают четыре фигуры категорического силлогизма. Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например: Все газы (М) – это химические элементы (Р). Гелий (S) – это газ (М). Гелий (S) – это химический элемент (Р). Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Например: Все рыбы (Р) дышат жабрами (М). Все киты (S) не дышат жабрами (М). Все киты (S) не рыбы (Р). Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например: Все тигры (М) – это млекопитающие (Р). Все тигры (М) – это хищники (S). Некоторые хищники (S) – это млекопитающие (Р). Четвёртая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например: Все квадраты (Р) – это прямоугольники (М). Все прямоугольники (М) – это не треугольники (S). Все треугольники (S) – это не квадраты (Р). В четырех фигурах силлогизма максимальное число комбинаций равно 64. Однако правильных модусов всего 19: Первая фигура: ААА, ЕАЕ, АII, ЕIО Вторая фигура: ЕАЕ, АЕЕ, ЕIО, АОО Третья фигура: AAI, IAI, АII, ЕАО, ОАО, ЕIО Четвертая фигура: AAI, АЕЕ, IAI, ЕАО, ЕIО В соответствии с этим называют модусы первой фигуры, модусы второй фигуры и т. д. Например, модус ААА 1-й фигуры, модус АЕЕ 2-й фигуры и т.д. Все другие модусы возможны, но они являются неправильными, так как в них нарушаются те или иные правила категорического силлогизма. Знание модусов дает возможность определить форму истинного заключения, когда даны посылки и известно, какова фигура данного силлогизма. 32. Общие правила силлогизма. Правила для терминов. 1. В силлогизме должно быть только три термина. Нарушение этого правила связано с отождествлением разных понятий, которые принимаются за одно и рассматриваются как один термин. Ошибка: «учетверение терминов». Мышь грызет книжку. Мышь - имя существительное. Имя существительное грызет книжку. Ошибка связана с тем, что слово «мышь» выражает различные понятия (имеет разный смысл). 2. Средний термин должен быть распределен хотя бы в одной из посылок. Если средний термин не распределен ни в одной из посылок, то связь между крайними терминами остается неопределенной. Некоторые растения (М-) ядовиты (Р). Белые грибы (S) - растения (М-). Белые грибы (S) - ядовиты (Р). Средний термин не распределен ни в одной из посылок. Поэтому необходимую связь между терминами нельзя установить. 3. Термин, не распределенный в посылке, не может быть распределен в заключении. Ошибка: «незаконное распределение меньшего (или большего) термина». Во всех городах за полярным кругом (М) бывают белые ночи (Р-). Санкт-Петербург (S) не находится за Полярным кругом (М). В Санкт-Петербурге (S) не бывает белых ночей (Р+). Заключение ложное, так как нарушено данное правило. Предикат (Р) в посылке не распределен, а в заключении - распределен. Следовательно, произошло расширение большего термина. 33. Общие правила силлогизма. Правила для посылок. 1. Хотя бы одна из посылок должна быть утвердительным суждением. Адвокаты не судьи. Студенты не адвокаты. ? 2. Если одна из посылок - отрицательное суждение, то и заключение - отрицательное суждение. Все адвокаты юристы. Петров не юрист. Петров не адвокат. 3. Хотя бы одна из посылок должна быть общим суждением. Некоторые юристы спортсмены. Некоторые юристы любят музыку. ? 4. Если одна из посылок частная, то и заключение должно быть частным. Все преступники должны быть наказаны. Некоторые люди - преступники. Некоторые люди должны быть наказаны. 34. Правила фигур простого категорического силлогизма. Первая фигура - разновидность силлогизма, в которой средний термин занимает место субъекта в большей посылке (М - Р) и место предиката в меньшей посылке (S - М). Например: Все адвокаты (М) - юристы (Р) Петров (S) - адвокат (М). Петров (S) - юрист (Р). М-Р - большая посылка. S - М - меньшая посылка. S — Р - заключение. Правила первой фигуры: Ø большая посылка должна быть общим суждением (А, Е); Ø меньшая посылка должна быть утвердительным суждением (А, I). Первая фигура силлогизма широко применяется в юридической науке и практике. Так, по первой фигуре производится квалификация различных правовых явлений, преступлений, фактов судебной практики. При этом большей посылкой выступает та или иная статья кодекса, правовая норма, закон, а меньшей - рассматриваемый конкретный случай. В заключении делается вывод о рассматриваемом случае на основании общего положения. Например, «Тайное хищение чужого имущества составляет кражу. Данный человек совершил тайное хищение чужого имущества. Следовательно, данный человек совершил кражу». Вторая фигура - разновидность простого силлогизма, в которой средний термин занимает место предиката в обеих посылках. Например: Все адвокаты (М) - юристы. Петров - не юрист (М). Петров - не адвокат. Р - М - большая посылка. S - М - меньшая посылка. S — Р - заключение. Правила второй фигуры: Ø большая посылка должна быть общим суждением (А, Е); Ø одна из посылок должна быть отрицательной (Е, О). Вторая фигура применяется при доказательствах ложности какого-либо положения путем отрицания принадлежности исследуемых предметов к классу предметов, о которых мыслится в большей посылке. В судебной практике данная фигура служит для логического обоснования отсутствия состава преступления в том или ином конкретном деянии, для доказательства неправильной квалификации преступления, для опровержения каких-либо положений, не согласующихся с общим правилом. Например, «Этот смертельный удар нанесен человеком, обладающим огромной физической силой. Обвиняемый не является человеком, обладающим огромной физической силой. Следовательно, обвиняемый не мог нанести этот смертельный удар». Третья фигура - разновидность силлогизма, в которой средний термин занимает место субъекта в обеих посылках (М - Р; М - S). Например: Все подозреваемые (М) признали свою вину. Все подозреваемые (М) привлечены к уголовной ответственности. Некоторые привлеченные к уголовной ответственности, признали свою вину. М - Р - большая посылка. М - S - меньшая посылка. S - Р - заключение. Правила третьей фигуры: Ø меньшая посылка должна быть утвердительным суждением (А, I); Ø о заключение должно быть частным суждением (I, О). Третья фигура служит чаще всего для установления частичной совместимости признаков, относящихся к одному и тому же предмету. Она также может быть применима для опровержения отдельных общих положений. Например, необходимо опровергнуть суждение «Ни один свидетель не дал правдивых показаний» (т. е. доказать противоречащее ему суждение «Некоторые свидетели дали правдивые показания») и известно, что свидетели X. и Y. дали правдивые показания. Построим умозаключение по третьей фигуре: X. и Y. (М) - дали правдивые показания. X. и Y. (M) - свидетели. Некоторые свидетели дали правдивые показания. P - M- большая посылка. S - M - меньшая посылка. S-P- заключение. Поскольку частноутвердительное суждение «Некоторые свидетели дали правдивые показания» является истинным, то находящееся с ним в отношении противоречия общеотрицательное суждение «Ни один свидетель не дал правдивых показаний» - ложное. Четвертая фигура - разновидность силлогизма, в которой средний термин занимает место предиката в большей и место субъекта в меньшей посылке (Р - M, M - S), схематично выражается: Р - М - большая посылка. М - S - меньшая посылка. S - Р - заключение. Четвертая фигура силлогизма практически не употребляется. По первой фигуре можно получить выводы из всех основных видов суждений. Вторая фигура дает только отрицательный вывод. В третьей фигуре вывод будет частным суждением. 35. Умозаключение из сложных суждений (чисто-условное умозаключение). Чисто условными называется умозаключения, в которых обе посылки и заключение представляют собой условные высказывания, т.е. сложные высказывания, составленные из простых высказываний с помощью логического союза «если…, то…», Если изобретение создано совместным творческим трудом нескольких граждан (р), все они признаются соавторами изобретения (q). Если они признаются соавторами изобретения (r), то порядок пользования правами на изобретение, созданное в соавторстве, определяется соглашением между соавторами (r). Если изобретение создано совместным творческим трудом нескольких граждан (р), то порядок пользования правами на изобретение, созданное в соавторстве, определяется соглашением между соавторами (r). В приведенном примере обе посылки – условные суждения, причем следствие первой посылки является основанием второй (q), из которого, в свою очередь, вытекает некоторое следствие (r). Общая часть двух посылок (q) позволяет связать основание первой (р) и следствие второй (r). Поэтому заключение также выражается в форме условного суждения. Схема чисто условного умозаключения: (p → q) ∧ (q → r), (Р → r). Вывод в чисто условном умозаключении основывается на правиле: следствие следствия есть следствие основания. Умозаключение, в котором заключение получается из двух условных посылок, относится к простым. Однако заключение может следовать из большего числа посылок, которые образуют цепь условных суждений. Такие умозаключения называются сложными. 36. Умозаключение из сложных суждений (условно-категорическое умозаключение). Условно-категорическим называется умозаключение, в котором одна из посылок – условное, а другая посылка и заключение – категорические суждения. Это умозаключение имеет два правильных модуса: утверждающий и отрицающий. 1. В утверждающем модусе - посылка, выраженная категорическим суждением, утверждает истинность основания условной посылки, а заключение утверждает истинность следствия; рассуждение направлено от утверждения истинности основания к утверждению истинности следствия. Напр.: Если иск предъявлен недееспособным лицом (р), то суд оставляет иск без рассмотрения (q). Иск предъявлен недееспособным лицом (р). Суд оставляет иск без рассмотрения (q). Первая посылка – условное суждение, выражающее связь основания (р) и следствия (q). Вторая посылка – категорическое суждение, в котором утверждается истинность основания (р): иск предъявлен недееспособным лицом. Признав истинность основания (р), мы признаем истинность следствия (q): суд оставляет иск без рассмотрения. Утверждающий модус дает достоверные выводы. Он имеет схему: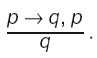 2. В отрицающем модусе (modus tollens) посылка, выраженная категорическим суждением, отрицает истинность следствия условной посылки, а заключение отрицает истинность основания. Рассуждение направлено от отрицания истинности следствия к отрицанию истинности основания. Напр.: Если иск предъявлен недееспособным лицом (р), то суд оставляет иск без рассмотрения (q). Суд не оставил иск без рассмотрения (? q). Неверно, что иск предъявлен недееспособным лицом (?р). Схема отрицающего модуса:

.Эти модусы подчиняются правилу: утверждение основания ведет к утверждению следствия и отрицание следствия – к отрицанию основания. Два других модуса достоверных заключений не дают. Они называются неправильными модусами и подчиняются правилу: отрицание основания не ведет с необходимостью к отрицанию следствия и утверждение следствия не ведет с необходимостью к утверждению основания.

37. Умозаключение из сложных суждений (разделительно-категорическое умозаключение). Разделительно-категорическим называется умозаключение, в котором одна из посылок – разделительное, а другая посылка и заключение – категорические суждения. Простые суждения, из которых состоит разделительное (дизъюнктивное) суждение, называются членами дизъюнкции, или дизъюнктами. Напр., разделительное суждение «Облигации могут быть предъявительскими или именными» состоит из двух суждений – дизъюнктов: «Облигации могут быть предъявительскими» и «Облигации могут быть именными», соединенных логическим союзом «или». Утверждая один член дизъюнкции, мы с необходимостью должны отрицать другой и, отрицая один из них, – утверждать другой. В соответствии с этим различают два модуса: утверждающе-отрицающий и отрицающе-утверждающий. 1. В утверждающе-отрицающем модусе - меньшая посылка, категорическое суждение, утверждает один член дизъюнкции, заключение – также категорическое суждение – отрицает другой ее член. Напр.: Облигации могут быть предъявительскими (р) или именными (q). Данная облигация предъявительская (p). Данная облигация не является именной (q). Схема утверждающе-отрицающего модуса:

 где – символ строгой дизъюнкции.

Заключение по этому модусу всегда достоверно, если соблюдается правило: большая посылка должна быть исключающе-разделительным суждением, или суждением строгой дизъюнкции. Если это правило не соблюдается, достоверного заключения получить нельзя. 2. В отрицающе-утверждающем модусе - меньшая посылка отрицает один дизъюнкт, заключение утверждает другой. Напр.: Облигации могут быть предъявительскими (р) или именными (q). Данная облигация не является предъявительской (?р). Данная облигация именная (q). Схема отрицающе-утверждающего модуса:

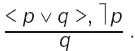
где < > – символ закрытой дизъюнкции. Утвердительный вывод получен посредством отрицания: отрицая один дизъюнкт, мы утверждаем другой. Заключение по этому модусу всегда достоверно, если соблюдается правило: в большей посылке должны быть перечислены все возможные суждения – дизъюнкты, иначе говоря, большая посылка должна быть полным (закрытым) дизъюнктивным высказыванием. Применяя неполное (открытое) дизъюнктивное высказывание, достоверного заключения получить нельзя.Разделительная посылка может включать не два, а три и больше членов дизъюнкции. 38. Умозаключение из сложных суждений (деструктивная дилемма (простая и сложная)). Дилеммами называются рассуждения, посылками которых являются по меньшей мере два условных высказывания (высказывания с «если, то») и одно разделительное высказывание (высказывание с «или»). Простая деструктивная дилемма - 1-я условная посылка указывает на то, что из одного и того же основания вытекают 2 различных следствия, 2-я посылка это отрицания обоих этих следствий, а в заключении отрицается основание. Простая деструктивная (отрицающая) дилемма: Если А, то В. Если А, то С. Неверно В или неверно С. Неверно А. Например: «Если число делится на 6, то оно делится на 3; если число делится на 6, то оно делится на 2; рассматриваемое число не делится на 2 или не делится на 3; следовательно, число не делится на 6». Сложная деструктивная дилемма - 1 посылка состоит из 2-х условных суждений с разными основаниями и разными следствиями, 2-я посылка - это отрицание обоих следствий Сложная деструктивная дилемма: Если А, то В. Если С, то Д. Не-В или не-Д. Не-А или не-С. Например: «Если поеду на север, то попаду в Тверь; если поеду на юг, то попаду в Тулу; но не буду в Твери или не буду в Туле; следовательно, не поеду на север или не поеду на юг». 39. Умозаключение из сложных суждений (конструктивная дилемма (простая и сложная)). Простая конструктивная дилемма - состоит из 2-х посылок. В 1-й утверждается, что из 2-х разных оснований вытекает одно следствие. Во 2-й утверждаются, что оба этих основания истинны. В заключении утверждается следствие. Простая конструктивная (утверждающая) дилемма: Если А, то С. Если В, то С. А или В. С Например: «Если прочту детектив Агаты Кристи, то хорошо проведу вечер; если прочту детектив Жоржа Сименона, тоже хорошо проведу вечер; прочту детектив Кристи или прочту детектив Сименона; значит, хорошо проведу вечер». Сложная конструктивная дилемма. Два основания в 1-й посылке, во 2-й посылке утверждается истинность одного или другого основания, в заключении утверждается истинность одного или другого следствия. Сложная конструктивная дилемма: Если А, то В. Если С, то Д. А или С. В или Д. Например: «Если будет дождь, мы пойдем в кино; если будет холодно, пойдем в театр; будет дождь или будет холодно; следовательно, мы пойдем в кино или пойдем в театр». 40. Понятие индуктивного умозаключения. Виды индукции. В индукции из нескольких частных случаев выводится общее правило, рассуждение идёт от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы, как правило, вероятностны.

Индукция бывает полной и неполной. В полной индукции перечисляются все объекты из какой-либо группы и делается вывод обо всей этой группе. Например, если в посылках индуктивного умозаключения перечисляются все девять крупных планет Солнечной системы, то такая индукция является полной: Меркурий движется. Венера движется. Земля движется. Марс движется… Плутон движется. Меркурий, Венера, Земля, Марс, … Плутон – это крупные планеты Солнечной системы. Все крупные планеты Солнечной системы движутся. В неполной индукции перечисляются некоторые объекты из какой-либо группы и делается вывод обо всей этой группе. Например, если в посылках индуктивного умозаключения перечисляются не все девять крупных планет Солнечной системы, а только три из них, то такая индукция является неполной: Меркурий движется. Венера движется. Земля движется. Меркурий, Венера, Земля – это крупные планеты Солнечной системы. Все крупные планеты Солнечной системы движутся. Понятно, что выводы полной индукции достоверны, а неполной – вероятностны, однако полная индукция встречается редко, и поэтому под индуктивными умозаключениями обычно подразумевается неполная индукция. 41. Полная индукция. Методы, правила. Полными называются умозаключения, в которых вывод делается на основе всестороннего изучения всей совокупности предметов определенного класса. Применяется полная индукция только в случаях, когда можно определить весь круг предметов, входящих в рассматриваемый класс, т. е. когда их число ограничено. Таким образом, полная индукция применяется лишь в отношении замкнутых классов. В этом смысле применение полной индукции не очень распространено. При этом такое умозаключение дает достоверное значение, так как все предметы, о которых делается заключение, перечислены в посылках. Вывод производится только относительно этих предметов. Для того чтобы можно было говорить о полной индукции, необходимо проверять соблюдение ее правил, условий. Так, первое правило гласит, что количество предметов, входящих в рассматриваемый класс, должно быть ограничено и определено; их количество не должно быть большим. Каждому элементу взятого класса, относительно которого создается умозаключение, должен быть присущ характерный признак. И наконец, выведение полного умозаключения должно быть обоснованным, необходимым, рациональным. Схему полного умозаключения можно отразить как: 51 – Р 52 – Р 53 – Р Sn – Р. Пример полного индуктивного умозаключения. Все обвинительные приговоры издаются в особом процессуальном порядке. Все оправдательные приговоры издаются в особом процессуальном порядке. Обвинительные приговоры и оправдательные приговоры есть решения суда. Все решения суда издаются в особом процессуальном порядке. В этом примере отражен класс предметов – решения суда. Все (оба) его элементы были указаны. Правая сторона каждой из посылок справедлива по отношению к левой. Поэтому общий вывод, который имеет непосредственное отношение к каждому падежу в отдельности, является объективным и истинным. 43. Неполная индукция (научная, популярная). Методы, правила.

Неполная индукция - такое умозаключение, в котором общий вывод делается на основании изучения некоторой части класса однородных предметов. Схема: S₁ суть Р S₂ суть Р S_n суть Р S₁ ... S_n - элементы класса Все S суть Р - этот вывод представляет собой вероятное(правдоподобное) знание. правила: 1. Необходимо подбирать как можно больше исходных посылок. Требуется проверить уровень успеваемости учащихся в некой школе. Предположим, что всего в ней учится 1 000 человек. По методу полной индукции надо протестировать на предмет успеваемости каждого ученика из этой тысячи. Поскольку сделать это довольно сложно, можно использовать метод неполной индукции: протестировать какую-то часть учащихся и сделать общий вывод об уровне успеваемости в данной школе. Различные социологические опросы также базируются на применении неполной индукции. Очевидно, что чем большее число учеников подвергнется тестированию, тем более надёжной будет база для индуктивного обобщения, и более точным получится вывод. Однако просто большего числа исходных посылок, как того требует рассматриваемое правило, для повышения степени вероятности индуктивного обобщения недостаточно. Допустим, тестирование пройдёт немалое число учащихся, но, волей случая, среди них окажутся одни только неуспевающие. В этой ситуации мы придём к ложному индуктивному выводу о том, что уровень успеваемости в данной школе очень низок. Поэтому первое правило дополняется вторым. 2. Необходимо подбирать разнообразные посылки. Возвращаясь к нашему примеру, отметим, что множество тестируемых должно быть не просто по возможности большим, но и специально, по системе, сформированным, а не случайно подобранным, т. е. надо позаботиться о том, чтобы в него вошли учащиеся (примерно в одинаковом количественном отношении) из разных классов, параллелей и т. п. И, наконец, третье правило неполной индукции предписывает следующее. 3. Необходимо делать вывод только на основе существенных признаков. Если, допустим, во время тестирования выясняется, что ученик 10 класса не знает наизусть всю периодическую систему химических элементов, то этот факт (признак) является несущественным для вывода о его успеваемости. Однако, если тестирование показывает, что ученик 10 класса частицу «не» с глаголом пишет слитно, то этот факт (признак) следует признать существенным (важным) для вывода об уровне его образованности и успеваемости. Первая ошибка, часто встречающаяся в неполной индукции, называется поспешным обобщением. Скорее всего, каждый из нас, хорошо с ней знаком. Всем приходилось слышать такие высказывания: «Все мужчины чёрствые», «Все женщины легкомысленные».. Например: К. учится плохо. Н. учится плохо. С. учится плохо. К., Н., С. – это ученики 10 «А». Все ученики 10 «А» учатся плохо. Неудивительно, что поспешное обобщение лежит в основе многих голословных утверждений, слухов и сплетен. Вторая ошибка носит длинное и, на первый взгляд, странное название: после этого, значит по причине этого. В данном случае речь идёт о том, что если одно событие происходит после другого, то это не означает с необходимостью их причинно-следственную связь. Два события могут быть связаны всего лишь временной последовательностью (одно – раньше, другое – позже). Например: Позавчера двоечнику Н. перебежала дорогу чёрная кошка, и он получил двойку. Вчера двоечнику Н. перебежала дорогу чёрная кошка, и его родителей вызвали в школу. Сегодня двоечнику Н. перебежала дорогу чёрная кошка, и его исключили из школы. Во всех несчастьях двоечника Н. виновата чёрная кошка. Из-за ошибки «после этого, значит по причине этого» рождаются небылицы, суеверия и мистификации. Третья ошибка, широко распространённая в неполной индукции, называется подмена условного безусловным. Рассмотрим индуктивное умозаключение, в котором из истинных посылок вытекает ложный вывод: Дома вода кипит при температуре 100 °C. На улице вода кипит при температуре 100 °C. В лаборатории вода кипит при температуре 100 °C. Вода везде кипит при температуре 100 °C. Мы знаем, что высоко в горах вода кипит при более низкой температуре. То, что проявляется в одних условиях, может не проявляться в других. В посылках рассмотренного примера присутствует условное (происходящее в определённых условиях), которое подменяется безусловным (происходящим во всех условиях одинаково, не зависящим от них) в выводе. Неполная индукция бывает популярной и научной. В популярной индукции вывод делается на основе наблюдения и простого перечисления фактов, без знания их причины, а в научной индукции вывод делается не только на основе наблюдения и перечисления фактов, но ещё и на основе знания их причины. Поэтому научная индукция, в отличие от популярной, характеризуется намного более точными, почти достоверными выводами. Главное отличие научной индукции от популярной заключается в знании причин происходящих событий. Поэтому одна из важных задач не только научного, но и повседневного мышления – это обнаружение причинных связей и зависимостей в окружающем нас мире. 43. Умозаключения по аналогии. Методы, правила. Умозаключение по аналогии – это вывод о принадлежности определенного признака исследуемому единичному объекту (предмету, событию, отношению или классу) на основе его сходства в существенных чертах с другим уже известным единичным объектом. Логический переход от известного к новому знанию регулируется в выводах по аналогии следующим правилом: если два единичных предмета сходны в определенных признаках, то они могут быть сходны и в других, обнаруженных в одном из сравниваемых предметов, признаках. Первое условие для аналогии — тщательное выявление сходных признаков сравниваемых предметов. Причем эти признаки должны быть не второстепенными, а существенными. Чем больше сходных признаков и чем они существеннее, тем больше оснований предполагать, что вывод по аналогии истинен. Второе условие — выяснение различий сравниваемых предметов, т. е. какие признаки отличают их друг от друга, и существенности этих признаков. Чем меньше таких признаков, тем ближе к истине вывод по аналогии. Третье условие — тщательное исследование как объективной взаимосвязи и взаимозависимости сходных признаков, так и связи этих сходных признаков с тем, который мы переносим на исследуемый предмет. Метод аналогии дает наиболее ценные результаты тогда, когда устанавливается органическая взаимосвязь не только сходных признаков, но и связь с тем признаком, который переносится на исследуемый предмет, объект. В зависимости от характера информации, переносимой с одного предмета на другой (с модели на прототип), аналогия делится на два вида: аналогия свойств и аналогия отношений. В аналогии свойств рассматриваются два единичных предмета (или два множества однородных предметов, два класса), а переносимыми признаками являются свойства этих предметов. Схема аналогии свойств в традиционной логике такова:

Предмет А обладает свойствами а, b, с, d, e,f. Предмет В обладает свойствами а, b, с, d. ___________________________________________ Вероятно, предмет В обладает свойствами е, f. Примером аналогии свойств может служить аналогия симптомов протекания той или иной болезни у двух разных людей (два единичных предмета) или у двух групп людей (например, взрослых и детей). Исходя из сходства признаков болезни (симптомов), врач ставит диагноз. В аналогии отношений информация, переносимая с модели на прототип, характеризует отношения между двумя предметами. Пусть имеется отношение (aRb) и отношение (mR₁n).Сходными, аналогичными выступают отношения R и R₁, но а не аналогично m, а b не аналогично n. Примером является предложенная Резерфордом планетарная модель строения атома, которую он построил на основании аналогии отношения между Солнцем и планетами, с одной стороны, и ядром атома и электронами, которые удерживаются на своих орбитах силами притяжения ядра, — с другой. Здесь R — взаимодействие противоположно направленных сил — сил притяжения и отталкивания — между планетами и Солнцем, а R₁— взаимодействие противоположно направленных сил — сил притяжения и отталкивания — между ядром атома и электронами. 44. Доказательство. Структура, виды. Доказательство - логическая форма мысли, обосновывающая истинность положения через другие положения,истинность которых уже обоснована или очевидна. В составе доказательства (и опровержения) выделяются: тезис доказательства, аргументы, промежуточные допущения и форма доказательства. Тезис доказательства - высказывание, истинность или ложность которого доказывается. Аргументы - высказывания, посредством которых осуществляется доказательство тезиса. В доказательстве аргументы обязательно должны быть истинными. Промежуточные допущения - вспомогательные допущения, которые вводятся в процессе рассуждения (дедукции) и устраняются затем при переходе к окончательному результату рассуждения. Эти высказывания могут быть как истинными, так и ложными. Например, в так называемых доказательствах «от противного» в качестве промежуточных допущений вводятся заведомо ложные высказывания. Форма доказательства - логический способ обоснования тезиса при помощи аргументов (возможно, с использованием промежуточных допущений). Основными видами доказательств, различающихся по форме, являются доказательства прямые и непрямые (косвенные). Прямое доказательство - это дедуктивный вывод, в котором тезис (Т) непосредственно выводится из аргументов (А) в качестве заключения вывода. Другими словами, истинность тезиса выводится из истинности аргументов без введения дополнительных предположений. Пример. Все млекопитающие дышат легкими. Кит – млекопитающее. Из этого следует, что и кит дышит легкими. Непрямое (косвенное) доказательство истинности или ложности некоторого тезиса (Т) состоит в том, что оно достигается посредством опровержения некоторых других высказываний, несовместимых с тезисом. Косвенное доказательство, в свою очередь, подразделяется на два вида: доказательство «от противного» и разделительное. Пример. Если бы Теплов совершил убийство, то он был бы на месте преступления в ту ночь, когда оно было совершено. Но в ту ночь Теплов не был на месте преступления, что подтверждено свидетельскими показаниями. Следовательно, он не совершал данного убийства. Доказательство посредством исключения альтернатив (разделительное) по формальной структуре совпадает с разделительно-категорическим умозаключением, имеющим отрицающе-утверждающий модус, и является обобщением формы этого умозаключения: Пример. Мы предполагаем, что какой-то поступок был совершен либо Майоровым, либо Корнеевым, либо Гладких. Но на основании имеющихся аргументов вынуждены признать, что ни Майоров, ни Корнеев не совершали этого поступка. Исключая соответствующие альтернативы дизъюнкции, получаем заключение: «Поступок совершил Гладких». 45. Прямое доказательство. Правила, схемы. Прямое доказательство - это дедуктивный вывод, в котором тезис (Т) непосредственно выводится из аргументов (А) в качестве заключения вывода. Другими словами, истинность тезиса выводится из истинности аргументов без введения дополнительных предположений. Пример. Все млекопитающие дышат легкими. Кит – млекопитающее. Из этого следует, что и кит дышит легкими. Прямым называют доказательства, в котором истинность тезиса обосновывается, исходя непосредственно из аргументов Правила по отношению к тезису. - Необходимо в большинстве случаев сформулировать тезис четко и ясно (в виде суждения, системы суждений, проблемы, гипотезы, концепции). Это особенно важно в споре, спорная мысль не должна оставаться неясной. - Тезис должен быть истинным. (Как ни пытались доказать возможность создания и существования вечного двигателя, никому этого не удалось). - Тезис не должен изменяться в процессе аргументации без специальных оговорок. Правила по отношению к аргументам. - Аргументы должны быть сформулированы четко и ясно. - Аргументы должны быть суждениями полностью или хотя бы частично обоснованными. - Аргументы должны повышать правдоподобие тезиса в доказательстве и снижать его в опровержении тезиса оппонента. Существует также общее правило по отношению к демонстрации. Отношение между аргументами и тезисом должно быть отношением логического следования или по меньшей мере – отношением подтверждения. Схема прямого доказательства:

1. Подбираются аргументы, прямо направленные на обоснование тезиса (по дедукции, по индукции или аналогии).

Пример 1: Доказать тезис: Все студенты группы 555 – успевающие студенты. Решение: А) Прямое дедуктивное доказательство: Студенты, вовремя и успешно сдающие экзамены, являются успевающими студентами. Все студенты группы 555 вовремя и успешно сдают экзамены. Значит, действительно, все студенты группы 555 – успевающие студенты. Здесь в качестве демонстрации применялся простой категорический силлогизм, построенный по первой фигуре: Правила ПКС соблюдены. Значит, умозаключение построено правильно. Тезис доказан. Б) Прямое доказательство по индукции: Студент А – успевающий студент. Студент Б – успевающий студент. … Студент Я – успевающий студент. Студенты А, Б, .. Я – все студенты 555 группы.

Значит, все студенты 555 группы – успевающие студенты. 46. Косвенное доказательство. Апагогическое доказательство. Правила, схемы. Косвенное доказательство - такое доказательство, в котором тезис не выводится прямо из аргументов, а обосновывается с помощью конкурирующих с тезисом допущений. Различают два вида косвенных доказательств: косвенное апагогическое доказательство и косвенное разделительное доказательство. Косвенное апагогическое доказательство - это обоснование истинности тезиса путем установления ложности антитезиса (антитезисом называется суждение, противоречащее тезису). К косвенному апагогическому доказательству прибегают в тех случаях, когда выдвинутый тезис(Т) невозможно доказать прямо, непосредственно. Например, требуется доказать тезис «Н. не совершал данного убийства» (Т). Аргументов, из которых можно было прямо вывести данный тезис, у следователя нет. Тогда он допускает истинным антитезис ( Т): «Н. совершил данное убийство». Из данного антитезиса выводятся следствия, в числе которых может быть и такое: «Н. должен был находиться в момент совершения преступления на месте преступления» (С₁). Но у следствия имеются доказанные сведения о том, что в ночь, когда было совершено данное преступление, Н. находился в другом городе и, следовательно, не мог находиться на месте преступления в момент его совершения. Отсюда следует: «Если Н. совершил данное убийство, то Н. должен был находиться в момент совершения преступления на месте преступления ( Т →С₁). Ложно, что Н. находился в момент совершения преступления на месте преступления (С₁). Следовательно, ложно, что Н. совершил данное убийство (ложно, что Т). Но если ложен антитезис, то истинно его отрицание (ТилиТ). В данном случае доказательство построено по отрицающему модусу условно-категорического умозаключения. Косвенное апагогическое доказательство тезиса можно изобразить на схеме.

3. Следствия сопоставляются с фактами, отрицаются некоторые следствия С₁, С₂, С₃. 4. Строится умозаключение (по форме отрицающего модуса условнокатегорического умозаключения).

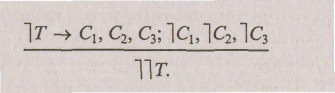
5. В заключении на основании закона двойного отрицания можно утверждать истинность тезиса Т. Символически:

В) Косвенное апагогическое доказательство:

1. Условно выдвигаем антитезис: Если бы не все студенты группы 555 были успевающими.

2. Выводим следствия. Тогда бы среди них были задолжники по сессии.

3. Опровергаем следствия. Но среди них нет задолжников по сессии.

4. Значит, наше допущение «не все студенты группы 555 – успевающие студенты» ложно. Следовательно, истинно, что все студенты группы 555 – успевающие студенты.

47. Косвенное доказательство. Разделительное доказательство. Правила, схемы. Доказательство посредством исключения альтернатив (разделительное) по формальной структуре совпадает с разделительно-категорическим умозаключением, имеющим отрицающе-утверждающий модус, и является обобщением формы этого умозаключения: Например, нужно доказать, что одна величина равна другой. Ясно, что возможны только три варианта: или две величины равны, или первая больше второй, или, наконец, вторая больше первой. Если удалось показать, что ни одна из величин не превосходит другую, два варианта будут отброшены и останется только третий: величины равны. Оно применяется в тех случаях, когда известно, что доказываемый тезис входит в число альтернатив, полностью исчерпывающих все возможные альтернативы данной области. Доказательство идет по простой схеме: одна за другой исключаются все возможности, кроме одной, которая и является доказываемым тезисом. 48. Правила (возможные ошибки из нарушений правил) для тезиса, аргументов, демонстрации (логического следования). 1. Тезис должен быть сформулирован ясно и точно. Ошибки, возникающие при нарушении этого правила, могут состоять в том, что тезис сформулирован нечетко, не определяет точно, что подлежит обоснованию, или допускает различные истолкования. Пример. Так, тезис «Капитализм лучше социализма» является неясным, потому что одно может быть хуже или лучше другого в экономическом, социально-политическом, духовном и прочих отношениях. 2. Тезис должен оставаться постоянным на протяжении всего доказательства. Он не должен меняться, по крайней мере, без специальных оговорок. Ошибки, возникающие в результате нарушения этого правила: 1) «Подмена тезиса» – логическая ошибка, состоящая в замене тезиса на другое похожее суждение, которое легче поддаётся доказательству и доказательство которого выдаётся за доказательство первоначального тезиса. Пример. Предположим, в суде доказывается виновность определенного человека в совершении преступления. Однако прокурор доказывает факт совершения обвиняемым данного преступления. Но юридически виновность в совершении некоторого действия состоит не в самом факте его осуществления, а включает также ряд моментов социально-психологического характера: способность или неспособность предвидения последствий поступка, наличие или отсутствие намерений вызвать эти последствия и т.д. 2) «Потеря тезиса» - ошибка, аналогичная первой, но совершаемая непреднамеренно. Правила для аргументов 1. Аргументы должны быть истинными суждениями. 2. Аргументы должны быть доказаны и являться достаточным основанием для признания истинности тезиса. 3. Истинность аргументов должна обосновываться независимо от тезиса. 4. Аргументы не должны противоречить друг другу. Ошибки по отношению к аргументам. 1. Ложность аргумента. Использование в доказательстве ложного аргумента приводит к необоснованности доказываемого тезиса. Эта ошибка имеет несколько разновидностей. Одна из них - так называемый «дамский аргумент». Пример. Человек возмущается, что при починке его ботинок сделали очень высокие каблуки. Мастер отвечает: «Что же Вы, предпочитаете совсем без каблуков ходить?» Или вы упрекаете знакомого в том, что он ответил кому-то довольно грубо. Знакомый возражает: «Что ж, по-вашему, я лебезить перед ним должен?» В этих рассуждениях, по существу, используются ложные дизъюнкции «А или В», где А и В – противоположности (крайности), между которыми на самом деле есть промежуточные возможности, но рассуждающий склонен считать, что таких возможностей нет. К числу ошибок, связанных с ложными аргументами, относится ошибка «слишком много доказывается». В этом случае ложность аргумента сама по себе не так очевидна, однако обнаруживается, что из него следует не только тезис, но и какое-нибудь ложное положение. Пример. Во время дискуссий о необходимости запрещения пропаганды войны некоторые их участники выдвигали тезис о том, что нельзя запрещать пропаганду войны, поскольку это означало бы ограничение демократического принципа свободы слова. Возражения по поводу этого аргумента были следующими: «При таком понимании свободы слова (как абсолютной свободы) не следовало бы запрещать также призывы к убийствам, террористическим актам, диверсиям и т.д.». Однако такого рода запреты имеются даже в самых демократических государствах. И значит, выдвигаемый аргумент является ложным. 2. «Предвосхищение основания». Эта ошибка заключается в том, что в качестве оснований используются положения, истинность которых еще не доказана. Пример. Если доказывают тезис «Все студенты стремятся к знаниям» и в качестве аргумента приводят суждение «Все люди стремятся к знаниям», то совершается ошибка «предвосхищение основания», поскольку само суждение, приводимое в качестве аргумента, нуждается в обосновании. 3. «Слишком мало доказывается». Ошибка встречается тогда, когда тезис остаётся частично недоказанным или аргументы не являются достаточным основанием для признания истинности тезиса. Пример. Предположим, мы хотим доказать, что господин Белоусов добродетелен. Если бы мы при этом доказали, что о нем не известно ничего дурного, и на этом основании стали бы настаивать на истинности нашего тезиса, то мы совершили бы ошибку «слишком мало доказывается». 4. «Круг в доказательстве». Ошибка состоит в том, что тезис обосновывается с помощью аргумента, истинность которого требует обоснования с помощью самого тезиса. Пример 1. Ученик утверждает, что число 106 является натуральным (тезис). Аргументы: «Оно является членом натурального ряда, а всякий член натурального ряда есть натуральное число». Но на вопрос о том, откуда видно, что оно является членом натурального ряда, следует ответ: «Это ясно из того, что число это является натуральным!» Ошибка «круг в доказательстве» может возникать, если в качестве аргумента в доказательстве используется утверждение, обоснование которого неявно предполагает уже истинность тезиса. Такой аргумент представляет собой либо некоторую замаскированную переформулировку тезиса, либо, будучи сложным высказыванием, содержит тезис в качестве своей составной части. Пример 2. Некоторые философы доказывали, что мир имел начало во времени, аргументируя так: «Если бы мир не имел начало во времени, то это означало бы, что к настоящему времени была бы отсчитана бесконечность. Но бесконечность нельзя отсчитать. Следовательно, мир имел начало во времени». В аргументе «В случае бесконечности мира во времени была бы отсчитана бесконечность» содержится как раз утверждение о том, что мир имел начало во времени. Ибо само понятие «отсчитано» указывает на то, что имеется начало и конец отсчета. Очевидно, что в таких случаях, так же как и в случае «круга в доказательстве», имеет место ошибка, состоящая в необоснованности аргумента. 5. Противоречие в аргументах. Ошибка заключается в том, что аргументы оказываются противоречащими друг другу суждениями. Пример. Обвиняемый в своих интересах воспользовался подложной телеграммой об открытии наследства. На процессе он утверждал, что искренне верил этой телеграмме. Защита выставила для подтверждения слов обвиняемого двух свидетелей. Первый свидетель сказал, что обвиняемый крайне расстроился, узнав о подделке. Второй свидетель, который был у него позже, показал, что он стал очевидцем обморока, когда обвиняемый узнал о подделке. Однако присяжные решили, что один и тот же человек не мог быть поражен одним и тем же событием два раза. ПРАВИЛА И ОШИБКИ В ХОДЕ ДЕМОНСТРАЦИИ Логическая связь аргументов с тезисом протекает в форме таких умозаключений, как дедукция, индукция и аналогия. Логическая корректность демонстрации зависит от соблюдения правил соответствующих умозаключений. 1) Дедуктивный способ аргументации предполагает соблюдение ряда методологических и логических требований. К важнейшим из них относятся следующие. (1) Точное определение или описание в большей посылке, выполняющей роль довода, исходного теоретического или эмпирического положения. Это дает возможность убедительно продемонстрировать научные позиции или практические соображения, которыми руководствуются при оценке конкретного события.              (2) Точное и достоверное описание конкретного события, которое дано в меньшей посылке. Это требование диктуется методологическим принципом конкретности истины. В противном случае дедуктивное рассуждение будет двусмысленным и далеким от истины. Точное описание события или явления помогает отыскать среди теоретических положений нужное обобщение и правильно применить его к конкретному случаю. Несоблюдение этого правила нередко приводит к тому, что лишь приблизительно, «на глазок» выбирают соответствующее общее положение или явно ошибочную оценку конкретному событию. Наиболее опасной ошибкой такого рода является догматическое применение верного для сугубо конкретной ситуации положения как безусловного и действующего при любых условиях. (3) Дедуктивная аргументация приводит к достоверному обоснованию тезиса при соблюдении структурных правил этой формы вывода, относящихся к терминам, количеству, качеству и логическим связям между посылками умозаключения. Это прежде всего правила категорических, условных, разделительных и смешанных форм силлогизмов, которые изложены в главе о дедуктивных умозаключениях. 2) Индуктивный способ аргументации применяется, как правило, в тех случаях, когда в качестве доводов используются фактические данные. Доказательное значение индуктивного обоснования зависит от устойчивой повторяемости свойств у однородных явлений. Чем больше число благоприятных случаев наблюдается и чем разнообразнее условия их отбора, тем основательнее индуктивная аргументация. Чаще всего индуктивное обоснование приводит лишь к проблематичным заключениям, ибо свойственное отдельным объектам не всегда присуще всей группе явлений. Индуктивное рассуждение приобретает логическую основательность, если оно сопровождается тщательным анализом событий и обнаруживает в разнообразных и случайных фактах проявление существенного и закономерного. В этом случае меняется логическая функция сведений о фактах: с одной стороны, они выступают в роли убедительных доводов, а с другой — служат наглядной иллюстрацией основной идеи. Индуктивное рассуждение, в котором не ограничиваются перечислением, а поднимаются до уровня существенного обобщения, ценно тем, что именно на этом пути происходит объяснение индукции и дедукции. Рациональное объединение индуктивного и дедуктивного способов обоснования является наиболее действенным методом аргументации. Его убеждающая сила состоит в том, что здесь ссылаются на конкретные примеры и факты реальной жизни в сочетании с дедуктивным рассуждением, в котором используются эмпирические обобщения и законы науки. 3) Аргументация в форме аналогии применяется в случае уподобления единичных событий и явлений. При обращений к аналогии надо соблюдать следующие правила этого вида умозаключения.

Во-первых, аналогия состоятельна лишь тогда, когда два явления сходны между собой не в любых, а лишь в существенных признаках. Во-вторых, при уподоблении двух явлений или событий следует учитывать различия между ними.Если два явления существенно отличаются друг от друга, то, несмотря на наличие сходных признаков, их нельзя уподоблять. Аналогия в этом случае будет несостоятельной. Поскольку аналогия общественно-исторических явлений не всегда дает безусловные и окончательные заключения, отсюда следует, что ею можно пользоваться лишь в качестве дополнения к дедуктивному или индуктивному обоснованию. Ошибки в демонстрации связаны с отсутствием логической связи между аргументами, и тезисом. В публичных выступлениях бывают случаи, когда для обоснования своей мысли оратор цитирует источники, приводит факты, ссылается на авторитетные мнения. Создается впечатление, что его речь достаточно аргументирования. Но при ближайшем рассмотрении оказывается, что концы с концами в рассуждении оратора не сходятся. Исходные положения — аргументы— логически «не склеиваются» с тезисом. В общем виде отсутствие логической связи между аргументами и тезисом называют ошибкой«мнимого следования». Мнимое следование часто возникает по причине несоответствия между логическим статусом посылок, в которых представлены аргументы, и логическим статусом суждения, содержащего тезис. Укажем на типичные случаи нарушения демонстрации безотносительно к видам употребляемых умозаключений. 1) Логический переход от узкой области к более широкой области. В аргументах, например, описывают свойства определенного вида явлений, а в тезисе неосновательно говорится о свойствах всего рода явлений, хотя известно, что не все признаки вида являются родовыми. 2) Переход от сказанного с условием к сказанному безусловно. Оратор выставляет аргументы, которые считаются истинными при известных условиях, т.е. выражает их в форме условных суждений. Например, В признается истинным, если будет установлена истинность А. В процессе же аргументации об этой условности забывают и приходят к выводу, что принятые аргументы с необходимостью обосновывают тезис, который формулируется в безусловной форме. В принципе же условные аргументы могут с необходимостью обосновывать лишь условно принимаемый тезис. (3) Переход от сказанного в определенном отношении к сказанному безотносительно к чему бы то ни было. Так, мнимым будет следование в том случае, если, опираясь на проблематичные, пусть даже весьма вероятные доводы, пытаются обосновать достоверный тезис. В общем виде несоответствие между аргументами и тезисом в случае мнимого следования проявляется в том, что логически слабыми аргументами (узкими, условными, относительными или проблематичными) пытаются обосновать логически более сильный тезис (широкий, безусловный, безотносительный или достоверный). 49. Доказательство и аргументация (логические характеристики сходства и различия) Под доказательством понимается процедура установления истинности некоторого утверждения путем приведения других утверждений, истинность которых уже известна и из которых с необходимостью вытекает первое. Доказательство связано с аргументацией, но они не тождественны. Аргументация - способ рассуждения, включающий доказательство и опровержение, в процессе которого создается убеждение в истинности тезиса и ложности антитезиса как у самого доказывающего, так и оппонентов; обосновывается целесообразное принятия тезиса с целью выработки активной жизненной позиции реализации определенных программ действий, вытекающих из доказываемого положения.

Понятие “аргументация” богаче по содержанию, чем понятие “доказательство”: целью доказательства является установление истинности тезиса, а целью аргументации еще и обоснование целесообразности принятия этого тезиса, пою его важного значения в данной жизненной ситуации и т. п.

В теории аргументации “аргумент” также понимается шире, чем в теории доказательства, ибо в первой имеются в виду не только аргументы, подтверждающие истинность тезиса, но и аргументы, обосновывающие целесообразность его принятия, демонстрирующие его преимущества по сравнению с другими подобными утверждениями (предложениями). Аргументы в процессе аргументации гораздо разнообразнее, чем в процессе доказательства.

50. Логические основы теории аргументации: доказательство, его логическая структура. Виды доказательства. Правила доказательства. доказательство– это логическая операция, состоящая в установлении истинности некоторого суждения посредством выведения его из других суждений, истинность которых установлена до этой операции и независимо от нее. Как логическая операция доказательство включает три составляющих элемента:

• тезис (суждение, истинность которого надо доказать или опровергнуть);

• аргументы (доводы, основания);

• демонстрация (способ доказательства).

В структуре доказательства тезис – главное. Его основная характеристика —• истинность. Ложный тезис доказать нельзя. Всякий тезис нуждается в доказательстве, представляющем собой выведенное знание из имеющегося знания. Тезис (греч. – утверждение, положение) – это то суждение, истинность или ложность которого обосновывается. В качестве тезиса могут выступать общие положения (обобщения) или высказывания о конкретных фактах. Тезисом, например, является закономерность, что полный и достоверный учет затрат обеспечивает достоверное исчисление показателя себестоимости продукции. Аргументы (доводы, основания) – исходные теоретические положения или фактические данные, истинность которых доказана ранее. Это суждения, истинность которых или уже установлена, или, по крайней мере, предполагается несомненной. В качестве аргументов могут выступать:

• ранее доказанные положения и научные обобщения;

• суждения об удостоверенных фактах;

• определения;

• аксиомы и др.

В систему аргументов входят:

• утверждения о фактах;

• определение понятий;

• аксиомы.

Особую доказательную силу имеют факты. Но они только тогда становятся аргументом (доводом) доказательства, если берутся не изолированно, а в их взаимной связи, как системы. Факт в качестве аргумента действенен в ситуациях, когда тезисом является единичное или частное суждение. Демонстрация представляет собой связь между тезисом и аргументами. Она протекает в форме умозаключений. Это могут быть отдельные умозаключения, но чаще – цепочка рассуждений, обосновывающих или отвергающих тезис. По способу аргументации все доказательства делятся на два вида: а) прямые и б) косвенные. Прямое доказательство заключается в непосредственном выведении из основания по определенным правилам умозаключения истинности или ложности данного тезиса. Косвенное доказательство заключается в обосновании ложности или истинности положения, находящегося в определенном отношении с тезисом, и отсюда опосредованно устанавливается истинность тезиса или, наоборот, его ложность. В процессе доказательства необходимо соблюдение определенных правил: 1. Тезис доказательства следует формулировать ясно и четко, не допуская двусмысленности его толкования. При этом необходимо убедиться в том, все ли слова и выражения тезиса вполне и отчетливо нам понятны, уяснить точный смысл терминов. 2. В ходе доказательства тезис должен оставаться неизменным (т.е. на протяжении всего доказательства). 3. Тезис и аргументы (доводы) должны быть ясными, точно определенными. 4. Тезис должен оставаться тождественным. 5. Тезис не должен содержать в себе логического противоречия. 6. Тезис не должен противоречить ранее высказанным суждениям. 7. Аргументы (доводы) не должны противоречить друг другу. 8. Аргументы (доводы) должны быть полными. 9. Аргументы (доводы) должны быть достаточными для тезиса. 10. Аргументы (доводы) должны быть истинными (доказанными). 11. Истинность аргументов (доводов) должна быть независима от тезиса (автономность аргументов). 12. Тезис и аргументы (доводы) должны быть, в конечном счете, обоснованы фактами. 13. Тезис и аргументы (доводы) не должны содержать в себе логические противоречия (быть непротиворечивыми). 14. Тезисы должны логически следовать из аргументов (доводов). 51.Логические основы теории аргументации: опровержение, его логическая структура. Основные способы опровержения. Опровержение – это логическая операция по установлению ложности тезиса. Задача опровержения – установить ложность выдвинутого положения или его недоказанность. Доказать тезис А – значит обосновать его истинность, а опровергнуть тезис А – значит обосновать его ложность. Например, существовало утверждение: «Нельзя переплыть на плоту через Тихий океан». Норвежский ученый Тур Хейердал опроверг это утверждение, переплыв со своими спутниками Тихий океан на плоту. Структура опровержения Тезис – положение, высказывание, которые необходимо опровергнуть. Аргументы – положения, истинные суждения, при помощи которых опровергается тезис. Аргументы выступают основанием опровержения. Форма опровержения или демонстрация – логический способ связи аргументов и тезиса опровержения. Существует три основные формы опровержения: критика тезиса, критика аргументов, критика демонстрации. 1. Критика тезиса имеет своей целью показ, что тезис несостоятелен. Это может быть сделано различными способами. Может быть показано, что тезис противоречив. Другой способ, продемонстрировать, что суждение, противоположное тезису, истинно и следовательно, об истинности тезиса рассуждать беспочвенно. Возможно показать, что следствия из тезиса ведут к противоречию. Критика тезиса и доказательство его ложности является самым главным способом опровержения. Но это есть и самый трудный путь опровержения. 2. Критика аргументов имеет своей целью показать несостоятельность аргументов. Это может быть показано путем демонстрации ложности аргументов, их противоречивости. Если в качестве аргументов используются факты, то может быть показана их недоказанность, недостоверность или противоречивость. Опровержение аргументов демонстрирует, что данной системы аргументов недостаточно для доказательства тезиса. Однако это не дискредитирует сам тезис, в данном случае достигается эффект демонстрации необоснованности тезиса. Бывают случаи, когда этого оказывается достаточно. В судебной практике, например, этого достаточно для того, чтобы показать недоказанность обвинения и, в силу презумпции невиновности, подозреваемый признается невиновным. 3. Критика демонстрации имеет своей целью показать, что использованные умозаключения содержат ошибки, что из данных аргументов не следует данный тезис. Наиболее распространенный прием опровержения – выведение из опровергаемого утверждения следствий, противоречащих истине. Хорошо известно, что, если даже одно-единственное логическое следствие некоторого положения неверно, ошибочным будет и само это положение. Уже на первых уроках физики в школе показывается опыт, придуманный когда-то итальянским физиком Э. Торричелли. Стеклянную трубку, запаянную с одного конца, наполняют ртутью и опрокидывают в чашку с ртутью. Ртуть из трубки не выливается, она только опускается немного, и над нею образуется вакуум, "торричеллиева пустота". Ртуть в трубке на определенном уровне поддерживает давление атмосферы. "Опыты с несомненностью доказывают, – заявлял Э. Торричелли, – что воздух имеет вес..." Если кто-либо утверждает, что воздух невесом, можно сослаться на этот опыт. Если бы воздух не имел веса, он не давил бы на ртуть в чашке и уровень ртути в трубке сравнялся бы с уровнем в чашке. Но этого не происходит; значит, неверно, что у воздуха нет веса. Другой прием установления несостоятельности выдвигаемого кем-либо положения – доказательство справедливости отрицания этого положения. Утверждение и его отрицание не могут быть одновременно истинными. Как только удается показать, что верно отрицание рассматриваемого положения, вопрос об истинности самого этого положения автоматически отпадает. Достаточно, скажем, показать одного черного лебедя, чтобы опровергнуть убеждение в том, что лебеди бывают только белыми. 52. Формы организации информативного общения: диалог, полемика, спор, дискуссия, выступление. Виды диалога и их цели. Диалог – это логико-коммуникативный процесс, где субъекты (разных уровней) вступают во взаимодействие посредством смысловых позиций для решения определённых задач. Спор является древнейшей формой диалога, в ходе которого каждая из сторон стремится убедить другую в обоснованности и истинности своей позиции, точки зрения или мнения по обсуждаемому вопросу, когда не существует единого мнения по его решению. Спор состоит из доказательств. Один доказывает, что такая-то мысль верна, другой – что она ошибочна. Та мысль, для обоснования истины или ложности которой строится доказательство, называется тезисом доказательства. Вокруг нее должно вращаться все доказательство. Она – конечная цель наших усилий. Дискуссия – это разновидность публичного спора. Целью дискуссии является выяснение и сопоставление различных точек зрения на заданную проблему, выявление истины и нахождение решения. Дискуссия представляет собой эффективный способ убеждения оппонента. Разновидностью дискуссии является диспут – спор на научную или публицистическую тему. По своему логическому характеру дискуссия является наиболее организованной и систематической формой диалога, ориентированного на поиск истины. Хотя в таком поиске используются и доказательные рассуждения, когда речь идет, например, о применении ранее доказанных истин (принципов, законов и теорий), но доминирующая роль в нем принадлежит аргументации, опирающейся на правдоподобные (или вероятностные) рассуждения. Полемика отличается от дискуссии тем, что в ней сторонники противоположных взглядов не ставят своей целью достижение компромисса. Наоборот, главные усилия противоборствующих сторон направлены на то, чтобы утвердить свою позицию по спорному вопросу и опровергнуть взгляды противника. Такая характеристика согласуется со смыслом самого термина "полемика", означающего в переводе с греческого воинственный, враждебный спор. Полемика большей частью проводится по вопросам, которые в какой-то мере уже исследованы, но тем не менее по ним существуют разногласия. Каждая из сторон использует полемику для защиты своих взглядов, мнений и решений, опираясь на то, что уже достигнуто в понимании и обосновании спорных вопросов. ЛОГИКА ПУБЛИЧНОГО ВЫСТУПЛЕНИЯ - предполагает наличие четкой структуры речи, последовательности и объективной обоснованности выдвигаемых положений, богатство аргументации.  

Виды диалога: 1. Обычный диалог (беседа на определенную тему). 2. Дискуссия (обмен мнениями). 3. Диспут (спор). У участников обычного диалога (в дальнейшем просто диалог) есть совместная цель. Цель определяет инициатор диалога (тот, кто его начал), а вступивший в диалог принимает эту цель. У участников дискуссии и диспута нет общей цели. Как правило, они преследуют разные цели: например, в споре один хочет что-то доказать другому, а другой хочет остаться на своем мнении, защитив его от нападок. В дискуссии один хочет просто высказаться (излить душу), а другой хочет в ответ рассказать о своем опыте/мнении 53. Проблема как форма организации познания. Структура и основные черты проблемы. Логика постановки и решения проблем. Проблема – форма теоретического знания, содержанием которой является то, что еще не познано человеком, но что нужно познать. Иначе говоря, это знание о незнании, вопрос, возникший в ходе познания и требующий ответа.

Весь ход развития человеческого познания может быть представлен как процесс перехода от постановки проблем к их решению, а затем к постановке новых проблем. Научное познание начинается с постановки проблемы. Логическая структура проблемы содержит три элемента: предмет, содержание и объем проблемы Предмет проблемы определяется областью обсуждения. Такой областью может быть отдельно взятая концепция или теория, если имеет место внутренняя проблемная ситуация. Скажем, вопросы соответствия законодательных положений существующим социальным реалиям решаются в рамках того или иного законодательства: уголовного, гражданского и т.д. Эти законодательства являются предметом проблемы. содержание проблемы образуют множества истинных утверждений и принятых логических правил вывода, включенных в парадокс-проблему в качестве аргументов, тезиса и логических форм демонстрации противоречивого доказательства. Объем проблемы - это множество альтернативно возможных предположений относительно ее решения.

Неразвитая проблема (или предпроблема) характеризуется следующими чертами:

1) это нестандартная задача, т.е. задача, для решения которой нет алгоритма (алгоритм неизвестен или даже невозможен). Чаще всего это трудная задача;

2) это задача, которая возникла на базе определенного знания (теории, концепции и т.д.), т.е. как закономерный результат процесса познания;

3) это задача, решение которой направлено на устранение противоречия, возникшего в познании, а также на устранение несоответствия между потребностями и наличием средств для их удовлетворения;

4) это задача, путей решения которой не видно.

Постановка проблемы предусматривает следующий процесс:

отделение фактов объясненных (известных) от фактов, требующих объяснения;

формулировка вопроса, выражающего основной смысл проблемы;

постановка конкретных задач по ее решению.

54. Гипотеза и ее структура. Следственная версия как разновидность гипотезы. Гипотеза – это закономерная форма развития знаний, представляющая собою обоснованное предположение, выдвигаемое с целью выяснения свойств и причин исследуемых явлений. Всякая гипотеза состоит из следующих элементов: 1)основание гипотезы - исходные данные - совокупность фактов или обоснованных утверждений, на которых основывается предположение; 2)форма гипотезы - совокупность умозаключений, которые являются результатом обработки исходных данных и ведут от основания гипотезы к основному предположению; 3)предположение (гипотеза в узком смысле слова) - выводы из фактов и утверждений, выражающих содержание гипотезы; 4)процедура проверки гипотезы, превращающая предположение в достоверное знание или опровергающая его. Следственная версия — это предположение следователя о сущности исследуемого происшествия, о причинах, его вызвавших, о виновных лицах, характере их вины и других обстоятельствах, имеющих значение для установления истины по расследуемому делу. По своей логической природе следственная версия является разновидностью гипотезы. Основное различие между гипотезой и версией состоит в том, что гипотезы выдвигаются на основе обобщенных научных данных по поводу тех или иных значительных явлений природы, крупных проблем общественной жизни и т. д. Версии же строятся по поводу отдельных событий, явлений и фактов. Построение их не связано с фундаментальными научными обобщениями, но в то же время требует научной обоснованности. В процессе расследования следственные версии занимают важное место, являясь основой (ядром) планирования. Они определяют направление расследования, круг вопросов, которые должны быть выяснены. Нужно, однако, всегда помнить, что версия — это предположение, а не доказательство, она говорит о том, что могло быть, а не о том, что было. Версия — лишь форма мышления, помогающая от вероятного идти к достоверному. 55. Построение гипотезы (следственной версии). Логико-методологические требования к гипотезе и следственной версии. Построение гипотез (как и любой версии) - это мыслительный процесс перехода от неполных вероятных знаний к полным и достоверным знаниям. Рассмотрим все этапы построения гипотез (версий). Выдвижение гипотезы включает всестороннее изучение наблюдаемых явлений, анализ и отбор фактов, находящихся в причинно-следственной, временной связи с указанными обстоятельствами, анализ отдельных фактов и отношений между ними. Выдвижение гипотезы (версии) состоит из следующих шагов: Ø    анализ отдельных фактов и отношений между ними; Ø    синтез фактов, их обобщение; Ø    формулировка предположения. Анализ - логический прием, метод исследования, состоящий в том, что изучаемый предмет мысленно или практически расчленяется на составные элементы (признаки, свойства, отношения), каждый из которых затем исследуется в отдельности как часть расчлененного целого. При расследовании преступления анализу подвергается обстановка совершения преступления - фактический материал, который обнаруживается в процессе осмотра места происшествия и его окрестностей, обыска, при ознакомлении с документами, при допросах свидетелей и обвиняемых. Синтез - мысленное соединение частей предмета, расчлененного в процессе анализа, установление взаимодействия и связей частей и познание этого предмета как единого целого. В процессе синтезирования познается нечто новое - взаимодействие частей как целого. При этом проявляется способность следователя правильно связывать факты, выявлять среди них особенное, специфическое. Установление связи между фактами, последовательности их развития позволяет восстановить всю цепь причинной связи, познать факты, лежащие в начале этой цепи и обусловившие появление всех других обстоятельств. Выдвижение предположения осуществляется с помощью логических умозаключений. Гипотеза считается состоятельной, если удовлетворяет следующим логико-методологическим требованиям. 1.Требование объективности. Объективность означает отсутствие предвзятости, т.е. исследователь руководствуется интересами установления истины, а не своими субъективными склонностями, желаниями. 2.Требование всесторонности исследования фактических данных. Всесторонность означает следующее: а)  гипотеза (версия) должна дать объяснение всем собранным фактам без исключения; б)  по каждому обстоятельству причинно-следственной связи явлений (преступления) должны быть построены все возможные гипотезы (версии), по-разному их объясняющие. 3.Гипотеза (версия) должна быть эмпирически и теоретически обоснована и согласована с уже имеющимся знанием. Если факт установлен с достоверностью, то сбор дальнейшего материала можно прекратить. Если полученные выводы с одними фактами согласуются, а другими опровергаются, то необходимо расширить пределы собирания доказательств до устранения или объяснения противоречий 4. гипотеза не должна противоречить установленным знаниям. 5. Гипотеза должна быть принципиально проверяемой, допускать проверку фактами. 6. Гипотеза должна обладать определенной предсказательной и объяснительной силой, способностью отыскивать новые, еще не известные факты и дать им рациональное объяснение. 7. При проверке каждой гипотезы (версии) необходимо стремиться вывести все возможные следствия. Соблюдение этого требования дает возможность максимально конкретизировать общее направление и границы расследования. 8.Все построенные по делу версии проверяются параллельно. При этом необходимо иметь в виду, что при отпадении отдельных версий не следует упускать возможности проверки остальных версий. 56. Проверка гипотезы (следственной версии). Способы проверки. Доказательство гипотез в судебном исследовании. Проверка гипотезы (версии) - целенаправленный сбор доказательств, которые подтверждают или опровергают эти предположения. Теоретический способ проверки гипотезы означает вывод определенных последствий, которые не должны противоречить уже установленным теоретическим положениям (принципам, законам, аксиомам), ее согласованность или непого одженисть с имеющимся теоретическим знаниям на определенном этапе исторического развития наук. Эмпирический способ проверки гипотезы - это подтверждение или неподтверждение последствий, которые выводят из гипотезы по схеме: Г (А л В л С), где Г - гипотеза, А, В, С - возможные последствия Если гипотеза Г под дтверджуеться эмпирическими данными (фактами науки), т.е. не противоречит научным фактам, она приобретает значение истинностного знания

Существует несколько способов подтверждения истинности гипотезы (версии): а)      выведение необходимо вытекающих из гипотезы следствий и их проверка - установление соответствия фактическим данным; б)      непосредственное обнаружение объекта, мысль о существовании которого была основным содержанием гипотезы; в)      дедуктивное выведение гипотезы из другого, но достоверного, знания; г)       подтверждение основания гипотезы, если при построении гипотезы оно не было достоверным; д)      расширение основания гипотезы до пределов, достаточных для достоверного знания, и т. п. При наличии нескольких гипотез по одной и той же проблеме их проверка может осуществляться косвенными путями - по отрицающе-утверждающему и утверждающе-отрицающему модусам разделительно-категорического силлогизма. Опровержение гипотезы осуществляется путем фальсификации вытекающих из нее следствий, т. е. путем установления их несоответствия фактическим данным. Проверка версий - это исследование предположений, которые содержатся в них, на основании объективных данных о конкретные обстоятельства и факты. Проверка должна обеспечивать установление истины по делу, которое расследуется, поэтому она проводится на основании доказательств, полученных в предусмотренном законом порядке. Процесс проверки идет путем как отсеивание ложных версий, так и получения доказательств, которые подтверждают версию, которая соответствует действительности.Проверка версий признается завершенной лишь в том случае, когда собранная совокупность доказательств, которая исчерпывающим образом устанавливает все предусмотренные законом обстоятельства и исключает любые другие объяснения преступного деяния. СПОСОБЫ ДОКАЗАТЕЛЬСТВА ГИПОТЕЗ Рассмотрим два основных способа превращения версий в достоверное знание: (1) непосредственное обнаружение искомых предметов и (2) логическое доказательство версий путем подтверждения следствий. Эти способы используются в судебных исследованиях. (1) Непосредственное обнаружение искомых предметов. Например, при расследовании уголовных дел о хищениях, разбое и т. п. важной задачей судебно-следственных органов является обнаружение приобретенных или накопленных преступным путем вещей, ценностей и денежных сумм. Эти ценности и вещи, как правило, прячутся или реализуются преступниками. В связи с этим и возникают частные версии о местонахождении таких вещей и ценностей. Версии, доказываемые непосредственным обнаружением предполагаемой причины, являются частными версиями. С их помощью, как правило, устанавливаются лишь отдельные фактические обстоятельства дела, частные стороны события преступления. (2) Логическое доказательство версий. Версии, объясняющие существенные обстоятельства расследуемых дел, превращаются в достоверное знание путем логического обоснования. Оно протекает опосредованным путем, так как исследуются события, имевшие место в прошлом, или явления, недоступные непосредственному восприятию. Так доказываются, например, версии о способе совершения преступления, обстоятельствах, при которых было совершено деяние, и т. п. Логическое доказательство гипотезы в зависимости от способа обоснования может протекать в форме косвенного или прямого доказательства.

Косвенное доказательство протекает путем опровержения и исключения всех ложных версий и на этом основании утверждают достоверность единственного оставшегося предположения. Заключение в этом выводе может расцениваться как достоверное, если, во-первых, построен исчерпывающий ряд версий, объясняющих исследуемое событие, и, во-вторых, в процессе проверки версий опровергнуты все ложные предположения. Версия, указывающая на оставшуюся причину, в этом случае будет единственной, а выраженное в ней знание будет выступать уже не как проблематичное, а как достоверное. Этот способ доказательства, протекающий по методу исключения, часто используется в судебно-следственной практике при доказательстве как общих, так и частных версий. Прямое доказательство гипотезы протекает путем выведения из предположения разнообразных, но вытекающих только из данной гипотезы следствий и подтверждения их вновь обнаруженными фактами. 57. Понятие теории. Критерии достоверности теории. Особенности построения логической теории. Роль теории в прогнозировании социальных процессов. Слово «теория» употребляется в широком и узком смысле. В широком смысле теорией называют мышление вообще, когда хотят разграничить мыслительную и предметно-практическую деятельность (теорию и практику). В узком смысле теория представляет собой систему знания, относящуюся к некоторой области действительности или к некоторым аспектам той или иной области действительности. Например, предметом астрономии является особая область реальной действительности – небесные тела; географии и геологии – планета Земля и т.п. ТЕОРИЯ В ЛОГИКЕ представляет собой логически связную систему предложений. В качестве логической связи используются процедуры дедукции, формализующие отношение выводимости. Важной характеристикой теории является степень ее обоснованности, ее практическая подтверждаемость. Основным и наиболее общим критерием истинности теорий считается практика, включающая производственную деятельность, эксперименты и применение теоретических знаний в той или иной деятельности людей. *Вместе с тем практика далеко не абсолютный критерий истинности. Во-первых, этот критерий не всегда применим. Во-вторых, практика может подтверждать и некоторые ложные высказывания (до некоторых пор, например, в опыте подтверждалась теория теплорода). В-третьих, практика лишь подтверждает, но не доказывает истинность теории. Кроме практики, существует логический критерий истинности. Самым важным логическим критерием истинности теорий является их логическая непротиворечивость, т.е. взаимная согласованность утверждений теорий между собой, последовательность в объяснении явлений.  Обычно построение логических теорий осуществляется в специальных искусственных языках, называемых формализованными, предназначенных для точного выражения логических форм высказываний естественного языка. Необходимость использования формализованных языков вызвана тем обстоятельством, что: а) в естественных языках нет четких синтаксических критериев правильности построения выражений; б) грамматическая структура высказываний не всегда соответствует их логической форме; в) выражения естественного языка многозначны и допускают различные трактовки. Построения формализованного языка обычно начинается с построения алфавита – совокупности простейших исходных символов, включающих 1) логические символы (символы логических терминов); 2) нелогические символы (предназначенные для замещения простых высказываний или нелогических терминов различных категорий); 3) технические символы (напр., скобки). Следующим шагом является задание допустимых интерпретаций (семантики) для каждого вида нелогических символов алфавита. Для каждого вида правильно построенных выражений формулируются правила приписывания им значений при произвольной интерпретации нелогических символов, входящих в их состав. В частности, определяются условия истинности и условия ложности формул различных типов. При этом задается точный смысл логических символов алфавита и построение языка на этом заканчивается. 58. Модель как средство теоретического выражения знания. Логический характер построения модели. Проблема использования идеализированных объектов в гуманитарных науках, в юридической теории и практике. Под моделью знаний понимается способ описания знаний в базе знаний. Логическая модель представления знаний. В основе моделей такого типа лежит формальная система, задаваемая четверкой вида: М = < Т, Р, А. В >. Множество Т– это множество базовых элементов. Например, это могут быть слова из какого то ограниченного словаря или детали конструктора. Для множества Т существует некоторый способ определения принадлежности или непринадлежности произвольного элемента к этому множеству. Процедура такой проверки может быть любой, но за конечное число шагов она должна давать ответ на вопрос, является ли х элементом множества Т или нет. Множество Р– это множество синтаксических правил. С их помощью из элементов множества Т образуют синтаксически правильные совокупности (СПС). Например, из слов словаря строятся синтаксически правильные фразы, из деталей конструктора собираются новые механизмы. Существует процедура, с помощью которой за конечное число шагов можно определить, является ли совокупность Х синтаксически правильной. В множестве синтаксически правильных совокупностей выделяется некоторое подмножество А. Элементы множества А называются аксиомами. Аксиомы составляют ядро предметной области. Существует процедура, с помощью которой для любой СПС можно получить ответ на вопрос является ли она аксиомой. Множество В– это множество правил вывода. Применяя их к элементам множества А, можно получать новые СПС, к которым снова можно применять правила из множества В. Так формируется множество выводимых в данной формальной системе совокупностей. Если имеется процедура, с помощью которой можно определить для любой СПС, является ли она выводимой, то такая формальная система называется разрешимой. Правила вывода являются самой сложной частью логической модели. На практике логическая модель чаще всего используется в системе логики предикатов и выведения заключений с помощью силлогизмов. Предикатом или логической функцией называется функция от любого числа аргументов, принимающих истинное значение И(1) и Л(0). Аргументы принимают значения из произвольного конечного или бесконечного множества М, называемого предметной областью. Предикат от n-аргументов является n-мерным предикатом. Силлогизм – это заключение. С помощью силлогизмов из двух суждений выводится третье. Например: - все металлы электропроводны; - медь – металл. Заключение – медь электропроводна. В любом языке для создания языковых форм должно быть определено следующее; множество знаков, которые можно в нем использовать; полное определение слов через знаковые последовательности; грамматические правила образования предложений из слов (семантические правила). Каждое слово из предложения соответствует объектам и действиям того реального мира, который описывается этим языком. Таким образом, в языке присутствуют слова, которые описывают сущности, и слова, которые описывают атрибуты сущностей и действия над ними. 59. Закон исключенного третьего. Формула закона исключённого третьего: из двух противоречащих мыслей одна является истинной, а вторая ложной; третьего не дано (закону исключённого третьего подчиняются только противоречащие мысли). Закон исключённого третьего — закон классической логики, состоящий в том, что из двух высказываний — «А» или «не А» — одно обязательно является истинным, то есть два суждения, одно из которых является отрицанием другого, не могут быть одновременно ложными.  Хоть небольшое, но хорошее подспорье для молодой семьи.  Здесь не соблюдается третий закон логики – закон исключенного третьего. Как мы помним, непременное условие соблюдения третьего закона логики – то, что сопоставляемые высказывания должны быть действительно противоречивыми, т. е. такими, между которыми нет и не может быть среднего, третьего, промежуточного понятия. Они должны исключать друг друга. Небольшое и хорошее никак не являются противоположными. 60. Закон противоречия. Закон непротиворечия гласит: два суждения, из которых в одном утверждается нечто о предмете мысли («А есть В»), а в другом то же самое отрицается об этом же предмете мысли («А не есть В»), не могут быть одновременно истинными, если при этом признак В утверждается или отрицается о предмете мысли А, рассматриваемом в одно и то же время и в одном и том же отношении. Например, суждения «Данная река – приток Волги» и «Данная река не является притоком Волги» не могут быть одновременно истинными, если эти суждения относятся к одной и той же реке. Противоречия не будет, если мы что-либо утверждаем и то же самое отрицаем относительно одного и того же лица, которое, однако, рассматривается в разное время. Так, суждения «Данный человек – футболист» и «Данный человек – не футболист» могут быть одновременно истинными, если в первом из них имеется в виду одно время (когда данный человек действительно был футболистом), а во втором – другое (когда он перестал играть в футбол). Закон непротиворечия читается так: ≪Два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении≫. 61. Закон достаточного основания. Формулировку данного закона можно выразить следующим образом; для того чтобы считаться вполне достоверным, всякое положение должно быть доказано, т.е. должны быть известны достаточные основания, в силу которых оно считается истинным. Достаточным основанием может быть другая, уже проверенная практикой, признанная истинной мысль, необходимым результатом которой является истинность доказываемого положения. В науке достаточными основаниями считаются: а) положения об удостоверенных фактах действительности, б) научные определения, в) ранее доказанные научные положения, г) аксиомы, а также д) личный опыт. 62. Закон эквивалентности. Закон тождества утверждает, что любая мысль обязательно должна быть равна (тождественна) самой себе, т. е. она должна быть ясной, точной, простой, определенной. Этот закон запрещает путать и подменять понятия в рассуждении (т. е. употреблять одно и то же слово в разных значениях или вкладывать одно и то же значение в разные слова). Например, Из-за рассеянности на турнирах шахматист неоднократно терял очки. то ли шахматист терял очки как прибор для зрения, то ли – как спортивные баллы; две нетождественные ситуации представляются в этом высказывании как тождественные.