
Лекции
.pdf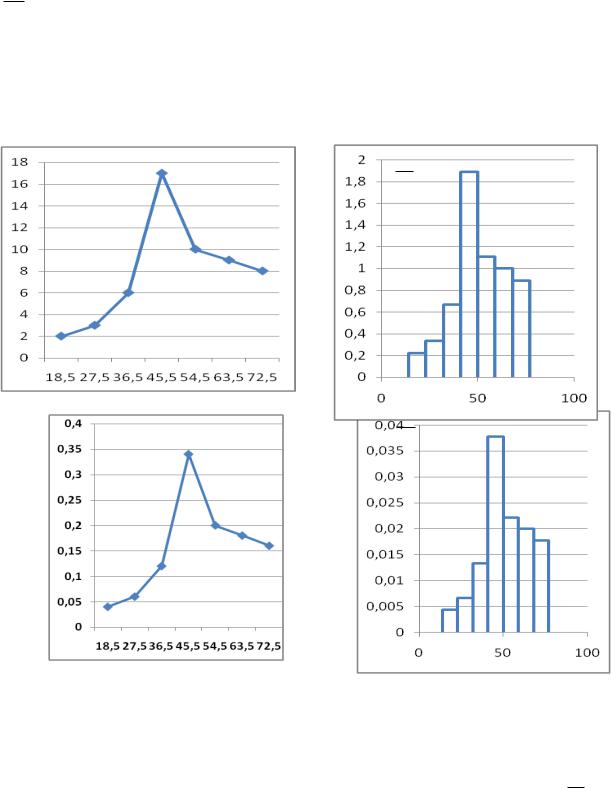
относительная частота |
|
|
(высоты прямоугольников гистограммы будут равны |
||
i |
|||||
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
, а площадь всей гистограммы относительных частот равна единице). |
||||
h |
|||||
|
|
|
|
||
Пример 3. Построить полигон и гистограмму частот и относительных частот по группированной выборке примера 2.
Решение. По результатам группировки (см. таблицу примера 2) строим на рисунках 1,2,3,4, расположенных далее, соответственно полигон частот, гистограмму частот, полигон относительных частот и гистограмму относительных частот.
|
|
|
|
n |
ni |
||
i |
|||
|
|
|
|
|
i |
||
|
xi
n |
|
|
i |
||
|
||
9 |
||
x |
|
|
i |
||
|
14 |
|
|
|
|
|
i |
||
|
||
9 |
||
x |
|
|
i |
||
|
23
32 41
14 23 32
41
59 68
59
x |
i |
|
77
68 |
77 |
|
Если известно распределение частот какого-нибудь количественного при-
знака X, нетрудно заметить, что и частота ni
и относительная частота
|
|
|
n |
i |
|
|
|||
|
|
|
|
|
|
i |
|
n |
|
|
|
|
||
за-
висят от xi . Из этих соображений вводится так называемая эмпирическая функция

распределения F (x) , которая каждому значению |
x |
сумму относительных частот вариант выборки, меньших
X
x:
ставит в соответствие
F (x) ni .
xi x n
Иногда функция
F |
|
(x) |
|
записывается как
F |
|
(x) |
n |
x |
|
||||
|
n |
|||
|
|
|
||
, где под
n |
x |
|
понима-
ется суммарная частота всех вариант выборки, меньших x . Эмпирическая функция
распределения |
F |
|
(x) |
позволяет составить представление об интегральной функ- |
|
ции распределения |
F(x) |
всей генеральной совокупности признака X ( |
F(x) |
- в |
||||
|
|
|||||||
этом случае называется обычно теоретической функцией распределения). |
|
|
||||||
Эмпирическая функция распределения |
F |
|
(x) |
обладает всеми свойствами |
||||
|
||||||||
|
|
|
||||||
интегральной функции распределения:
1. значения эмпирической функции распределения принадлежат отрезку [0;1], т.е.
для любого |
x X , 0 F |
|
(x) 1 |
; |
|
2. |
F |
|
(x) |
- неубывающая функция; если |
x |
- наименьшая варианта, то для |
||||
|
||||||||||
|
|
|
|
1 |
||||||
F |
|
(x) 0 , а если xk - наибольшая варианта, то для |
x xk , F |
|
(x) 1 |
|||||
|
|
|||||||||
x
x1
,
Пример 4. Построить графики эмпирических функций распределения по исходной и группированной выборке примера 2.
Решение. Запишем исходные данные в виде статистического распределения:
x |
i |
14 |
21 |
28 |
30 |
32 |
33 |
35 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
i |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
3 |
1 |
1 |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
i |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
57 |
58 |
59 |
60 |
61 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
1 |
2 |
2 |
2 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
i |
65 |
67 |
68 |
72 |
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
i |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как x1 =14, а x50 =77, то
F |
|
(x) |
|
=0 при
x 14
и
F |
|
(x) |
|
=1 при
x
77
.
На полуинтервале (14;77] эмпирическую функцию распределения строим с использованием статистического распределения:
При 14 x 21,
при 21 x 28, при 44 x 45 ,
F (x) 1 50 0,02 ;
F |
|
(x) 2 50 |
0,04 |
; …; |
||||
|
|
|||||||
|
|
|
|
|
|
|
||
F |
|
(x) 20 50 |
0,4 |
и т.д. |
||||
|
|
|||||||
|
|
|
|
|
|
|
|
|
Аналогично строится график лицу примера 2 ). В этом случае F
F |
|
|
(x)
(x) |
по сгруппированным данным (см. таб- |
|
имеет скачки в серединах интервалов, а их
величина определяется значениями накопительных относительных частот из последней графы таблицы.
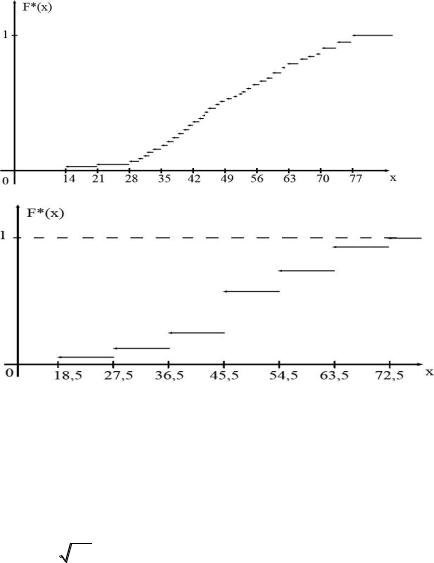
Рис.1
Рис.2
3. Точечные оценки параметров распределения.
Пусть изучаемая нами случайная величина X определяется множеством параметров 1, 2... .
Например, параметрами нормального распределения с плотностью вероят-
|
|
|
|
|
|
|
1 |
|
e |
x a 2 |
|
|
ности |
f |
x |
|
|
|
2 2 |
являются |
|
||||
|
|
|
||||||||||
|
|
|
|
2 |
|
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
распределения с плотностью вероятности
a, |
2 |
|
|
f x |
|
, параметром показательного
e |
x |
является |
|
. |
|
|
|||
|
|
1 |
Пусть параметры распределения нам неизвестны. Используя выборку наблюдений можно вычислить приближенные значения параметров, то есть их оценки. Эти оценки меняются при переходе от одной выборке к другой, то есть оценки параметров есть некоторые случайные величины, зависящие от выборки, и, следовательно, они имеют свои собственные распределения.
Оценки параметров распределения получают с помощью специально построенных статистик.
Статистикой называется всякая функция, зависящая от выборки. Оценка параметра , даваемая одним числом , называется точечной. Как правило, для получения оценки параметра можно использовать не-
сколько различных статистик. При этом получаются различные значения оценок параметра. Качество оценок будем характеризовать следующими основными свойствами: несмещенность, состоятельность, эффективность.
Пусть X1, X2 ,..., Xn - выборка из параметрического семейства распределе-
ний.
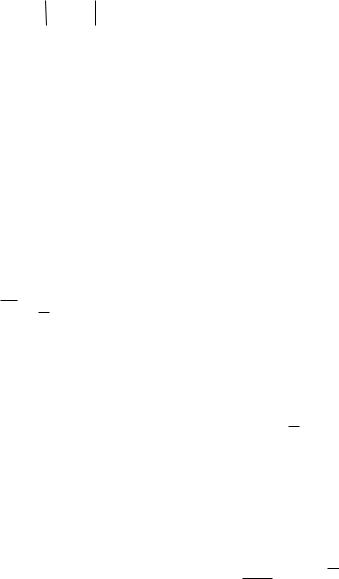
|
называется несмещенной оценкой параметра , если математи- |
Оценка n |
ческое ожидание оценки совпадает с оцениваемым параметром, т.е. при любом
объеме выборки выполняется условие |
|
. |
M n |
||
Оценка называется состоятельной, |
если при увеличении объема выборки |
|
n |
|
|
n
бого
|
сходится по вероятности к оцениваемому параметру, т.е. для лю- |
||||
оценка n |
|||||
0, lim p n |
|
1 |
|
p |
|
|
(или коротко n |
). |
|||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть n1 |
и n 2 две различные несмещенные оценки параметра . Оценка |
||||||||||
|
|
|
|
|
|
|
|
|
D |
|
|
D |
|
|
|
|
|
|
|
|
|||||||
|
n1 |
называется более эффективной, чем |
|
n 2 |
, если |
n1 |
n2 . |
||||||
|
|
|
|
||||||||||
|
|
Несмещенная состоятельная оценка |
|
|
параметра |
|
называется эффектив- |
||||||
|
|
|
|
||||||||||
ной, если она имеет наименьшую возможную дисперсию при заданном объеме вы-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
, где |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
борки, то есть |
D |
|
min D |
|
|
|
- множество всех оценок параметра при |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
фиксированном объеме выборки |
n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Пусть изучаемая случайная величина |
X |
имеет неизвестные нам математиче- |
||||||||||||||||||||||||||||||||||||||||||||||||
ское ожидание |
M |
X |
m |
и дисперсию |
D X |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Найдем точечные оценки для |
M X и |
D X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Теорема 1. Пусть |
|
X1, X |
2 ,..., Xn |
- выборка объема |
|
n , тогда случайная вели- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чина |
m |
* |
x |
|
|
|
X |
|
|
|
|
является несмещенной, |
|
состоятельной и эффективной |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
в |
|
|
|
|
i |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
оценкой для |
|
M |
X m |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Случайная величина X в |
называется средним выборочным. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
m |
|
|
|
||||||||||
|
Теорема 2. Случайная величина |
2 |
|
|
|
|
X |
|
является смещен- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
â |
|
|
i |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
||
ной оценкой дисперсии |
|
D X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Случайная величина |
|
|
|
называется выборочной дисперсией и обозначается |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Dв . Из теоремы 2 следует, что выборочная дисперсия является смещенной оценкой |
|||||||||||||||||||||||||||||||||||||||||||||||||||
для дисперсии |
D x |
|
2 |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
Теорема 3. Случайная величина |
S |
2 |
|
|
|
|
X |
|
|
является несмещенной |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
i |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
оценкой дисперсии D X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Таким образом, |
M s |
2 |
|
2 |
и |
s |
2 |
- несмещенная оценка для |
|
|
2 |
. |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Случайная величина S 2 |
|
|
|
|
1 |
|
xi |
|
X |
в |
называется исправленной выбороч- |
|||||||||||||||||||||||||||||||||||||||
|
|
n 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной дисперсией. Выборочная дисперсия и исправленная выборочная дисперсия
связаны соотношением s2 |
n |
|
2 . |
|
n 1 |
||||
|
|
|||

персии
Замечание. Можно доказать, что
D X .
s |
2 |
|
является состоятельной оценкой дис-
Пример. Имеются следующие данные об урожайности пшеницы на 7 опытных участках одинакового размера (ц/га): 26,5;26,2;30,1;32,3;29,1;25.
Найти несмещенные состоятельные оценки для Решение.
M
x
и
D x
.
|
|
|
|
|
|
|
|
1 |
n |
|
1 |
26,5 |
|
|
|
|
m |
* |
X в |
xi |
|
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
n |
7 |
||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
i |
|
|
|
|
|
|
|||
S |
|
|
|
|
x m |
|
|
|
|
|
|
||
|
n 1 |
|
|
|
|
|
|
|
|
||||
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 26,5 27,93 2 26, 2 27,93 2 6
25,2 30,1 32,3 29,1 25 27,93 |
(ц/га). |
|
30,1 27,93 |
2 |
32,3 27,93 |
2 |
29,1 27,93 |
2 |
25 27,93 |
2 |
|
7,11. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
4. Интервальные оценки параметров статистического распределения
При малом числе наблюдений замена неизвестного параметра его точеч-
ной оценкой |
|
может привести к значительным ошибкам. Кроме того, в ряде за- |
|
дач требуется не только найти для параметра приближенные значения, но и оценить его точность и надежность. В этих случаях возникает задача о приближении
|
|
, |
2 . |
|
|
|
|
|
параметра не одним числом, а целым интервалом 1 |
|
|
|
|
|
|||
Интервальной оценкой параметра называется интервал l1,l2 |
, который с |
|||||||
вероятностью содержит оцениваемый параметр, то есть P l1 l2 |
. |
|
||||||
l |
,l |
|
|
|
|
|
||
Интервал 1 |
2 называется доверительным интервалом, вероятность |
|
||||||
называется доверительной вероятностью или надежностью, число |
l |
l |
|
|||||
2 |
1 |
назы- |
||||||
2 |
||||||||
|
|
|
|
|
|
|||
вается точностью интервальной оценки. |
|
|
|
|
|
|
||
Доверительная вероятность обычно задается заранее. Чаще всего значение |
||||||||
равно 0,9;0,95;0,99. Отметим, что концы доверительного интервала |
l1 |
,l2 явля- |
||||||
ются случайными величинами, меняющимися при переходе от выборки к выборке.
Общая схема построения доверительного интервала состоит из следующих этапов.
1. На базе исследуемой случайной величины X с распределением, зависящим от параметра , строится с помощью выборки новая случайная величина –
статистика |
Z |
, распределение которой полностью известно и не зависит от пара- |
|
|
метра .
2. Находится интервал 1 2 такой, что P 1 Z , где - доверитель-
ная вероятность.
3. Разрешая неравенство 1 Z 2 относительно параметра , получаем эквивалентное неравенство l1 l2 . Так как P l1 l2 , то следовательно, интервал l1,l2 - искомый доверительный интервал.
Построим доверительные интервалы параметров нормального распределе-
ния. |
N m, |
Пусть X |
независимая выборка
2
x1
, доверительная вероятность задана и равна
, x2 ,..., xn .
, получена
Построение доверительного интервала для математического ожидания нормально распределенной случайной величины, дисперсия которой из-
вестна: |
|
X в m |
|
|
||
1. |
Рассмотрим статистику Z |
|
n ~ N 0,1 |
|||
|
||||||
|
|
|
|
|
||
2. |
Если |
P z , то по свойству U1 . Таким образом, |
||||
|
|
|
|
|
2 |
|
|
U1 |
|
|
|
P |
Z U1 |
. |
||
|
2 |
2 |
|
|
3. разрешаем неравенство относительно неизвестного параметра
m
.
U |
1 |
|
|
|
|
||
|
2 |
|
|
|
|
в |
|
P X |
|||
|
|
|
|
|
|
|
|
X |
â |
m |
n |
|
|
|
|
||
|
|
|
||
|
|
|
||
|
U |
|
|
|
|
n |
1 y |
||
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
U1 , отсюда |
X в |
|||
2 |
|
|
|
|
m X в |
|
U |
|
|
|
|
|
||
|
n |
|
1 y |
|
|
|
|
2 |
|
|
U |
|
m X в |
|
U |
|
, причем |
n |
1 y |
n |
1 y |
||||
|
2 |
|
|
2 |
|
||
|
|
|
|
|
|
||
, то есть получен доверительный ин- |
|||||||
тервал для параметра |
m . |
|
|
|
m |
- точечная оценка для параметра m , то формула для дове- |
Так как X |
â |
|||
|
|
|
|
|
рительного интервала параметра |
m при известном окончательно может быть за- |
|
|
|
|
|
|
|
|
|
|
|
|
U1 m m |
|
|
|
|
||
писана следующим образом |
m |
|
|
U1 , причем |
||||||||||||||
|
n |
|
n |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P m |
|
|
U1 |
m m |
|
|
|
U1 . |
|
|
|
|
||||||
|
n |
|
|
n |
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
Пример. Пусть дисперсия нормально распределенной случайной величины |
||||||||||||||||||
X равна 0, 25 |
. По выборке объема n 25 найдена точечная оценка математиче- |
|||||||||||||||||
ского ожидания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
m 52 . Найти доверительный интервал для неизвестного мате- |
||||||||||||||||||
матического ожидания |
m , если доверительная вероятность 0,95 . |
|||||||||||||||||
Решение. |
1 |
|
1 0, 95 |
0, 975 . По таблице квантилей нормального рас- |
||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
пределения находим
U |
1 |
|
|
|
2 |
U |
0,975 |
|
1,96
. Следовательно, доверительный интервал
|
|
|
0, 25 |
1, 96 |
m 52 |
0, 25 |
1, 96 |
|
||||
имеет вид |
52 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||
|
|
|
25 |
|
|
|
25 |
|
|
|
||
P 51,804 m 52,196 0,95 .
или
51,804
m
52,196
, причем
Построение доверительного интервала для математического ожидания нормально распределенной случайной величины при неизвестной дисперсии.
|
|
|
|
|
|
|
|
1) Рассмотрим статистику Z |
|
|
|
X в m |
~ T n 1 (см. теорему 1 из 3.3) |
||
n |
|||||||
|
|
|
S |
||||
|
|
|
|
|
|
||
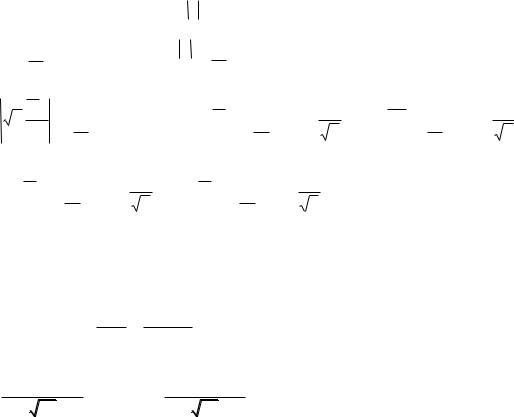
2) |
Найдем |
|
такое, что |
P z |
|
. По свойству 2 квантилей из |
||||||
|
t1 |
n 1 , так что |
|
|
|
|
|
|
|
|||
|
P z t1 n 1 |
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
3) |
Разрешая |
неравенство |
относительного |
|
параметра |
m , |
||||||
|
n |
X в |
|
t |
1 y n 1 . Отсюда |
X в t1 y n 1 |
s |
m X в |
t1 y |
n 1 |
||
|
s |
|
n |
|||||||||
|
|
|
|
2 |
|
|
2 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
3.4 имеем
получим.
s |
. При- |
|
n |
||
|
чем
|
|
n 1 |
s |
P X в t |
1 y |
|
|
|
|
n |
|
|
2 |
|
m X в t |
|
n 1 |
s |
|
|
1 y |
|
|
|||
|
|
|
|
|
|
|
2 |
|
n |
|
|
. Полученный интервал яв-
ляется искомым доверительным интервалом. |
|
|||
Пример. По выборке объема n 20 |
из нормальной генеральной совокупно- |
|||
|
s |
2 |
13,34 |
. Найти доверительный интер- |
сти получены точечные оценки m 621 и |
|
|||
вал для параметра m при 0,95 .
|
|
|
Решение. |
1 |
|
1 0, 95 |
0, 975 . |
||
|
|
|
2 |
|
2 |
||||
t0,975 19 2, 093. |
|
|
|
|
|||||
|
Доверительный |
||||||||
|
621 |
|
2, 09313, 34 |
m 621 |
2, 09313, 34 |
|
|||
|
20 |
|
20 |
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
P 614, 75 m 627, 25 0,95 . |
|
|
|||||||
По |
таблице |
квантилей Стьюдента |
|
|
интервал |
имеет |
вид |
или |
614, 75 m 627, 25 , |
причем |
|
