Добавил:

ukusezha Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Прикладные задачи математической статистики

Файл:

Лекции

.pdf

Скачиваний:

Добавлен:

15.03.2025

Размер:

6.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Пример. Среднее значение длины детали равно 50 см., а дисперсия равна 0,1. Оценить вероятность того, что изготовленная деталь окажется по своей длине не

меньше 49,5 и не больше 50,5 см.
Решение:
Так как а=50, то условие	X	, в котором случайная величина X

обозначает возможную длину детали, приводится почленным вычитанием числа

а=50 к виду	X a	0,5
	X a	0,5

Применяя неравенство (4) в случае ε = 0,5, D(X)=0,1, получим
		P( X 50 ) 1	0,1
		P( X 50 ) 1	(0,5)	2
				2

Теорема Чебышева


Если случайные величины				X	, X	2	,
Если случайные величины				1		2
и дисперсии	D(X	)	, ограниченные одним и
и дисперсии	i		, ограниченные одним и

ε > 0 выполняется неравенство:

..., X	n независимы, имеют	M ( X	) a
	n независимы, имеют	i

тем же числом С, то для любого числа

	1	n
	1	X i
		X i
	n
		i 1

1 n ai

n i 1


	1

C		(5)
n	2	(5)
n

то есть

	1		n			1	n
lim P					i		i	1
lim P		n i 1		X			a	1
n		n i 1				n i 1
n

Пример. Для определения средней урожайности поля площадью 1800 га

взяли на выборку по 1 м	2	с каждого гектара. Известно, что по каждому гектару поля

дисперсия не превышает 6. Оценить вероятность того, что отклонение средней выборочной урожайности отличается от средней урожайности по всему полю не более чем на 0,25

Решение:

Воспользуемся неравенством (5) при n=1800, С=6, ε = 0,25:

	1	n			1	n		6
P			X	i		a	1		2
	1800			i	1800	i	1800	(0, 25)	2
	1800	i 1			1800	i 1	1800	(0, 25)
		i 1				i 1

Таким образом, вероятность

	1	n
P		X i
	1800 i 1

1800 ai

Теорема Бернулли

Если в каждом из независимых испытаний вероятность р появления собы-

тия А постоянна, то вероятность того, что отклонение относительной частоты m от n

вероятности р по модулю не превзойдёт числа ε > 0,больше, чем разность 1 npq2 ,

	m				pq
то есть	P		p	1			(6) .
		n			n	2

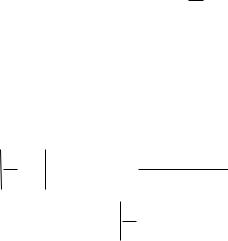
Отсюда следует, что

lim P	m	p	1
	m
	n

n
n

Пример. При штамповке пластинок из пластмассы брак составляет 3%. Найти вероятность того, что при проверке партии в 1000 пластинок выявится отклонение от установленного процента брака меньше, чем на 1%.

Решение: Из условия задачи следует, что n=1000, ε = 0,01, p=0,03, q=1-p=0,97. В соответствии с формулой (6), получим:

P	m		p	1	0, 03 0,	97
		n			1000 (0, 01)		2

Следовательно,

	m
	n
	n

Рассмотрим понятиие о центральной предельной теореме, которую также называют теоремой Ляпунова. Её суть состоит в том, что если случайная величина 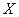является суммой очень большого числа взаимно независимых случайных величин

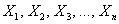, влияние каждой из которых на всю сумму ничтожно мало, то 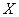имеет распределение, близкое к нормальному.

В окружающем мире условие теоремы Ляпунова выполняется очень часто, и поэтому нормальное распределение (близкое к нему) и встречается буквально на каждом шагу.

Так, например, молекул воздуха очень и очень много, и каждая из них своим движением оказывает ничтожно малое влияние на всю совокупность. Поэтому скорость молекул воздуха распределена нормально.

4. Двумерные случайные величины, их числовые характеристики

Часто результат опыта описывается не одной случайной величиной X, а не-

сколькими случайными величинами:

, X

,..., X

В этом случае принято говорить, что указанные случайные величины обра-

зуют систему (

, X

,..., X

n. ). Систему двух случайных величин (X,Y) можно

изобразить случайной точкой на плоскости.

Закон распределения системы двух дискретных случайных величин может быть задан с помощью таблицы:

X\Y	y1	y2	…	yn
x	p	p	…	p
1	11	12		1n

x2	p21	p22	…	p2n
…	…	…	…	…

xm	pm1	pm2	…	pmn

m	n
ij		1
	p	1
i 1	j 1

Функцией распределения двумерной случайной величины (X,Y) называется функция F(x,y)=P(X<x, Y<y).

Геометрически функция F(x,y) интерпретируется как вероятность попадания случайной точки (X,Y) в бесконечный квадрат с вершиной в точке (x,y), лежащий левее и ниже ее.

Вероятность попадания случайной точки в прямоугольник со сторонами, параллельными координатным осям:

( 1 ≤ ≤ 2, 1 ≤ ≤ 2) = ( 2, 2) − ( 1, 2) − ( 2, 1) + (1, 1)

Закон распределения системы двух непрерывных случайных величин (X,Y) будем задавать с помощью функции плотности вероятности f(x, y).

Помимо функции F(x,y), для двумерной непрерывной СВ вводится понятие

функции плотности распределения вероятностей, которая определяется как сме-

шанная производная 2-го порядка от функции распределения:

Вероятность попадания случайной точки (X,Y) в область D:

P[( X ,Y ) D] f (x, y)dxdy

Функция плотности вероятности обладает следующими свойствами:

1. f (x, y) 0

2.
2.		f (x, y)dxdy 1
		f (x, y)dxdy 1

Если все точки (X,Y) принадлежат конечной области D, то последнее условие при-

нимает вид: f (x, y)dxdy 1

По стандартной формуле:

Математические ожидания дискретных случайных величин X и Y, входящих в систему, определяются по формулам:

m n

mx M ( X ) xi pij ,

i 1 j 1

		m	n
m	M (Y )			y p
y				j ij
		i 1	j 1

Математические ожидания непрерывных случайных величин X и Y:


mx	M ( X ) xf (x, y)dxdy


my	M (Y ) yf (x, y)dxdy

Точка		m	; m	y	является центром рассеивания системы случайных вели-
		x

чин (X,Y).

Дисперсии дискретных случайных величин X и Y, определяются по формулам:

D( X )

D(Y )

pij (xi i 1 j 1

pij ( y j i 1 j 1

mx )2

my )2

;

Дисперсии непрерывных случайных величин X и Y, определяются по формулам:


D( X ) (x mx )	2	f (x, y)dxdy
D( X ) (x mx )		f (x, y)dxdy


D(Y ) ( y my )	2	f (x, y)dxdy
D(Y ) ( y my )		f (x, y)dxdy

Средние квадратические отклонения:

	x

D(X )

	y		D(Y )
	y

Для вычисления дисперсий также могут быть применены формулы:

D( X )

M ( X

2	)

M ( X ) 2

, D(Y ) M (Y 2 ) M (Y ) 2

5. Ковариация и коэффициент корреляции случайных величин.

Важную роль в теории систем случайных величин играет так называемый корреля-

ционный момент (ковариация):

cov( X ,Y ) M[( X m )(Y m

)]

Для дискретных случайных величин X и Y корреляционный момент находится по

формуле:

cov(X ,Y )

(x m )(y m

m n

а для непрерывных – по формуле:

cov( X ,Y )

(x m

)( y m

) f (x, y)dxdy

Корреляционный момент можно также найти по формуле:

cov(X ,Y ) M (XY ) M (X )M (Y)

Здесь M ( XY ) xn ym pmn

- для дискретных случайных величин X и Y.

m n

Для непрерывных случайных величин X и Y: M ( XY ) xyf (x, y)dxdy

Для характеристики связи между величинами X и Y рассматривается так называе-

cov( X ,Y )

мый коэффициент корреляции: xy

( X ) (Y )

Коэффициент корреляции является безразмерной величиной и удовлетворяет условию 1 rxy 1.

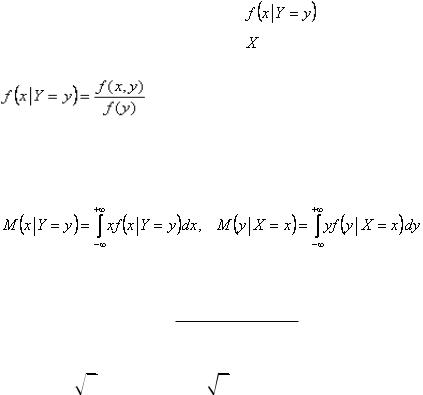
Две случайные величины являются независимыми, если закон распределения одной из них не зависит от того, какое значение значения приняла другая случайная величина. Например, случайные погрешности измерений X,Y двух независимо работающих измерительных приборов.

Если же СВ зависимы, то закон распределения одной величины зависит от того, какое значение приняла другая величина. Например: 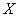– рост случайно выбранного человека, 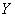– его вес. Ну, или наоборот, сначала смотрим на вес, а затем анализируем закон распределения роста.

Условные законы распределения случайных величин обозначаются следующим об-

разом: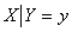 – условный закон распределения СВ X, при условии, что СВ Y примет (или уже приняла) какое-либо конкретное значение y.

– условный закон распределенияY, при условии, что X примет или уже приняла некоторое конкретное значение x.

В случае независимости случайных величин все условные законы 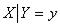будут совпадать с законом распределения случайной величины X (ибо «игрековая» вели-

чина никак не влияет на «иксовую»), и все условные законы 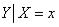– совпадать с законом Y.

Плотность распределения	называют условной плотностью распре-
деления случайной величины	. Данная функция определяется по формуле:

Аналогично, 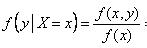Условные математические ожидания рассчитываются по формулам:

Пример. Система двух

с плотностью

f ( x, y )

Примеры решения задач.

случайных величин (X, У) подчинена закону распределения

		1
2	(1 x	2	)(1	y	2	)

Определить вероятность попадания случайной точки в прямоугольник с вершинами

К(1;1), L( 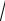3 ;1), M(1;0), N( 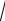3 ;0).

Решение: P[( X ,Y ) D] f (x, y)dxdy

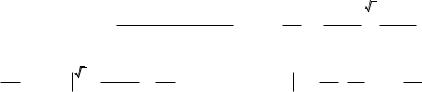
P[( X ,Y ) D]													1						1		1			1				3		dx
													1					dxdy	1					1						dx		dy
								2		(1 x			2	)(1	y		2	dxdy		2		1	y			2			1	x	2	dy
										(1 x				)(1	y			)				1	y						1	x
	1					D					1										0	1					1				1
	1			3	1		dy				1									1		1									1
		2	arctg x 1			1	y		2			2				4		arctg y 0					2		12				4
					0	1	y							3		4									12				4	48
					0

Пример. Задан закон распределения системы случайных величин:

X\Y	0	1

-1	0	0,2

0	0,1	0,1

1	0,5	0,1

Найти законы распределения случайных величин X, Y и условный закон распределения случайной величины X при условии, что Y=0. Найти вероятность того, что X примет значение, меньшее, чем Y.

Решение: Случайная величина X может принимать значения:

X = -1 с вероятностью р1 = 0+0,2 = 0,2;

X = 1 с вероятностью р2= 0,1+0,1 = 0,2;

X = 1 с вероятностью р3= 0,5+0,1= 0,6, то есть её закон распределения:

		x	-1	0	1
		i

		p	0,2	0,2	0,6
		i

Аналогично, закон распределения случайной величины Y:

	y	j	0	1
		j

	p j		0,6	0,4

Условный закон распределения случайной величины X при условии, что Y = 0, получим, если вероятности, стоящие в столбце при Y = 0, разделим на их сумму (то есть р (Y = 0) = 0,6). Получим

	x	-1	0		1
	i

	p j (xi )	0		1		5
	p j (xi )		6		6
			6		6

Для нахождения Р(X<Y) складываем вероятности событий					pij из данной таблицы,
для которых xi y j . Получим:		Р(X<Y)=0+0,2+0,1=0,3.

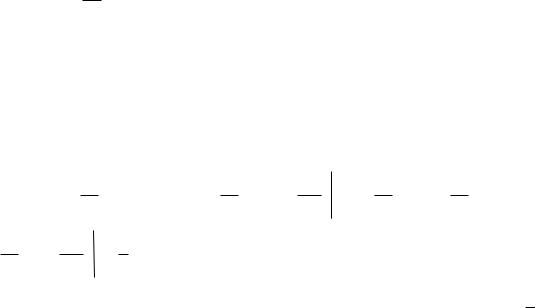
Пример. Система случайных величин (X,Y) подчинена закону распределения с плотностью

	1	(x y)	в области D;
		(x y)	в области D;
f (x, y)	27
	0,	вне этой области
	0,	вне этой области

Область D – это квадрат, ограниченный прямыми: x=0, x=3, y=0, y=3.

Найти математические ожидания	m	x	и	m	y .

Решение:

m		M ( X
x
		1		3
			x

	27


mx		M ( X ) xf ( x,					y)dxdy

		1	3	3		1	3		xy	2	3		1	3		9x
			3	3			3			2				3

)					x(x y)dxdy			x2 y				dx			3x2
)					x(x y)dxdy			x2 y				dx			3x2		dx
	27 0 0					27 0			2		0		27	0		2
											0
9x	2		3		7
	2

4					4
4			0		4
			0

Аналогично, по формуле


my	M (Y ) yf (x, y)dxdy

находим

m	M (Y )	7

y		4

Пример. В двух ящиках находятся по 6 шаров; в 1-м ящике: 1шар – с №1, 2 шара – с №2, 3 шара – с №3; во 2-м ящике: 2шара – с №1, 3 шара – с №2, 1 шар – с № 3. Пусть X – номер шара, извлечённого из первого ящика, Y – номер шара извлечённого из второго ящика. Из каждого ящика извлекли по шару. Составить таблицу закона распределения системы случайных величин (X,Y).

Решение:

Случайная точка (1;1) имеет кратность 1 2=2; Случайная точка (1;2) имеет кратность 1 3=3;

точка (1;3) ---------------------	1 1=1;
точка (2;1) ---------------------	2 2=4;
точка (2;2) ---------------------	2 3=6;
точка (2;3) ---------------------	2 1=2;
точка (3;1) ---------------------	3 2=6;
точка (3;2) ---------------------	3 3=9;
точка (3;3) ---------------------	3 1=3;

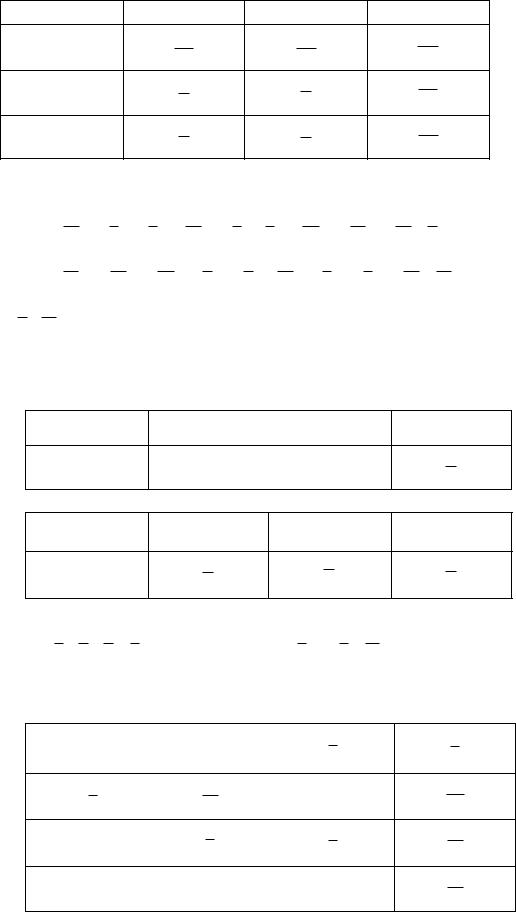
Всего случайных точек 6 6=36 Так как отношение кратности точки ко всему количеству точек равно вероятности

появления этой точки, то таблица закона распределения системы случайных величин имеет вид:

X\Y

1 18

1 6

1 4

1 12

Найти: математические ожидания, дисперсии случайных величин X и Y, коэффициент корреляции.

mx		M ( X ) 1			1	2	1	3		1		1	1	2		1	3		1	1		1	2		1	3		1		7		;
mx		M ( X ) 1				2	9	3		6		1	12	2		6	3		4	1		36	2			3		12		3		;
				18			9			6			12			6			4			36			18			12		3
m		M (Y ) 1			1	2	1		3		1	1		1	2		1	3		1	1		1	2		1	3		1		11
m	y	M (Y ) 1				2			3			1			2			3			1			2			3
	y			18			12				36			9			6			18			6			4			12			6
				18			12				36			9			6			18			6			4			12			6
		7	11
Точка			;		является центром рассеивания для заданной системы (X, Y).
		3	6

Так как случайные величины X и Y независимы, то математические ожидания	m	x
		x
и my можно подсчитать проще, используя ряды распределения:

1	2
1		1
6	3

1 2

y j

p	j

1 3

1 2

1 6

Отсюда находим

mx	pi xi	1	2	3	7	,	my	p j	y j	1	1	1	11
		6	3	2	3					3		2	6

От системы (X, Y) перейдём к системе центрированных величин Составим таблицу

X mx \Y my			5	1
X mx \Y my			5
			6	6
				6

	4	1			1
	3	18		12
	3	18		12
	1	1		1
	1
	3	9		6
		9


2		1		1

3		6		4

( X

m	, Y
x

m	)
y

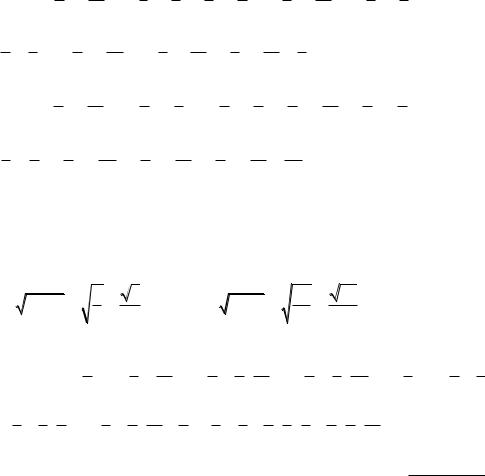
Тогда

					4	2			1				1			2		1				2				2			1				4			2		1			1		2	1
D( X )					4				1				1					1				2							1				4					1			1			1
D( X )
								18										9											6									12			3			6
					3			18					3					9				3							6				3					12			3			6
	2	2	1			4			2		1						1			2		1					2			2		1			5
	2		1			4					1						1					1					2					1			5

			4								36						3				18											12			9
	3		4			3					36						3				18						3					12			9
					5	2			1					5			2		1						5				2		1			1			2		1	1		2		1
D(Y )					5				1					5					1						5						1			1					1	1				1
D(Y )
								18											9												6								12					6
					6			18						6					9						6						6			6					12	6				6
	1	2		1	7			2		1				7			2			1				7				2			1		17
	1			1	7					1				7						1				7							1		17
				4						36									18											12			36
	6			4	6					36				6					18					6						12			36
Заметим, что							D(X )					и			D(Y )								можно найти по формулам:
Заметим, что												и											можно найти по формулам:
			D(X ) M (X 2 ) M (X ) 2 ,																										D(Y ) M (Y 2 ) M (Y ) 2

Средние квадратичные отклонения:

x	D( X )	5	5	,
		9	3

Определим ковариацию:

	D(Y )	17	17
y		36	6

cov( X ,Y

Так как

)		4
		3

1	1
6	6

cov(X ,Y

1		7
		6
3		6

) 0	,

			1		4	1		1				4		7		1			1			5	1
		18
						6		12						6	36								9
					3	6		12				3		6	36				3			6	9
	1			2	5		1		2	1	1		2		7		1	0
																		0
18							6		3	6	4		3		6	12
18				3	6		6		3	6	4		3		6	12
то и коэффициент корреляции																	r				cov( X ,Y )
																	r
																	xy			( X ) (Y )
																				( X ) (Y )

Лекция 7 Тема: Случайные процессы

Случайной функцией X(t) называют функцию неслучайного аргумента t, которая при каждом фиксированном значении аргумента является случайной величиной.

Конкретный вид, принимаемый случайной функцией X(t) в результате опыта, называется реализацией случайной функции.

Сечением случайной функции X(t) называют случайную величину, соответствующую фиксированному значению аргумента случайной функции.

Пример. Самолет на воздушном курсе имеет теоретически постоянную воздушную скорость V. Фактически его скорость колеблется около этого среднего номинального значения и представляет собой случайную функцию времени. Полет можно рассматривать как опыт, в котором случайная функция V(t) принимает определенную реализацию.

На практике встречаются случайные функции, зависящие не от одного аргумента, а от нескольких, например, состояние атмосферы (температура, давление, ветер, осадки). В данном курсе мы будем рассматривать только случайные функции одного аргумента. Так как этим аргументом чаще всего является время, будем обозначать его буквой t. Кроме того, условимся обозначать случайные функции большими буквами (X(t), Y(t), …) в отличие от неслучайных функций (x(t), y(t),

…).

Случайным (стохастическим) процессом

аргумент которой истолковывается как время. Пусть случайная функция X t . В момент t

называют

имеем

случайную

X	1	X t
	1	1

функцию,

с законом

распределения

f	(x	,t	)
1	1	1

. В момент

t t	2

имеем

X	2	X t
	2	2

с законом распределе-

ния

f	(x	,t	2	)
1	2		2

. То есть, имеем одномерную плотность в любой момент времени.

Рассмотрим простейшие характеристики случайных функций, аналогичные числовым характеристикам случайной величины.

В отличие от числовых характеристик случайных величин, представляющих собой числа, характеристики случайных функций представляют собой в общем слу-

чае функции.

Рассмотрим сечение случайной функции X(t) при фиксированном t. Математическим ожиданием случайной функции X(t) называется неслу-

чайная функция mx(t) = M[X(t)], которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.

Свойства математического ожидания случайной функции.

1.Математическое ожидание неслучайной функции φ(t) равно самой неслучайной функции: M[φ(t)] = φ(t).

2.Неслучайный множитель φ(t) можно выносить за знак математического ожида-

ния: M[φ(t) · X(t)] = φ(t) · M[X(t)] = φ(t) · mx(t).

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете Прикладные задачи математической статистики

#
15.03.20251.13 Mб1PZMS.pdf
#
15.03.20256.63 Mб1Лекции.pdf
#
15.03.2025628.43 Кб2Практика 4 (2).pdf
#
15.03.20252.56 Mб1Практика 4.pptx
#
15.03.2025510.69 Кб1Практическая работа № 1. Первичная обработка данных.pdf
#
15.03.2025232.82 Кб1Практическая работа №2 Интервальные оценки параметров.pdf
#
15.03.2025500.35 Кб1Практическая работа №3 Идентификация распределений (2).pdf

X\Y	y1	y2	…	yn
x	p	p	…	p
1	11	12		1n

x2	p21	p22	…	p2n
…	…	…	…	…

xm	pm1	pm2	…	pmn

X\Y	y1	y2	…	yn
x	p	p	…	p
1	11	12		1n

x2	p21	p22	…	p2n
…	…	…	…	…

xm	pm1	pm2	…	pmn

X\Y	y1	y2	…	yn
x	p	p	…	p
1	11	12		1n

x2	p21	p22	…	p2n
…	…	…	…	…

xm	pm1	pm2	…	pmn