Добавил:

ukusezha Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Прикладные задачи математической статистики

Файл:

Лекции

.pdf

Скачиваний:

Добавлен:

15.03.2025

Размер:

6.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

M(X ) xf (x)dx

Дисперсией непрерывной случайной величины Х называется интеграл от произ-

ведения квадрата разности между ее значениями и математическим ожиданием на плотность распределения вероятностей f(x):


D( X ) [x M ( X )]	2	f (x)dx
D( X ) [x M ( X )]		f (x)dx

Для вычислений удобно использовать формулу:


D(X ) x	2	f (x)dx (M (X ))	2
D(X ) x		f (x)dx (M (X ))

Все свойства математического ожидания и дисперсии, указанные выше для дискретных случайных величин, сохраняются и для непрерывных величин.

Среднее квадратическое отклонение непрерывной случайной величины опре-

деляется так же, как и для дискретной величины:

(X )

D(X )

Пример. Случайная величина Х задана функцией распределения

F (x) =

		0	, если х 0
	2	, если 0 x 1
х	2
х
		1	, если х 1
		1	, если х 1

Найти: математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).

Решение: Найдем плотность распределения:

f(x)=

F (x)

		0	, если х 0
		2х, если 0 x 1
		2х, если 0 x 1

		0	, если х 1
		0	, если х 1

Найдем математическое ожидание:

1	1	1	x	3	1	2
M ( X ) хf (x)dx x2xdx 2 x2dx 2
			3			3
0	0	0			0

Найдем дисперсию и среднее квадратическое отклонение, учитывая что М(X)

= 3 :

				1													1						2		2	1		4
D( X ) x						2	f (x)dx			(M ( X ))			2				x	2					2			3	dx	4
D( X ) x							f (x)dx			(M ( X ))							x		2xdx							2 x	dx
				0													0						3			0		9
				0													0									0
	x	4		1			4	1		4		1
		4
2
2	4						9	2
	4			0			9	2		9	18
				0

										1		1
( X )					D( X )					1		1
									18
												3	2
												3	2
			Вероятность того, что в результате испытания Х примет значение, принадле-
жащее интервалу (0,5; 1):
									1
P(0,5 X ) 2 xdx x2 1																	1 0, 25 0, 75.
															0,5
									0,5
												5.		Равномерное распределение
			Непрерывная случайная величина																			X		называется распределенной равномерно
на отрезке [а; b], если плотность вероятности задается формулой:
																						0		, если х а,
																						1
																						1		, если a x b,
																f (x)				b		a		, если a x b,
																				b		a
																									, если х b.
																						0			, если х b.

			Функция распределения для равномерно распределенной случайной вели-
чины на отрезке [а; b]:
																						0		, если х а,

																			х a					, если a x b,
															F ( X )						b a			, если a x b,
																					b a
																									, если х b.
																						1			, если х b.

Числовые характеристики данной случайной величины вычисляются по фор-

мулам:

M ( X )

a b 2

	(b a)	2
D( X )
	12

( X )	D( X )	b a
		2	3

Вероятность попадания равномерно распределенной случайной величины Х в интервал (α, β), расположенный внутри отрезка [a, b]:

	1		x
P( X ) f (x)dx		dx
	b a		b a

b a

6. Показательное (экспоненциальное) распределение

Непрерывная случайная величина		X	называется распределенной по показа-
		X
тельному закону, если её плотность вероятности имеет вид:
0	при x 0,
f (x)
e x при x 0,

где некоторый положительный постоянный параметр.

Функция распределения (интегральная функция) показательного закона:

0	при	x 0,
F(x)	e x при x 0
1	e x при x 0

Вероятность попадания случайной величины Х в интервал (α, β):

Р(α <X< β) = F(β) - F(α) = (1-e-λβ) -(1-e-λα) = e-λα - e-λβ,

то есть Р(α <X< β) = e-λα - e-λβ.

Числовые характеристики данной случайной величины вычисляются по фор-

мулам: M ( X ) 1 ,

D( X )	1
D( X )
	2

	(Х)	1
	(Х)

Если Т – непрерывная случайная величина, выражающая продолжительность времени безотказной работы какого-либо элемента, а λ - интенсивность отказов (среднее число отказов в единицу времени), то продолжительность времени t безотказной работы этого элемента можно считать случайной величиной, распределенной по показательному закону с функцией распределения

F(t)=P(T<t)=1- e-λt (λ>0),

которая определяет вероятность отказа элемента за время t .

Функция надежности R(t) определяет вероятность безотказной работы элемента за время t: R(t)=e-λt.

Пример. Для какого значения k функция


0	при		x 0,
f (x)	x	при x 0
k e		при x 0

является функцией плотности показательного закона?

Решение:

Так как f(x)=0 при x<0, то

f (x)dx ke

dx 1

Отсюда,

dx k

, то есть k = λ.

Пример. Непрерывная случайная величина Х распределена по показательному закону:


0		при x 0,
f (x)	4 e 4 x при x 0.
	4 e 4 x при x 0.

Найти вероятность того, что в результате испытаний Х попадет в интервал

(0,2; 0,5).

Решение: Используя формулу Р(α <X< β) = e-λα - e-λβ, получим

Р(0,2 <X< 0,5) = е-0,8-е-2 = 0,4493 - 0,1353 = 0,314.

7. Нормальное распределение

Непрерывная случайная величина X называется распределенной по нормальному закону, если её плотность вероятности имеет вид:

			( x a)		2
	1		( x a)
f (x)	1		2	2
		e	2
	2	e
	2

( 0),

где

a M (X ),

(X )

Функция распределения нормального распределения имеет вид:

F(x)	1
F(x)
	2

При а=0, σ =1

	(t a)		2
	(t a)
	2	2
e		2	dt


			.

получаем стандартное нормальное распределение с функцией

				х	2
		1		х
плотности распределения вероятностей	(х)	1	е	2		.
	(х)		е

		2
		2

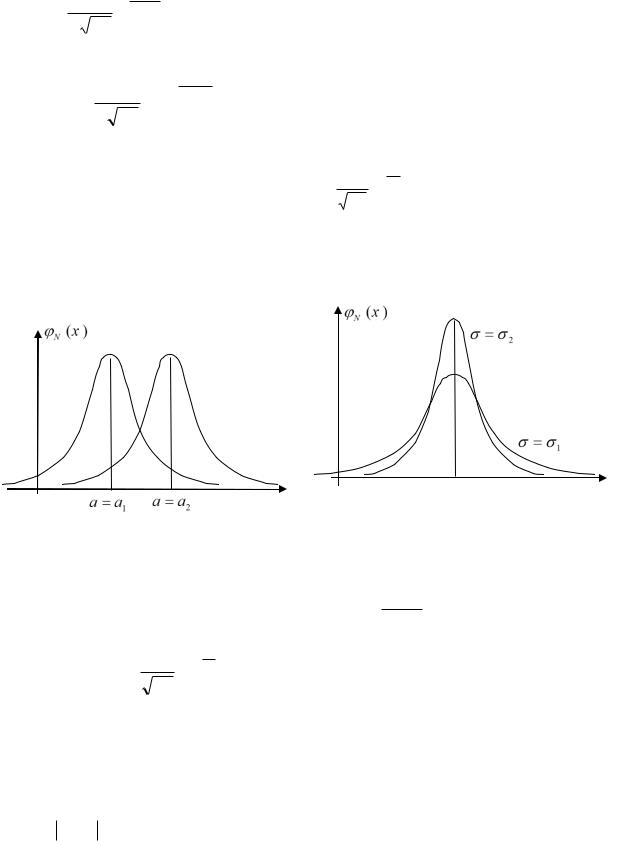
Отметим, что график N (x ) – результат деформации Гауссовой кривой. Рас-

смотрим, как изменяется этот график при изменении параметров а и закона.

нормального

x	а	x
x

Для нормально распределенной случайной величины вероятность её попадания в заданный промежуток вычисляется по формуле:

где

P( X )
				t	2
	1	х		t
Ф(х)	1		е			dt

				2
				2
	2 0

	a		a
F ( ) F ( ) Ф		Ф

- функция Лапласа.

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X от её среднего значения по абсолютной величине меньше заданного положительного , то есть вычислить вероятность

неравенства X a :


P( X a ) 2Ф		.

Тогда справедливо «правило трех сигм»: практически достоверно, что нормально распределенная величина попадет в интервал радиусом 3 с центром в точке а:

P( X a 3 ) P(a 3 X a 3 ) 2Ф(3) 0,9973						.
						.
Пример. Плотность вероятности нормально распределенной случайной вели-
чины задана формулой:
	1			(x 5)2
f (x)	1		e	32	.
				32

		2
4
4

Найти её математическое ожидание и дисперсию.

Решение:

Если сравнить данную по условию формулу с общей формулой плотности вероятности нормального распределения, то можно заметить, что в данном случае

a 5, 4	.
	.
Таким образом,		M(X) a 5,	D(X)	2	16	.
		M(X) a 5,	D(X)		16

Пример. Математическое ожидание и дисперсия нормально распределенной случайной величины X соответственно равны 30 и 100. Найти вероятность того, что данная случайная величина попадет в интервал (10; 50).

Решение:

Воспользуемся формулой нахождения вероятности для нормально распределенной случайной величины.

В данном случае

a 30,

10,

, следовательно,

50 30		10 30		2Ф(2)	2 0,47725 0,9545.
P(10 X 50) Ф		Ф		2Ф(2)	2 0,47725 0,9545.
	10		10

Лекция 6 Тема: Начальные и центральные теоретические моменты.

Операции над случайными величинами. Закон больших чисел. Двумерные случайные величины. Ковариация и коэффициент корреляции.

1. Начальные и центральные моменты. Асимметрия и эксцесс случайной величины.

Ранее нами были рассмотрены важнейшие числовые характеристики случайных величин: математическое ожидание как одна из числовых характеристик центра группирования и дисперсия как одна из характеристик вариации значений случайной величины. Однако эти две характеристики хотя и являются самыми важными, но далеко не исчерпывают всего набора употребляемых числовых характеристик случайной величины. Рассмотрим начальные и центральные моменты, а также асимметрию и эксцесс случайной величины.

Начальным моментом k-го порядка, который обозначается как νk, называется математическое ожидание k-й степени случайной величины:

νk = М(Хk), k=1,2,3,…

Например, первый начальный момент – это обычное математическое ожидание: ν1 = М(Х). При небольших допущениях относительно случайной величины можно доказать, что значение всех ее начальных моментов позволяет восстановить ее функцию распределения как обобщающую характеристику случайной величины. Например, если известны математическое ожидание и дисперсия нормальной случайной величины: а = ν1, σ2 = ν2-ν12 то известна и ее функция плотности (а следовательно, и функция распределения), поэтому нормальная случайная величина полностью определяется первыми двумя начальными моментами.

Центральным моментом k-го порядка, который обозначается как μk, называ-

ется математическое ожидание k-й степени отклонения случайной величины от своего математического ожидания:

μk= М(Х-М(Х))k.

Центральный момент первого порядка равен нулю: μ1= М(Х-М(Х))=0. Второй центральный момент – это дисперсия: μ2= М(Х-М(Х))2=D(Х) Любой центральный момент можно выразить через начальные:

μ2 = ν2-ν12;
μ3	= ν3-3ν1ν2+2ν13;
μ4	= ν4-4ν1ν3+6ν	1	ν2-3ν
		2

4 1

Отношение центрального момента третьего порядка к кубу среднего квадра-

тического отклонения называется асимметрией:

S	k

3 3 х

Асимметрия является характеристикой «скошенности» кривой распределе-

ния.

Эксцессом случайной величины Х называется величина	E		4	3
	E			3

		x	4
			х
			х

Эксцессэто характеристика «островершинности» кривой распределения. Пример. Дан ряд распределения случайной величины Х:

Х	1	3	5	7	9

Р	0,1	0,4	0,2	0,2	0,1

Найти начальные и центральные моменты первых четырех порядков этой случайной величины, а также определить асимметрию и эксцесс.

Решение:

Начальный момент первого порядка:

	1	1 0,1 3 0, 4 5 0, 2 7 0, 2 9 0,1 4, 6	.

Начальный момент первого порядка является математическим ожиданием, поэтому М(Х) = 4,6.

Найдем начальный момент второго порядка:



1 0,1 9 0, 4 25 0, 2 49 0, 2 81 0,1 26,6
Начальный момент третьего порядка:
1 0,1 27 0, 4 125 0, 2 343 0, 2 729 0,1 177, 4	.
	.
Начальный момент четвертого порядка:

	4

1 0,1 81 0, 4 625 0, 2 2401 0, 2 6561 0,1 1293,8

Найдем теперь центральные моменты. Как известно, μ1=0. Центральный момент второго порядка найдем по формуле:

μ2= ν2-ν12=26,6-(4,6)2=26,6-21,16=5,44.

Этот центральный момент является дисперсией случайной величины, то есть

D(X) = 5,44.

Тогда среднее квадратическое отклонение:

(X )

D(X )

5, 44 2,33

Центральный момент третьего порядка определится по формуле: μ3 = ν3-3ν1ν2+2ν13 = 177,4-3ּ4,6ּ26,6+2ּ(4,6)3 =177,4-367,08+194,672 = 4,992.

Определим асимметрию:	S		3		4, 992		4, 992	0, 394
		k		3	5, 44 2, 33	12, 675

				х

Для центрального момента четвертого порядка воспользуемся формулой:

μ4 = ν4-4ν1ν3+6ν12 ν2-3ν 14 =1293,8-4ּ4,6ּ177,4+6ּ(4,6)2ּ26,6-3ּ(4,6)4= =1293,8-3264,16+3377,136-1343,2368 = 63,5392.

E	x

Теперь можно найти эксцесс:

4	3	63, 5392		3	63, 5392	3
	3			3		3

4		(5, 44)	2		29, 5936
х		(5, 44)			29, 5936
х

2,15 3

0,85

Пример. Случайная величина Х задана плотностью распределения f(x)=2х в интервале (0,1); вне этого интервала f(x)=0. Найти начальные моменты первого и второго порядка.

Решение: По формуле

k M(x	k	1	k
	k	) x	k	f (x)dx
		) x		f (x)dx
		0

найдем начальные мо-

менты первого и второго порядков:

1	1			x	3
		2
1 x (2x)dx 2 х			dx 2
				3
0	0

2 3

;

	1	2	1			x	4	1
		2					4
				3
2	x		(2x)dx 2 х	3	dx 2
2	x		(2x)dx 2 х		dx 2	4
	0		0			4		0
								0

1 .

2. Операции над случайными величинами

Определение. Случайные величины Х и Y называются равными, если их законы распределения точно совпадают, и для произвольного числа справедливо ра-

венство: (X

) (Y

Пример. Пусть законы распределения случайных величин Х и Y имеют вид:

x i

y i

p i

0,5

p i

0,5

Эти случайные величины равны, если дополнительно справедливы равенства

(X 0) (Y

0) и

(X 1)

1) , т.е. случайная величина Х принимает зна-

чение 0 тогда и только тогда, когда случайная величина Y принимает значение 0, и

аналогично со значением 1.

Произвольная случайная величина допускает умножение на число. Действи-

тельно, пусть закон распределения случайной величины Х имеет вид:

X :

x i

x 1

x 2

…

x k

p i

p 2

…

p k

и – некоторое число.

Определение. Случайной величиной Y X

называется такая случайная

величина, закон распределения которой имеет вид :

:	y i	x 1	x 2	…	x k

	p i	p 2	p 2	…	p k

Пример. Пусть закон распределения случайной величины Х имеет вид:

	Х :	x i		0	1	2

		p	i	0,16	0,48	0,36
			i	0,16	0,48	0,36
и 5 , Y X .
и 5 , Y X .
Тогда закон распределения Y :

	Y :	y i		0	5	10

		p i		0,16	0,48	0,36

Определение. Случайные величины Х и Y называются независимыми, если
для любых i и j события	(X x i	) и (Y		y j ) – независимы.

Пример. Пусть из коробки, в которой – 6 белых и 8 красных шаров, извлекается 1 шар. Рассмотрим случайные величины Х – число белых шаров, Y – число

красных шаров из извлеченных. События, например, (X

и (Y

– несовместны

и зависимы. Следовательно, и случайные величины Х и Y зависимы.

Определение. Суммой (разностью, произведением) случайных величин Х и

Y называется такая случайная величина

Z X Y

( Z X Y

, Z X

), которая

принимает значение

z k

в некотором испытании,

если значения x i и

y j

случайных

величин Х и Y

в этом испытании таковы, что

(

, z

j ).

Пример. Пусть заданы законы распределения независимых случайных вели-

чин Х и Y:

Х:

Y :

x i

y j

0,4

0,6

0,2

0,8

Составить закон распределения случайной величины

U X Y .

Решение. Удобно использовать вспомогательную таблицу вида:

y	j

x	i

в каждой из центральных клеток которой случайных величин X и Y.

U 0 тогда и только тогда, когда

0	1
0	1
–1	0

записаны соответствующие произведения

X 0 и Y 0 или X 1 и Y 1.

Поэтому

P (U 0) P ((X

0)(Y

0) (X

1)(Y

1))

Применяя рему умножения величины X и Y

теорему сложения вероятностей для несовместных событий, теовероятностей – для независимых событий (по условию, случайные

– независимы), получаем

P (U 0) P (X

0)P (Y

0) P (X

1)P (Y

1) 0,4 0,2 0,6 0,8 0,56.

Для наступления каждого из двух оставшихся значений случайной величины U (-1 и 1) имеется по одной возможности.

Например,	U	1		тогда и только тогда,

Тогда получаем:			P (U 1) P ((X 1)(Y

когда

0))

P (X

1	и	Y

1)P

0) 0,6 0,2 0,12.

Аналогично,

P (U 1) P ((X

0)(Y

1)) P (X

0)P (Y

1) 0,4 0,8 0,32.

Окончательно, закон распределения случайной величины U имеет вид:

U :	u i		–1	0	1

	p	i	0,32	0,56	0,12
		i	0,32	0,56	0,12

3. Закон больших чисел.

Неравенство Маркова

Если возможные значения случайной величины X неотрицательны и су-

ществует её

M (X )

, то для любого положительного числа ε справедливо нера-

венство Маркова:

P( X )	M ( X )	(1)

Другая форма неравенства Маркова:

P( X ) 1	M ( X )	(2)

Пример. Среднее число молодых специалистов, ежегодно направляемых в аспирантуру, составляет 200 человек. Оценить вероятность того, что в данном году будет направлено в аспирантуру менее 220 молодых специалистов.

Решение:

Случайная величина X - число молодых специалистов, ежегодно направляемых в аспирантуру. По условию M(X)=200, ε = 220.

Применяя неравенство (2), получим:

	P( X ) 1	200
		220

То есть вероятность того, что в данном году направлено в аспирантуру менее 220 молодых специалистов, будет не менее 0,909.

Пример. Оценить вероятность того, что при 3600 независимых подбрасываниях игрального кубика число появлений 6 очков будет не менее 900.

Решение:

Пусть случайная величина X - число появлений 6 очков при 3600 подбрасы-

ваниях игрального кубика. Тогда

	M ( X ) 3600	1
	M ( X ) 3600	6
		6

600

, ε = 900.

По формуле (1) получим:	P( X 900)	600
	P( X 900)	900


То есть вероятность того, что при 3600 независимых подбрасываниях иг-
рального кубика число появлений 6 очков не менее 900, будет не более			.

Неравенство Чебышева

Если X - случайная величина,	M

бого положительного числа ε справедливо

(X ) a , D(X) – дисперсия, то для лю-

неравенство Чебышева:

P( X a )	D( X )	(3)
P( X a )		(3)
	2

Другой вид неравенства Чебышева:

P( X a ) 1	D( X )	(4)

	2

Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин.

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете Прикладные задачи математической статистики

#
15.03.20251.13 Mб1PZMS.pdf
#
15.03.20256.63 Mб1Лекции.pdf
#
15.03.2025628.43 Кб2Практика 4 (2).pdf
#
15.03.20252.56 Mб1Практика 4.pptx
#
15.03.2025510.69 Кб1Практическая работа № 1. Первичная обработка данных.pdf
#
15.03.2025232.82 Кб1Практическая работа №2 Интервальные оценки параметров.pdf
#
15.03.2025500.35 Кб1Практическая работа №3 Идентификация распределений (2).pdf