
Лекции
.pdf
По условию,
|
|
m |
|
0,9981. |
P 0,75 |
|
0,85 |
||
|
|
n |
|
|
p
Данные границы для доли |
m |
n |
симметричны относительно величины |
0,8 |
, поэтому неравенство |
0,75 m |
n 0,85 |
равносильно неравенству |
|
|
m n 0,8 0,05. |
|
Следовательно, вероятность 0,9981 – это та самая вероятность, которая вычис- |
|
ляется по следствию 2 из интегральной теоремы Муавра-Лапласа при |
0,05 , |
p 0,8,
q
0,2
:
|
m |
0,8 |
0,05 |
|
|
0,05 n |
|
0,9981. |
P |
|
|
|
|
|
|||
|
n |
|
|
|
|
0,8 0,2 |
|
|
|
|
|
|
|
|
|
По таблице функции Лапласа найдем такое значение t, что
(t ) 0,9981.
Это значение: t |
3,1. Тогда |
|||||||
0,05 n |
3,1, |
|
|
|||||
|
0,8 0,2 |
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
n 3,1 |
|
0,8 0,2 0,05 и |
|||||
n |
3,12 0,8 0,2 |
|
615,04 616. |
|||||
|
||||||||
0,052 |
|
|
|
|||||
Заметим, что значение n округлено до целых в большую сторону, чтобы обеспечить, как говорят, “запас по вероятности”.
Кроме того, видно, что полученное значение n достаточно велико (более 100), поэтому применение интегральной теоремы Муавра-Лапласа для решения данной задачи было возможно.
Лекция 4 Тема: Случайные величины.
Функция распределения вероятностей случайной величины. Дискретные случайные величины и их числовые характеристики. Законы распределения дискретной случайной величины
1. Случайные величины. Функция распределения случайной величины
Случайной величиной называют величину, которая в результате испытания принимает то или иное значение, причем неизвестно заранее, какое именно.
Функцией распределения называют функцию F(x), определяющую для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х,
т.е. F (x)=Р (Х<x)
Часто вместо термина «функция распределения» используют термин «интеграль-
ная функция распределения».
Функция распределения обладает следующими свойствами:
1. Значения функции распределения принадлежат отрезку [0;1]:
0 F(x) 1 |
. |
|
1. Функция распределения есть неубывающая функция:
F (x |
2 |
) F (x ), если x |
2 |
x |
|
1 |
1 |
Следствие 1. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале:
|
|
|
|
Р(a X b) F(b) F(a). |
||
Следствие 2. |
Вероятность того, что непрерывная случайная величина Х примет |
|||||
одно определенное значение, например х1, равна нулю: |
||||||
Р( Х х ) 0 |
. |
|
|
|
|
|
1 |
|
|
|
|
|
|
2. Если все возможные значения случайной величины Х принадлежат интервалу |
||||||
(a, b), то |
F(x) 0 |
при |
х а; F(x) 1 |
при |
x b. |
|
|
|
|
|
|||
Следствие. Справедливы следующие предельные соотношения: |
||||||
|
|
|
|
lim F(x) 0, lim F(x) 1. |
||
|
|
|
|
x |
x |
|
4. Функция распределения непрерывна слева:
lim F (x) F (x0 ).
x x0 0
2. Дискретные случайные величины, их числовые характеристики.
Дискретной случайной величиной называется такая величина, число возможных значений которой либо конечное, либо бесконечное счетное множество, т.е. множество, элементы которого могут быть занумерованы.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Формы закона распределения могут быть различными. Для дискретной случайной величины его удобно записывать в виде таблицы, называемой рядом распре-
деления:
xi |
x1 |
x2 |
… |
xn |
… |
|
|
|
|
|
|
pi |
p1 |
p2 |
… |
pn |
… |
|
|
|
|
|
|
Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех возможных значений величины Х на соответствующие вероятности:
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
М ( Х ) х р |
х |
2 |
р |
2 |
... х |
п |
р |
п |
|
|
x |
p |
, |
1 1 |
|
|
|
|
|
i |
i |
|
|||||
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
где
п |
|
pi |
1. |
i 1 |
|
Свойства математического ожидания
1)М(С)=С, где С = const
2)М(СХ) =СМ(Х), где С = const
3) М(Х Y) = М(Х) M(Y)
4) М(ХY) = М(Х)·М(Y), где Х и Y – независимые случайные величины.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
D( X ) M ( Х М ( Х )) |
2 |
p |
(x |
M ( X )) |
2 |
p |
(x |
|
M ( X )) |
2 |
|
|||||||
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
2 |
|
|
|
|
|
... p |
|
(x |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
M ( X )) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следует отметить, что |
M X M ( X ) 0 |
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Более удобная формула для нахождения дисперсии:
D(X) M(X |
2 |
) M(X) |
, |
|
M(X |
2 |
) p x |
2 |
p x |
2 |
... p x |
2 |
||
|
|
2 |
|
где |
|
|
|
|
|
|
|
|
n . |
|
|
|
|
|
|
|
|
1 |
1 |
2 |
2 |
|
n |
||
Дисперсия показывает степень рассеяния значений случайной величины отно- |
||||||||||||||
сительно центра, то есть математического ожидания. |
|
|
|
|||||||||||
Величина (X ) |
|
D(X ) , способная ориентировочно охарактеризовать при- |
||||||||||||
мерный размер отклонения X M (X ) , называется средним квадратическим откло- |
||||||||||||||
нением случайной величины. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Свойства дисперсии |
|
|
||||||
1. D(C) = 0, |
где C = const. |
|
|
|
|
|
|
|
||||||
2. D(СX) = С2D(X), |
где C = const. |
|
|
|
|
|
||||||||
3. D(X±Y) = D(X)+D(Y), где X, Y – независимые случайные величины.
Пример. Задан закон распределения дискретной случайной величины Х:
xi |
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
рi |
0,2 |
0,4 |
0,3 |
0,08 |
0,02 |
|
|
|
|
|
|
Найти числовые характеристики величины Х: М(X), D(X), ( X ) . Составить функцию распределения случайной величины Х.
Решение:
|
5 |
|
|
|
|
|
|
|
М ( X ) |
p x |
p x p x |
p x |
p x |
p x |
|
||
|
i |
i |
1 1 |
2 2 |
3 3 |
4 4 |
5 5 |
|
i 1
0 0, 02 1 0, 4 2 0, 3 3 0,8 4 0, 02 1, 32
D( X ) M ( X |
2 |
) |
(M ( X )) |
2 |
|
|
|||||
|
|
|
|
||||||||
M ( X |
2 |
) |
1 0, 4 4 0,3 9 0, 08 16 0, 02 0, 4 1, 2 0, 72 0, 32 2, 64; |
||||||||
|
|||||||||||
D( X ) 2, 64 (1, 32) |
2 |
2, 64 1, 7424 0,8976; |
|||||||||
|
|||||||||||
( X ) |
D( X ) |
0,8976 0,95. |
|
|
|||||||
Найдём функцию распределения вероятностей случайной величины Х. |
|||||||||||
Если |
x 0 , то |
F(x) P( X x) 0 |
; |
|
|||||||
|
|
|
|
|
|
||||||
Если 0 x 1, то |
F(x) P( X x) 0, 2 |
, так как Х может принять значе- |
|||||||||
ние, равное 0 с вероятностью 0,2;
Если
x
2
, то
F (x)
равно вероятности события
X
x
, которое может
быть осуществлено, если Х примет значение 0 с вероятностью 0,2 или 1 с вероятностью 0,4. Так как эти события несовместны, то по теореме сложения вероятностей
F(x) 0, 2 0, 4 0, 6 |
; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, если x 3 , то |
F(x) 0, 2 0, 4 0, 3 0, 9 |
; |
|||||||||
Если |
x 4 , то |
F(x) 0, 2 0, 4 |
0,3 0, 08 0,98 |
; |
|
||||||
|
|
|
|
|
|
|
|||||
Если |
x 4 , то F(x) 1, так как событие |
X 4 |
достоверно и, следова- |
||||||||
|
|||||||||||
тельно, его вероятность равна 1. |
|
|
|
|
|
|
|||||
Итак, функция распределения: |
|
|
|
|
|
|
|||||
|
|
0, |
если х 0, |
|
|
|
|
|
|
||
|
|
0, 2, |
если 0 х 1, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, 6, |
если 1 х 2, |
|
|
|
|
|
|
|||
F ( X ) |
0,9, |
если 2 х 3, |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,98, |
если 3 х 4, |
|
|
|
|
|
|
|||
|
|
1 |
, если х 4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
Пример. Найти математическое ожидание случайной величины Z=2X+3Y+5, если известно, что М (X)=3, М (Y)=5
Решение:
Используя свойства математического ожидания, получим:
М(Z) = М(2X+3Y+5) = М(2X)+М(3Y)+М(5) = 2М(X)+3М(Y)+5 = 2·3+3·5+5=26
Пример. Случайные величины X и Y независимы.
Найти дисперсию и среднее квадратическое отклонение дискретной случайной ве-
личины Z=2X-3Y+1, если известно, что D (X)=1, D (Y)=9.

Решение:
Используя свойства дисперсии, получим:
D(Z)=D(2X-3Y+1)=D(2X)+D(3Y)+D(1)=4D(X)+9D(Y)=4·1+9·9=85.
Тогда среднее квадратическое отклонение (X ) 
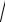 D(X )
D(X ) 
 85 9, 2.
85 9, 2.
Пример. Стрелок стреляет в мишень 3 раза. Вероятность попадания при каждом выстреле равна 0,8. Составить закон распределения случайной величины Х – числа попаданий в мишень.
Решение.
Возможные значения для числа попаданий: 0, 1, 2, 3. Вероятности того, что случайная величина Х примет эти значения вычисляются по формуле Бернулли при
n 3,
p 0,8,
q 0,2 :
P (X |
0) P |
C |
0 |
0 |
3 |
1 1 0,2 |
3 |
0,008, |
|
|
|
|
|
|
|
||||
3 |
p q |
|
|
|
|
|
|
|
|
|
|||||||||
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (X |
1) P |
C |
1 |
|
1 |
2 |
3 0,8 0,2 |
2 |
0,096, |
||||||||
|
|
3 |
p q |
|
|
|
|
||||||||||||
|
|
|
|
|
|
1,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (X |
|
2) P |
C |
2 |
|
2 |
1 |
3 |
0,8 |
2 |
0,2 |
1 |
0,384, |
||||
|
|
|
3 |
p q |
|
|
|
||||||||||||
|
|
|
|
|
|
2,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (X |
|
3) P |
C |
3 |
|
3 |
0 |
1 |
3 |
0,2 |
0 |
0,512. |
|||||
|
|
|
3 |
p q |
|
0,8 |
|
|
|
||||||||||
|
|
|
|
|
|
3,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно искомый закон распределения имеет вид:
Х : |
x i |
|
0 |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
i |
|
0,008 |
|
0,096 |
0,384 |
0,512 |
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
Биномиальное распределение |
|
|
|
|||||
Пусть производятся n независимых испытаний, в каждом из которых, событие |
|||||||||||
A может появиться, либо не появиться. |
|
|
|
|
|
|
|||||
Вероятность наступления события во всех испытаниях постоянна: |
P(A) p . |
||||||||||
Вероятность ненаступления события – q.
Рассмотрим X - число появлений события A в n испытаниях Бернулли.
Дискретная случайная величина X, которая может принимать только целые неотрицательные значения с вероятностью
Р (k) P( X k) Ck |
pk qn k , |
||
n |
|
n |
|
где |
p q 1, |
p 0, q 0, k 0, 1, 2,..., n |
|
|
|
|
|
называется распределенной по биномиальному закону, а p - параметром биномиального распределения.
Для биномиального закона распределения запишем формулы числовых харак-
теристик случайной величины X: |
|
|
математическое ожидание |
M ( X ) np |
; |
|
||
дисперсия |
D( X ) npq |
, где |
q 1 |
|
|
|
|
среднее квадратическое отклонение
p
(X ) 
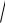 D(X )
D(X ) 
 npq .
npq .
Пример. Найти математическое ожидание и дисперсию числа бракованных деталей среди 40 проверенных, если вероятность того, что деталь стандартна, равна
0,85. |
|
|
Решение: |
|
|
Пусть |
X |
- число бракованных деталей из 40 проверенных. Тогда эта случай- |
ная величина распределена по биномиальному закону, где успехом будет появление
бракованной детали. Таким образом, в данном случае |
n 40, |
p 0,15, q 0,85 |
. |
|
|
Следовательно, |
M (X ) 40 0,15 6, |
D(X ) 40 0,15 0,85 5,1 |
. |
|
|
Пример. Монета брошена 3 раза. Написать в виде таблицы закон распределения случайной величины X – числа выпадений «герба».
Решение:
Вероятность появления «герба»
q 1 p 1 |
1 |
|
1 |
. |
|
2 |
2 |
||||
|
|
||||
|
|
|
р
1 2
, а вероятность не появления «герба»
При трёх бросаниях монеты «герб» может появиться либо 3 раза, либо либо 1 раз, либо совсем не появиться.
Таким образом, возможные значения X: |
x |
3, x |
2, x |
1, x |
0 |
1 |
2 |
3 |
4 |
|
Найдём вероятности этих возможных значений по формуле Бернулли:
2 раза,
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
1 |
|
|
|
|
|
|||
P (3) C |
3 |
|
|
3 |
q |
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
||||||||||||
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
8 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
|
|
3 |
|
||||||
P (2) C |
2 |
|
|
2 |
q 3 |
|
|
|
|
|
|||||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
8 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
2 |
|
3 |
|
|
||||||
P (1) C |
1 |
pq |
2 |
3 |
|
|
|
; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
8 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
1 |
|
|
|
|
||||
P (0) C |
0 |
|
|
|
0 |
q |
3 |
|
|
|
|
|
|
|
|||||||||||||||
|
p |
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
8 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Итак, закон распределения:
X
Р
0
1 8
1 |
2 |
3 |
||
3 |
|
3 |
|
1 |
8 |
8 |
|
8 |
|
|
|
|
|
|
р |
1 |
|
3 |
|
3 |
|
1 |
1 |
|
|
|
|
|||||
i |
8 |
|
8 |
|
8 |
|
8 |
|
|
|
|
|
|
4. Распределение Пуассона
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Если число испытаний велико, а вероятность

р появления события в каждом испытании очень мала, то используют приближенную формулу:
|
|
|
|
|
|
k |
|
|
|
P (k) P( X k) |
|
e |
|
, |
|
|
|||
n |
k ! |
|
|
|
|
|
|
|
где k- число появлений события в n независимых испытаниях, λ = np (среднее число появлений события в n испытаниях),
и говорят, что случайная величина распределена по закону Пуассона с параметром
λ.
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого распределения, то есть
М(х)=np=λ, D(х)=np=λ.
По закону Пуассона распределены, например, число рождения близнецов, число сбоев на автоматической линии, число заявок на обслуживание, поступивших в единицу времени в системах массового обслуживания.
Пример. Среднее число инкассаторов, прибывающих в банк в 15-минутный интервал, равно 2. Прибытие инкассаторов происходит случайным образом и независимо друг от друга. Считая, что случайная величина Х- число инкассаторов, прибывших
в банк за 15 минут, имеет закон распределения Пуассона, найти числовые характеристики случайной величины и вероятность того, что в течение 15 минут в банк прибудет менее трех инкассаторов.
Решение:
По условию математическое ожидание М(Х)=np=λ=2,тогда дисперсия D(Х)=np=λ=2, среднее квадратическое отклонение (Х) = √2.
Вероятность того, что за 15 минут в банк прибудут менее трех инкассаторов будет равна:
Р(Х < 3) = Р(Х = 0) + Р(Х = 1) + Р(Х = 2)
|
|
|
|
|
|
|
|
k |
|
|
|
По формуле Пуассона |
P (k) P(X k) |
|
e |
|
, |
|
|
||||
n |
k! |
|
|
|
|
|
|
|
|
|
получаем: Р(Х=0)=0,1353; Р(Х=1)=0,2707; Р(Х=2)=0,2707.
Тогда Р(Х < 3) = 0,6767
5. Геометрическое распределение
Случайная величина X называется распределенной по геометрическому закону, если она означает число испытаний до первого успеха.
Тогда она принимает бесконечное множество натуральных значений, начиная с 1, вероятности которых определяются по формуле:
P( X n) qn 1 p .
Для такой случайной величины
M ( X ) |
1 |
, |
D( X ) |
q |
||
p |
p |
2 |
||||
|
|
|
||||
|
|
|
|
|||
1 p p 2
.
Пример. Найти математическое ожидание и дисперсию числа проверенных деталей до первого появления брака, если вероятность того, что деталь стандартна,
равна |
8 |
|
9 |
||
|
Решение. Очевидно, что данная случайная величина распределена по геометриче-
скому закону с
p |
1 |
, q |
8 |
|
9 |
9 |
|||
|
|
. Тогда М(Х)=9, D(X)=72.
6. Гипергеометрическое распределение
Пусть из множества в N элементов, в котором есть M отмеченных элементов определённого типа (M < N), случайным образом производится выборка n элементов (без повторов, где n < N).
Если X - число отмеченных элементов в выборке, то формула
|
C |
m |
C |
n m |
|
|
|
|
|
||
Р( X m) |
|
M |
|
|
N M |
|
|
C |
n |
|
|
|
|
|
|
||
|
|
|
N |
|
|
|
|
|
|
|
|
определяет распределение вероятностей, которое называют гипергеометрическим. Математическое ожидание и дисперсия случайной величины Х определяются
формулами:
М(Х) = ; ( ) = (1 − ) (1 − −−11)
Пример. В стопке из 6 книг 3 по математике и 3 по информатике. Выбирают наудачу 3 книги. Составить закон распределения числа книг по математике среди отобранных. Найти математическое ожидание и функцию распределения этой случайной величины.
Решение:
Случайная величина Х- число книг по математике среди 3-х отобранных.
Х может принимать значения 0, 1, 2, 3. Найдем соответствующие вероятности (по формуле гипергеометрической вероятности).
|
|
|
|
|
|
|
С3 |
|
|
|
1 |
|
|||
|
|
|
|
Р(Х = 0) = |
|
3 |
= |
|
|
|
|
||||
|
|
|
|
|
3 |
20 |
|
||||||||
|
|
|
|
|
|
|
С |
|
|
|
|||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
С1 |
С2 |
|
|
9 |
|||||
|
|
|
Р(Х = 1) = |
|
3 |
|
|
3 |
= |
|
|
|
|||
|
|
|
|
|
3 |
|
20 |
||||||||
|
|
|
|
|
|
|
С |
|
|
|
|||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
С2С1 |
|
|
9 |
||||||
|
|
|
Р(Х = 2) = |
|
3 |
|
|
3 |
= |
|
|
|
|||
|
|
|
|
|
3 |
|
20 |
||||||||
|
|
|
|
|
|
|
С |
|
|
|
|||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С3 |
|
|
|
1 |
|
|||
|
|
|
|
Р(Х = 3) = |
|
3 |
= |
|
|
|
|
||||
|
|
|
|
|
3 |
20 |
|
||||||||
|
|
|
|
|
|
|
С |
|
|
|
|||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
Получаем закон распределения: |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
0 |
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi |
1/20 |
9/20 |
9/20 |
|
1/20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Математическое ожидание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
М(Х) |
= |
|
= 3 ∙ |
3 |
= 1,5 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
6 |
||||||||||||||||||||
Найдем функцию распределения, по определению ( ) = ( < ). |
|||||||||||||||||||||||||
Тогда получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
при ≤ 0, ( ) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
при 0 < ≤ 1, |
( ) = 0 + |
1 |
|
= |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
20 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
при 1 < ≤ 2, |
( ) = 0 + |
1 |
|
+ |
9 |
|
= |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
20 |
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
при 2 < ≤ 3, |
( ) = 0 + |
1 |
|
+ |
9 |
|
+ |
9 |
|
= |
19 |
|
|
|
|
|
|
||||||||
20 |
20 |
20 |
20 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
при > 3, ( ) = 0 + |
1 |
+ |
|
9 |
|
+ |
|
9 |
|
+ |
|
1 |
|
= 1 |
|
|
|
|
|
|
|||||
|
20 |
20 |
20 |
|
|
|
|
|
|
||||||||||||||||
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; ≤ 0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
, 0 < ≤ 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
||||
Получили функцию распределения: ( ) = |
|
1 |
, 1 < ≤ 2 |
||||||||||||||||||||||
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
19 |
|
, 2 < ≤ 3 |
|
20 |
||||
|
||||
{ |
|
|
1, > 3 |
|
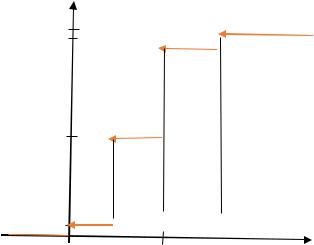
Построим график:
F(x)
1
0,95
0,5
0,05
|
|
|
|
|
x |
0 |
1 |
2 |
3 |
||
Лекция 5 Тема: Непрерывные случайные величины и
их числовые характеристики. Плотность распределения вероятностей. Законы распределения непрерывной случайной величины.
1. Непрерывная случайная величина. Плотность распределения вероятностей.
Случайная величина называется непрерывной, если её значения заполняют некоторый конечный или бесконечный интервал. Функция распределения непрерывной
случайной величины |
F (x) |
непрерывна на всей числовой оси. |
|
|||||
|
|
|
||||||
Дифференциальной |
функцией распределения непрерывной случайной вели- |
|||||||
чины (или плотностью вероятностей), называется функция |
f (x) |
, равная производ- |
||||||
|
||||||||
ной интегральной функции, то есть |
F (x) |
f (x) |
. |
|
|
|||
|
|
|
|
|||||
Свойства плотности вероятностей
1. f (x) 0 для всех x, так как это производная неубывающей функции/
2.
b P(a X b) f (x)dx
a
|
Так как |
F(x) |
- первообразная для |
|
|
|
|||
|
b |
|
|
|
|
f (x)dx F (b) F (a) P(a X |
|||
|
a |
|
|
|
3. |
|
|
|
|
|
f (x)dx 1 |
|
||
|
|
|
||
|
|
|
|
|
f
(x)
b) .
, то по формуле Ньютона-Лейбница:
Пусть
a
и b
, получаем достоверное событие X , вероятность кото-
рого,
4. |
F (x) |
|
Так как
равна единице: |
P( |
|
|
||
x |
|
|
|
f (x)dx |
|
|
|
|
F (x) P( X x) |
||
X
x
f (
)
x)dx
.
|
|
|
f (x)dx |
|
|
1
.
2.Числовые характеристики непрерывных случайных величин
Математическим ожиданием (средним значением, центром распределения)
М(Х) непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
