Теория графов. Лекция 13

Теория графов. Лекция 13

Применение метода ветвей и границ для задачи коммивояжёра

13.1. Постановка задачи. Формальная постановка задачи коммивояжёра приведена в лекции 11. Повторим кратко эту постановку. Пусть задано n точек и известна матрица cij 0 – матрица "расстояний" между точками. Под маршрутом коммивояжёра z в замкнутой задаче будем понимать перестановку i1,i2,…,in точек 1,2,…,n, длина маршрута

Пусть Z – множество всех возможных маршрутов, поскольку начальную точку i1 можно считать фиксированной, то Z =(n–1)!. Требуется найти маршрут z0 Z такой, что

l(z0) = min l(z), z Z.

Опишем основные элементы алгоритма решения задачи, основанного на методе ветвей и границ. (При этом мы следуем в основном работе

[Литл Дж., Мурти К., Суини Д., Кэрел К. Алгоритм для решения задачи коммивояжёра. Экономика и математические методы. 1965 – Т1 – вып.1 –

с. 90-107], уже ставшей классической.)

13.2. Приведение матрицы расстояний. В любой маршрут коммивояжёра входит один элемент каждой строки и каждого столбца матрицы расстояний. Поэтому, если из всех элементов некоторой строки вычесть одно и то же число, то в новой матрице длины всех маршрутов уменьшатся на это число по сравнению со старой матрицей. То же можно сказать и о столбцах матрицы расстояний. Эти свойства объясняются тем, что из каждого города мы должны один раз уйти и в каждый город – один

h j min cij(1) и построим матрицу

i

cij(2) cij(1) hj ,

тогда cij cij(1) ri cij(2) ri hj .

Матрица cij(2) – приведённая матрица расстояний, ri – константы

приведения по строкам, hj – константы приведения по столбцам. Матрица

получим l(z) = l1(z)+d0; т. к. l1(z) , то l(z) d0, т. е. длина любого маршрута оценивается снизу числом d0.

Если после применения процедуры приведения в каждой строке и в каждом столбце ровно один ноль, то мы решили задачу о назначении. Величина целевой функции равна d0, а нули указывают назначение. Если нули образуют единственный цикл, то мы решили задачу о коммивояжёре и длина кратчайшего маршрута равна d0.

Дальнейшее изложение сопровождается примером для n=6 из [Литл,..].

Здесь cii = M – достаточно большое положительное число.

Найдём минимальные элементы по строкам и приведём по строкам:

r1 = 16, r2 = 1, r3 = 0, r4 = 16, r5 = 5, r6 = 5.

Получим матрицу cij(1) :

Найдем минимальные элементы по столбцам и приведём по столбцам:

d0 = 16+1+0+16+5+5+5+5 0=48, l(z) 48.

Для получения верхней оценки в данном примере из первой точки перейдём в ближайшую, затем в ближайшую из оставшихся и т. д.

z1 = {1 4 2 3 6 5 1}, l(z1)=16+16+16+0+5+12=65.

Для оптимального маршрута получим: 48 l(z0) 65.

13.3. Ветвление. Рассмотрим некоторый маршрут, который содержит переход из точки i в точку j. Для длины этого маршрута имеет место неравенство:

Для переходов, у которых c(2) 0 , получаем, что l(z) d . Естественно

ij 0

предположить, что кратчайший путь коммивояжёра содержит один из нулевых переходов.

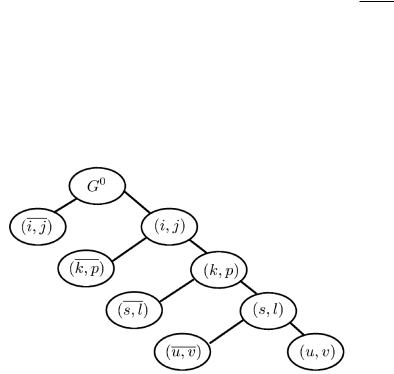
Обозначим через (i,j) множество маршрутов, содержащих переход из i в j непосредственно и через (i, j) – множество маршрутов, не содержащих

множество Z разбивается на два подмножества, см. рис. 13.1. Как известно, ветвление на два подмножества называется дихотомическим.

Рис. 13.1

Рассмотрим нижнюю оценку для множества маршрутов (i, j) . Для (i,j)

оценка остается d0. Для всех маршрутов из (i, j) из точки i нужно уйти в

Поскольку выход из точки i добавляет к оценке по крайней мере наименьший элемент строки i, а вход в точку j – по крайней мере наименьший элемент столбца j, то

Для каждого нулевого перехода может быть вычислена величина

минимальные элементы в строке и столбце, пересекающихся на этом переходе (минимумы находятся без учета рассматриваемого нулевого перехода (i,j)) и полученные минимумы сложить.

В качестве перехода, используемого для разветвления, выбирается

и этот переход выбираем в качестве того, по которому происходит разветвление. Это связано с тем, чтобы получить по возможности большую оценку для множества (i, j) . В нашем примере получаем:

получаем: l(z) 48+10=58, для z (1,4) оценка остается прежней: l(z) 48, см.

рис. 13.2.

Рис. 13.2

В матрице, соответствующей множеству G11 (i, j) , вычёркиваем строку i и столбец j и положим c(ji2) M , чтобы предотвратить появление

цикла i j i. Полученную матрицу можно привести, если сумма констант приведения равна 0, то для z (i,j) получим:

В нашем примере (i,j)=(1,4), поэтому в матрице, соответствующей множеству (1,4), вычеркиваем строку 1 и столбец 4 и полагаем с41=М. После этого выполняем процедуру приведения, 0=1, l(z) 48+1=49. В матрице,

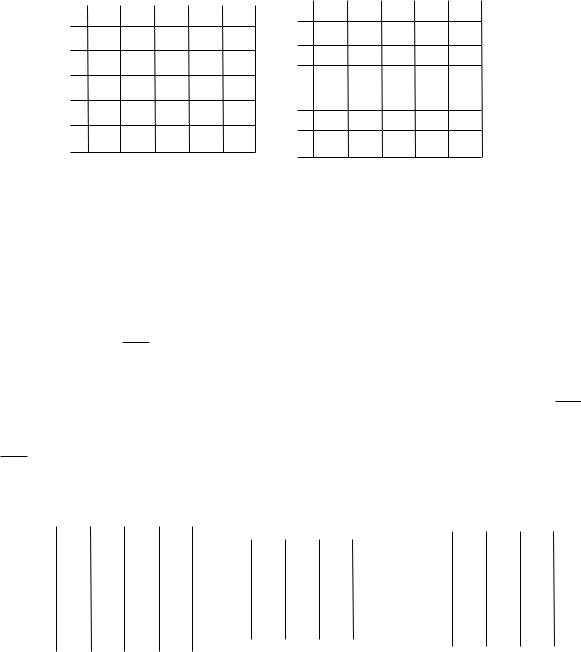
выполнения процедуры приведения 0=10 и l(z) 58+10=68. В данном примере в соответствии с правилами отсева множество (1,4) можно отбросить, т. е. исключить из дальнейшего рассмотрения. Это означает, что в оптимальном решении задачи обязательно содержится переход (1,4). После реализации отсева получим дерево ветвления в следующем виде (см.

рис. 13.3).

Рис. 13.3

13.4. Общий шаг алгоритма. Среди неотсеянных по правилам отсева

и столбец p и реализуем алгоритм запрещения подциклов. Нужно

3)Модифицируем список множеств, не подвергавшихся

отмечаем) множества, отсеянные по правилам отсева и переходим к п. 1, положив t равным t+1.

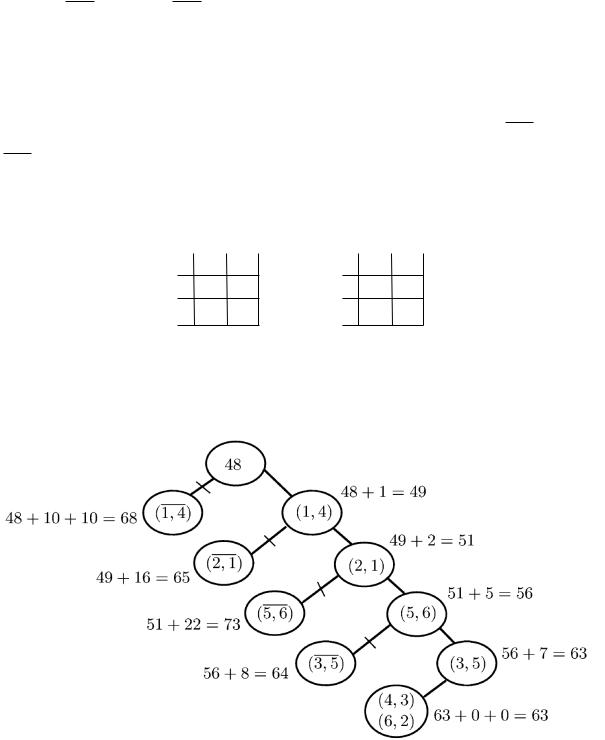
В результате применения описанного общего шага получаем дерево ветвления в следующем виде (см. рис. 13.4):

Рис. 13.4

Здесь описаны правила ветвления и вычисления оценок. Все остальные элементы алгоритма реализуются по общей схеме. Процесс вычисления завершается после отсева по правилам отсева всех множеств, не подвергавшихся разбиению.

Трудоемкость алгоритма определяется числом решённых оценочных задач. В описанном алгоритме решение оценочной задачи сводится к процедуре приведения матрицы расстояний. Экономная её реализация может существенно сократить время решения задачи.

Остановимся на некоторых простых правилах, позволяющих уменьшить время работы процедуры.

1.При определении очередного значения константы приведения

вычитание её из элементов строки или столбца производится, если

константа положительная и её прибавление к оценке не приводит к отсеву подзадачи. Если прибавление положительной константы приводит к отсеву подзадачи, то выполнение процедуры приведения прекращается.

2. Реализация процедуры приведения целесообразно начинать со строк (или столбцов), в которых появились числа М при ветвлении подзадачи на две. Появление чисел М в строках или столбцах, как правило, даёт ненулевые значения констант приведения, при этом увеличиваются значения оценок.

Пример. Завершим решение примера. Удалив в матрице множества

соответствии с (13.2) получаем l(z) 49+16=65, это означает, что множество (2,1) исключаем из дальнейшего рассмотрения. В матрице множества (2,1) удаляем вторую строку и первый столбец, получим:

отсеять. Для z (5,6) удаляем пятую строку и шестой столбец и полагаем

множества (3,5) реализуем запрет подцикла в связном пути (3,5,6), полагая

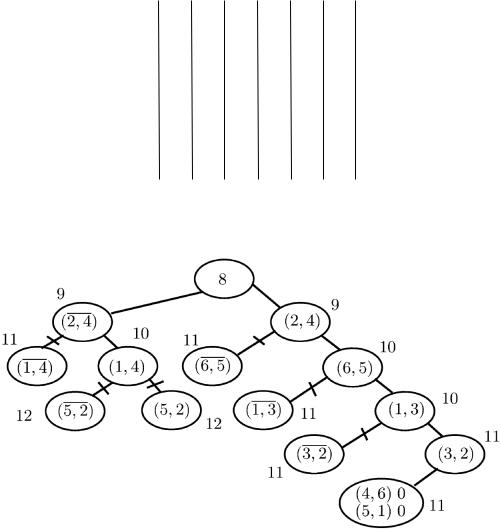
матрицы 2 2 получаем два перехода с нулевой длиной: (6,2) и (4,3). Дерево ветвления с оценками имеет следующий вид (см. рис. 13.5).

Рис. 13.5

После получения нулевых переходов конструируем маршрут z0=(1,4,3,5,6,2,1), l(z0)=63 и вершина с оценкой 64 отбрасывается. Задача решена. Для её решения выполнено пять ветвлений и решено десять оценочных подзадач.

В данном примере на всех шагах подвергалось ветвлению правое на дереве ветвления множество из двух, полученных на данном шаге, при этом получено оптимальное решение. Такое правило ветвления есть

одностороннее ветвление, оно получило название "идите вправо".

Одностороннее ветвление предполагает выбор для ветвления "правого" множества из полученных на данном шаге. При невозможности такого выбора поднимаемся по дереву на предыдущий "этаж", и снова реализуем одностороннее ветвление. Одностороннее ветвление не гарантирует получение оптимального решения при одном проходе, но гарантирует получение рекорда, как правило, близкого к оптимальному решению. Последнее утверждение не может быть строго доказано, оно следует из анализа результатов многочисленных вычислительных экспериментов.

Оптимальное решение z0=(1,3,2,4,6,5,1), l(z0) = 11. Дерево ветвления представлено на рис. 13.6.

Рис. 13.6

Из анализа дерева видно, что после получения вершины (6,5) с оценкой 10 необходимо вернуться к вершине (2,4) с оценкой 9; после получения вершины (1,4) с оценкой 10 возвращаемся к вершине (6,5) и, произведя ветвление, получаем вершину (1,3), а затем вершину (3,2) с оценкой 11 и снова возвращаемся к вершине (1,4). Получив вершины (5,2) и (5,2) с оценками 12, возвращаемся к вершине (3,2), и дойдя до вершин (4,6)

и(5,1) с длиной маршрута l(z0) = 11, завершаем процесс.

Вданном примере правило "идите вправо" также даёт оптимальное решение, но после получения множества с оценкой, равной 11, необходимо

вернуться к множеству (2,4) с оценкой 9 и выполнить ещё два ветвления. Вычислительный опыт показывает, что при решении симметричных

задач возникают большие трудности, которые связаны с тем, что дерево ветвления имеет большое число вершин. Для симметричных задач разработан другой алгоритм, который будет рассмотрен далее.

13.7. Замечание о приведении матрицы расстояний. Существуют два способа приведения матриц расстояний.

1)Сначала приведение по строкам, а затем по столбцам.

2)Сначала приведение по столбцам, а затем по строкам. Результат может быть различный: получаем как разные матрицы, так

иразличные суммы констант приведения. Если n=2, то результат не зависит от способа приведения. Если n>2, то для симметричных матриц результат также не зависит от порядка приведения.

Приведём пример матрицы, для которой результат зависит от способа приведения:

cij P во всех остальных случаях.