Постоянное магнитное поле. Магнетики
2.225.
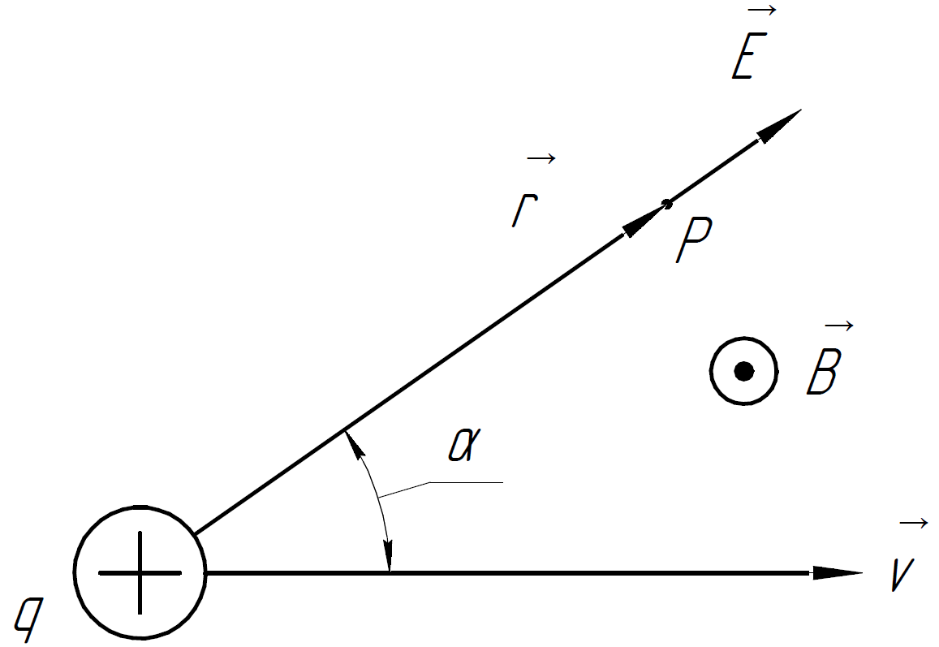
Точечный заряд движется со скоростью
.
В некоторый момент в точке
напряжённость поля этого заряда
,
а между векторами
и
угол
.
Найти индукцию магнитного поля в точке
в данный момент.
Решение.
Пусть
.
Напряжённость электрического поля, создаваемая точечным зарядом на расстоянии :
Движущаяся заряженная частица также создаёт вокруг себя магнитное поле. Согласно закону Био-Савара-Лапласа его индукцию можно найти как:
Или для модуля магнитной индукции:
Так как заряд и расстояние до точки не заданы, то избавимся от них в (3) с помощью (1):
Окончательно получаем:
Ответ:
.
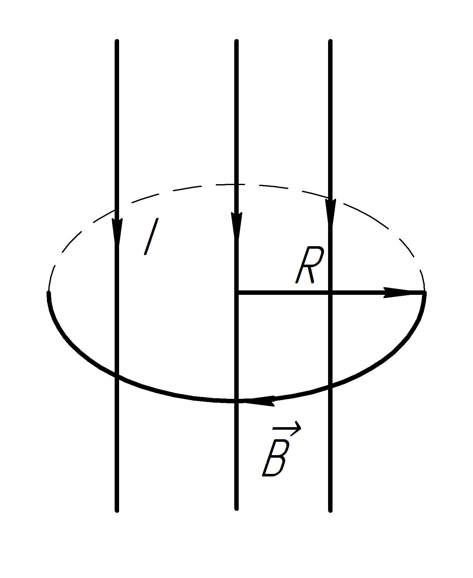
2.226. По
круговому витку радиуса R
=100 мм из тонкого провода циркулирует
ток
= 1,00 А. Найти магнитную индукцию:
а) в центре витка;
б) на оси витка на расстоянии =100 мм от его центра.
Решение.
а) Произвольно выбираем направление тока и по правилу правого винта определяем направление вектора магнитной индукции.
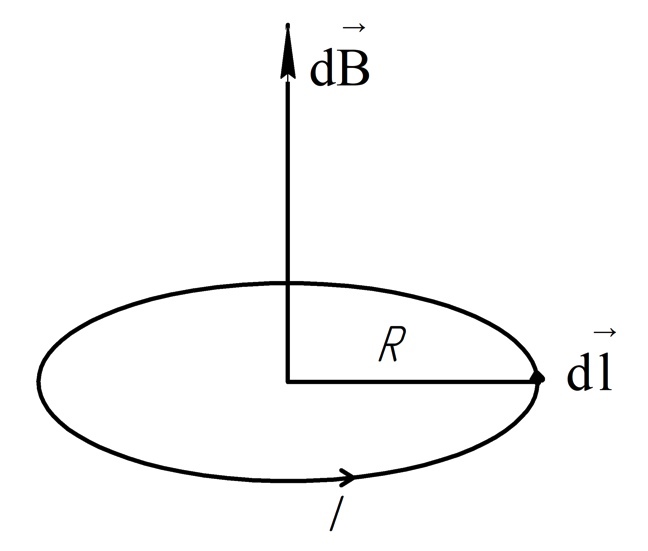
Используем формулу закона Био-Савара-Лапласа для кругового витка с током:
б) Будем ориентироваться на уже выбранное направление тока.
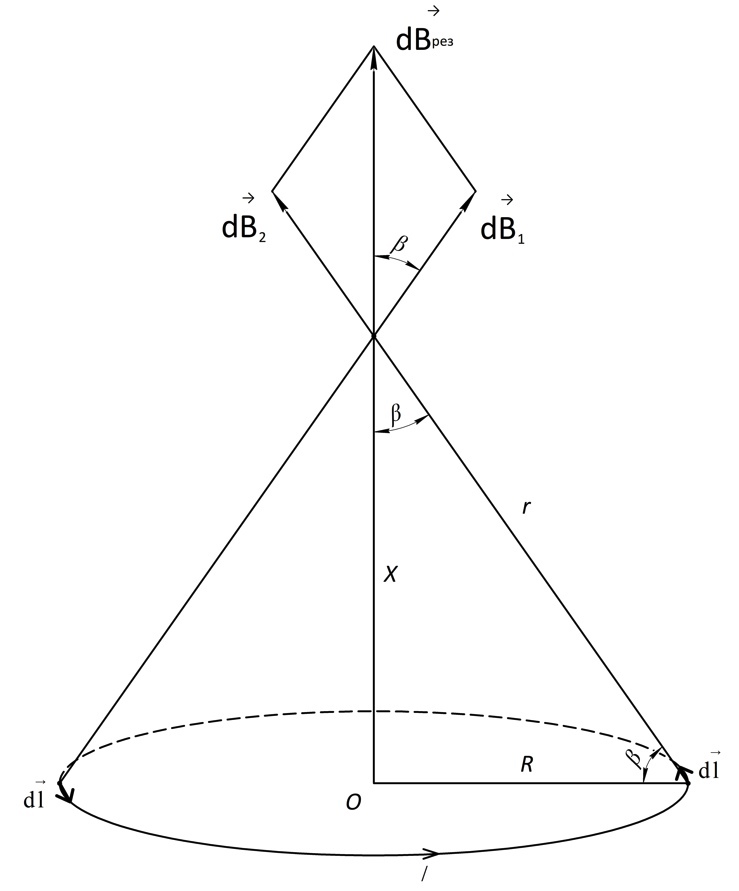Делим
кольцо на бесконечно малые отрезки.
Выбираем 2 симметричные точки (для
упрощения геометрической составляющей
задачи).
Из рисунка видим, что:
Проводим
вектора
.
По принципу суперпозиции определяем
направление результирующего вектора:
направлен вертикально вверх, поэтому
для его нахождения будем суммировать
лишь вертикальные составляющие векторов
:
По закону Био-Савара-Лапласа:
Подставляя числа, получаем:
Ответ: а)
б)
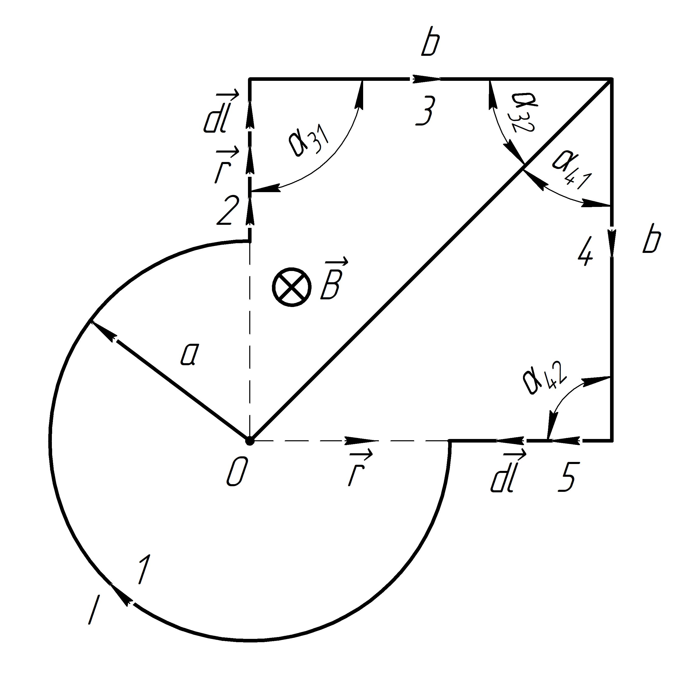
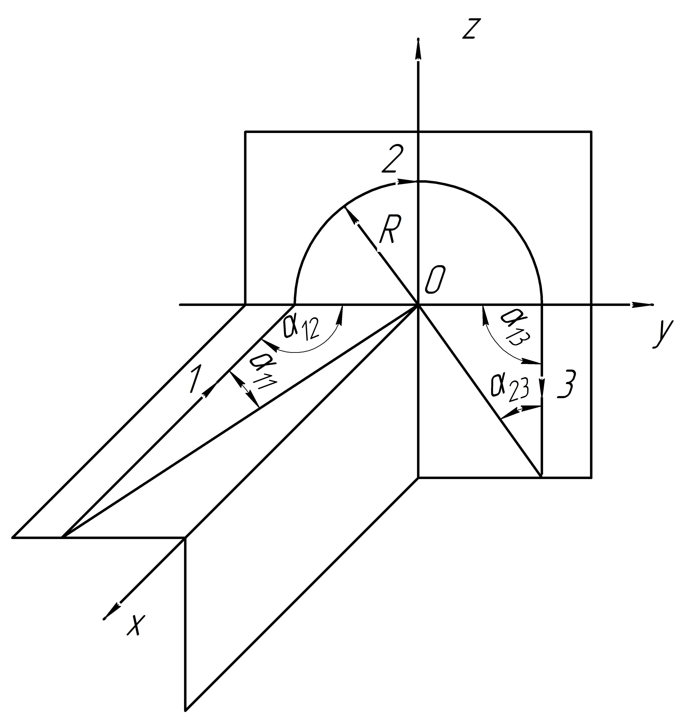
2.232. Найти индукцию магнитного поля в точке контура с током , который показан:
a) на рис. 1; радиусы и , а также угол известны;
б) на рис. 2; радиус и сторона известны.
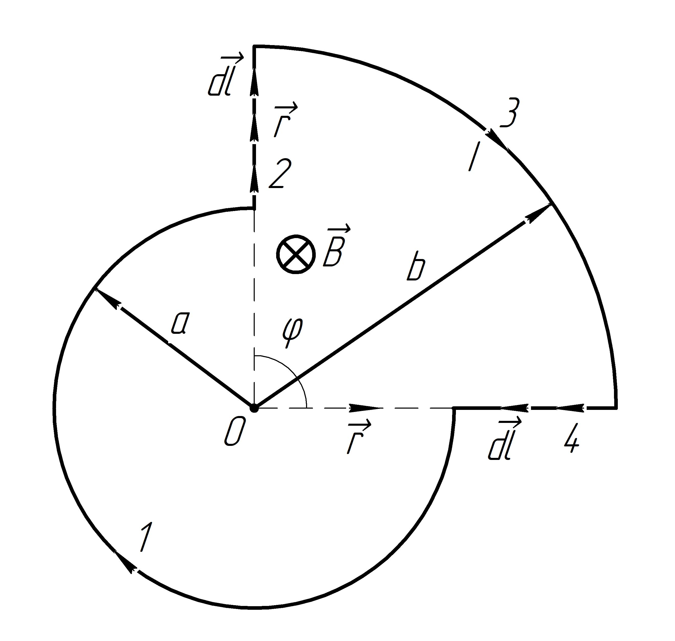Решение.
а) Для начала необходимо разделить
контур на участки, как показано на
рисунке (Рис.1.):
Согласно принципу суперпозиции для вектора магнитной индукции:
Участок 1: используем закон Био-Савара-Лапласа для кругового проводника
Определим
направление
по правилу правого винта: вектор направлен
от нас.
Участки 2 и 4:
угол между
и
равен 0, следовательно
и
.
угол между
и
равен
,
следовательно
и
.
Участок
:
используем закон Био-Савара-Лапласа
для кругового проводника. По правилу
правого винта
направлен от нас.
Угловой размер данного участка:
По закону Био-Савара-Лапласа:
Так как и сонаправлены, то:
Ответ:
б) Для начала необходимо разделить контур на участки:
Согласно принципу суперпозиции:
Участок 1: используем закон Био-Савара-Лапласа для кругового проводника:
Определим
направление
по правилу правого винта вектор направлен
от нас.
Участки 2 и 5:
угол между и равен 0, следовательно и .
угол между
и
равен
,
следовательно
и
.
Участок
:
используем закон Био-Савара-Лапласа
для поля отрезка прямого тока (
).
Рис. 2.
По
правилу правого винта определяем, что
вектор направлен от нас.
Участок 4:
используем закон Био-Савара-Лапласа
для поля отрезка прямого тока (
).
По правилу правого винта вектор направлен от нас.
Таким образом:
Ответ:
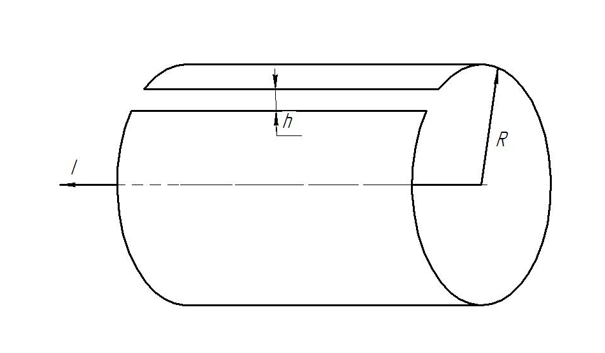
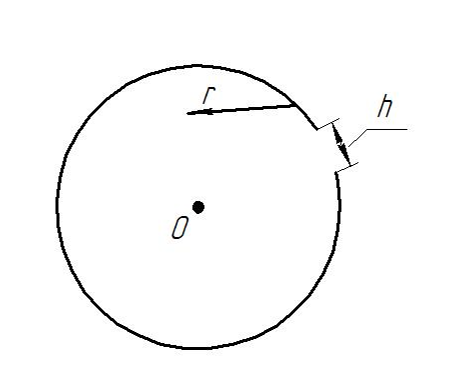
2.233. Ток
течёт вдоль длинной тонкостенной трубы
радиуса
,
имеющей по всей длине продольную проредь
ширины
.
Найти индукцию магнитного поля внутри
трубы, если
.
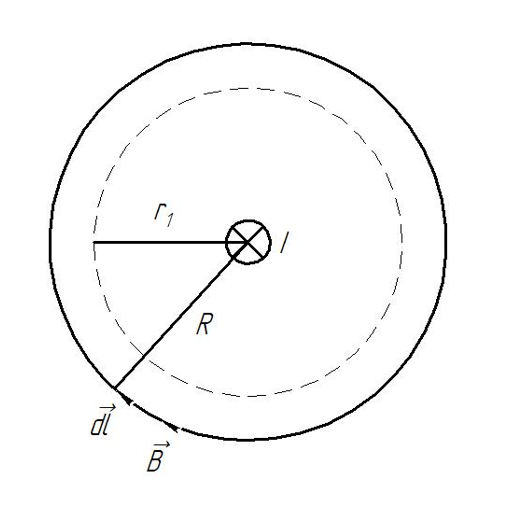
Решение.
Для начала рассмотрим сплошную трубу
без прорези.
Предположим, что по трубе протекает ток , имеющий плотность:
Ток
,
допустим, течет от нас. Тогда по правилу
правого винта вектор магнитной индукции
направлен вдоль силовой линии (окружности)
по часовой стрелке.
Рассмотрим индукцию внутри трубы.
Внутри сплошной трубы индукция магнитного поля равна нулю. Это легко доказать с помощью теоремы о циркуляции вектора магнитной индукции по произвольному замкнутому контуру:
Направление
обхода контура выберем сонаправленное
с вектором
.
Тогда:
так как
– контур радиуса
токов не охватывает.
Теперь найдём магнитную индукцию снаружи сплошной трубы:
В условии задачи речь идет о трубе с прорезью, т.е. в прорези ток равен нулю (плотность тока, соответственно тоже равна нулю).
Для получения
в этой прорези, мы можем рассматривать
эту прорезь как наложение полости с
плотностью тока
на сплошную трубу с плотностью тока
.
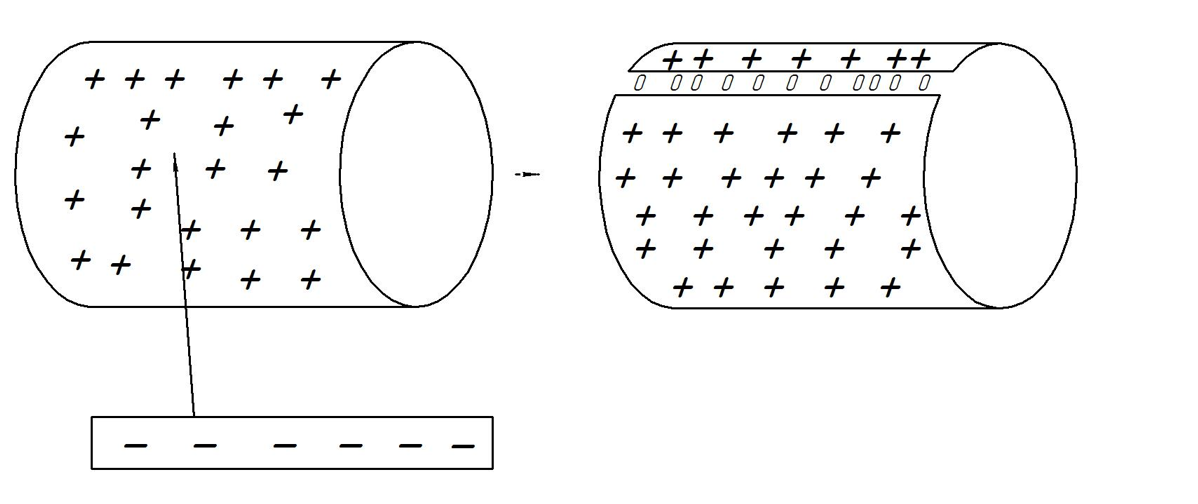В
прорези линейная плотность тока будет
,
по всей трубе
.
Таким образом мы как бы «накладываем»
полоску с отрицательной плотностью
тока на сплошную трубу с положительной
плотностью тока, и в прорези получается
ноль.
Таким образом результирующая плотность тока в прорези:
Магнитная индукция внутри трубы с прорезью будет складываться из индукции магнитного поля внутри сплошной трубы и магнитной индукции, образовавшейся из-за прорези (наложения полоски отрицательной плотности тока).
Индукция магнитного поля прорези вычисляется по закону Био-Савара-Лапласа, точнее по его частному случаю – индукция магнитного поля бесконечно прямого тока:
где
-
ток (отрицательный), текущий через
прорезь.
Однако по условию , поэтому в знаменателе мы можем убрать (оно пренебрежимо мало в сравнении с ).
И тогда
Ответ:
.
2.234 Ток
течет по длинному прямому проводнику,
сечения которого имеет форму тонкого
полукольца радиуса
.
Найти магнитную индукцию на оси
.
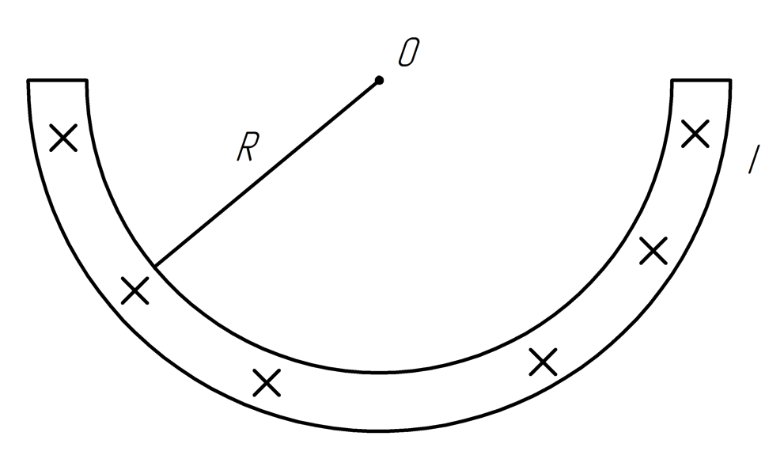Решение.
Допустим, ток направлен от нас.
Разобьем
весь проводник на элементарные нити с
током
и шириной
.
Согласно
правилу правого винта, индукция магнитного
поля каждой из элементарных нитей будет
направлена по часовой стрелке (
)
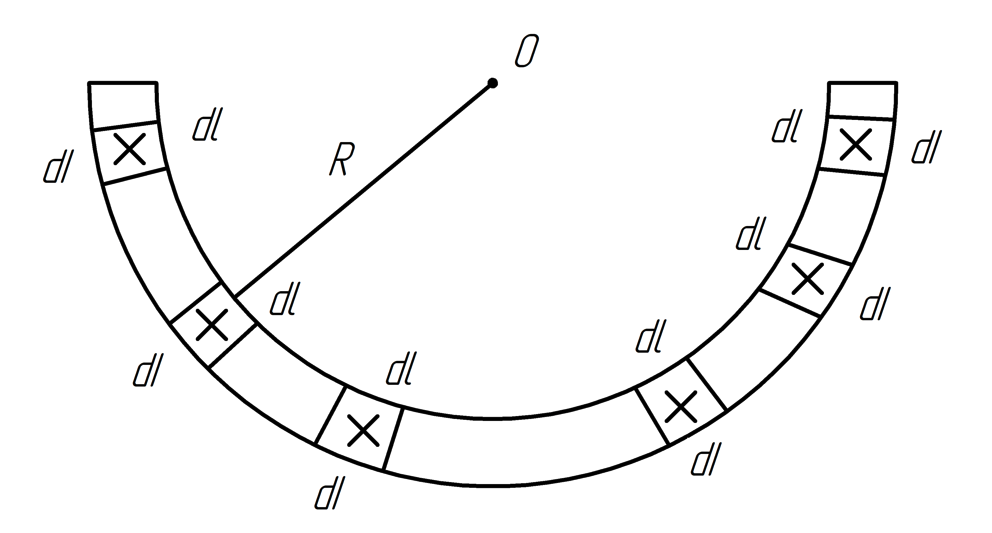Следовательно
вектор
(сумма всех
)
направлен вправо.
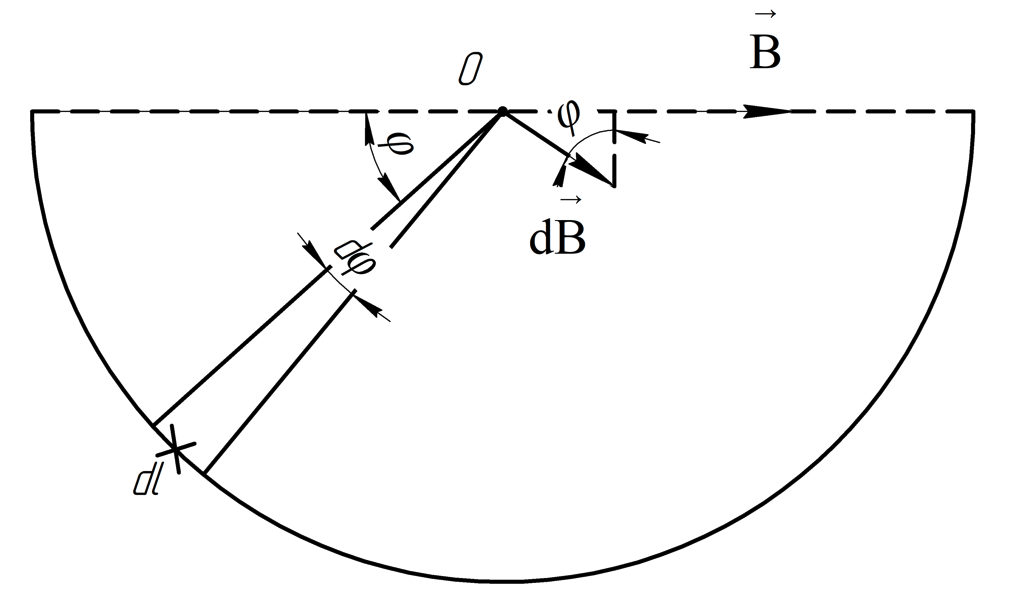Для
нахождения
в точне О необходимо просуммировать
проекции
от каждой элементарной нити на направление
Индукция всего проводника:
Индукцию одной элементарной нити вычислим по закону Био-Савара-Лапласа для магнитного поля бесконечно прямого тока:
Теперь вычислим индукцию всего проводника.
Ответ:
.
2.235.
Определить индукцию магнитного поля в
точке
,
если проводник с током
имеет вид, показанный на одном из
рисунков:
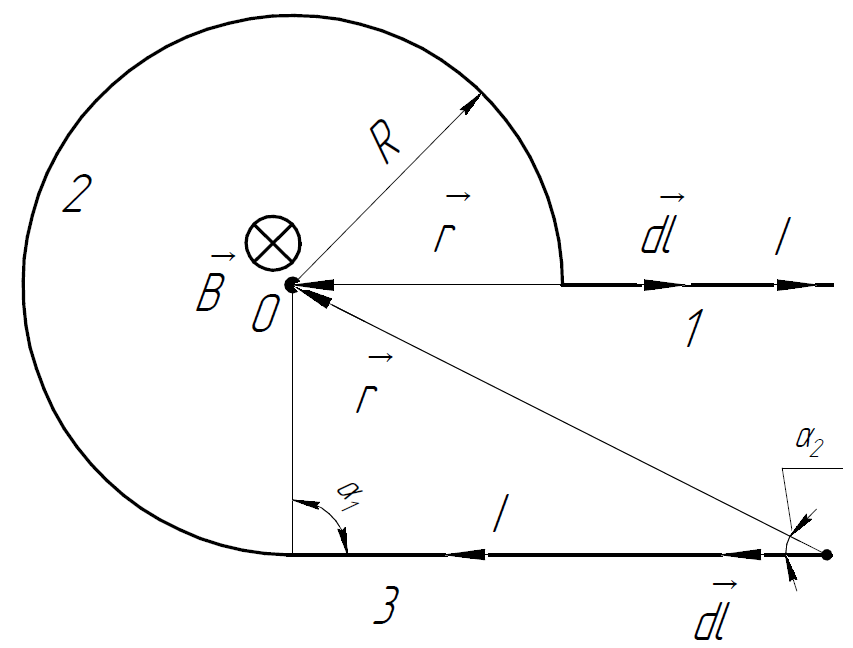Решение.
а) Разобьём контур на 3 участка, как
показано на рисунке:
По принципу суперпозиции для вектора магнитной индукции результирующее магнитное поле в точке можно представить следующим образом:
Модуль вектора магнитной индукции, можно найти с помощью закона Био-Савара-Лапласа:
Рассмотрим последовательно каждый участок.
На 1-м участке угол
между
и
,
проведённым к точке
,
всегда равен
,
следовательно результирующее магнитное
поле от данного участка
.
На 2-м участке
,
следовательно
направлен за плоскость рисунка, так как
вектора
составляют правую тройку. Магнитную
индукцию, как следует из закона
Био-Савара-Лапласа для участка кругового
проводника, можно вычислить следующим
образом:
На 3-м участке
,
следовательно результирующее магнитное
поле, создаваемое данным участком в
точке
.
Таким образом, результирующее магнитное поле в точке :
Ответ:
.
б) Аналогично прошлому пп. разобьём контур на 3 участка.
Магнитная индукция, создаваемая в точке :
Рассмотрим последовательно каждый участок:
На участке 1 угол между и равен , следовательно в точке .
На участке 2 направление можно определить по правилу правого винта: ток идёт по круговому проводнику по часовой стрелке, следовательно
направлен
за плоскость чертежа. Аналогично прошлому
пп. определяем
по закону Био-Савара-Лапласа для участка
кругового проводника:
Для участка 3 магнитное поле можно найти как поле отрезка прямого тока:
Направление
также можно определить по правилу
правого винта: в точке
направлен за плоскость чертежа.
Тогда результирующее магнитное поле в точке :
Ответ:
.
в) В данном случае проводник состоит из 2-х прямолинейных участков и полуокружности.
Вновь воспользуемся принципом суперпозиции для :
Согласно правилу правого винта, магнитное поле от каждого участка в точке будет направлено за плоскость чертежа, следовательно можем перейти к модулям:
Вычислим магнитное поле от участка 1 как поле прямолинейного проводника:
Аналогично для участка 3:
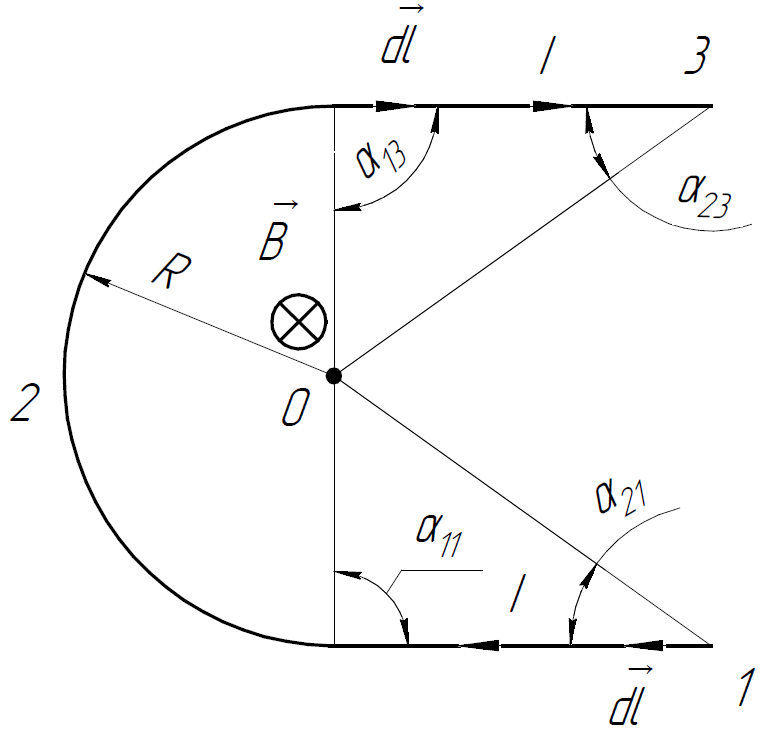Магнитную
индукцию, которую создаёт участок 2,
найдём как индукцию участка кругового
проводника:
Таким образом, результирующее магнитное поле в точке :
Ответ:
.
2.237 Длинный
проводник с током
изогнут под прямым углом. Найти магнитную
индукцию в точке, которая отстоит от
плоскости проводника на
и находится на перпендикуляре, проходящем
через точку изгиба.
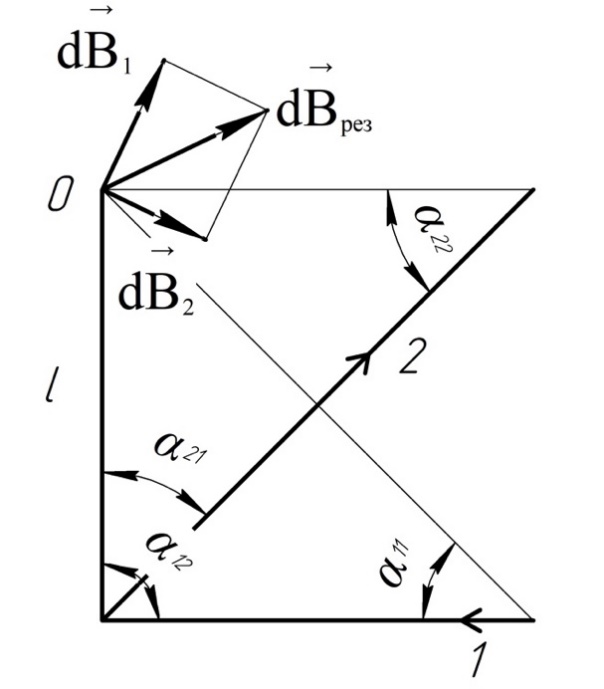Решение.
Разобьем проводник на два участка
и
.
Определим направление индукции в точке О по правилу правого винта.
Используем закон Био-Савара-Лапласа для поля прямого проводника:
– угол от начала проводника к точке
– угол от конца проводника в точке
: Определим направление индукции в точке О по правилу правого винта.
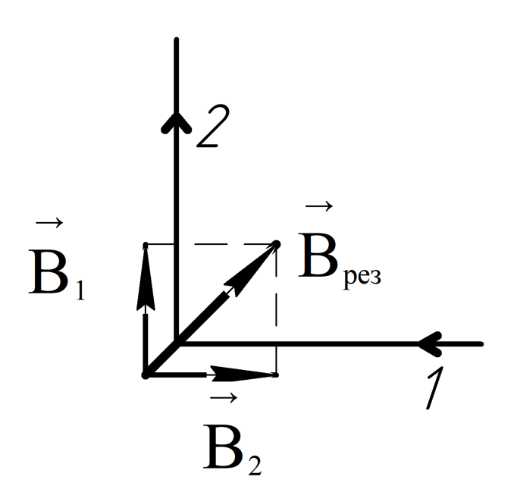Используем
закон Био-Савара-Лапласа для поля прямого
проводника:
Определим направление по принципу суперпозиции (результирующий вектор равен векторной сумме векторов).
Тогда для модуля :
Ответ:
.
2.239. Найти магнитную индукцию в точке , если проводник с током
имеет вид, показанный:
а) на рис. 1;
б) на рис. 2.
Радиус
изогнутой части проводника
,
прямоугольные участки проводника очень
длинные.
Решение. Разобьём проводник на участки, как показано на рисунке.
Согласно принципу суперпозиции для вектора магнитной индукции:
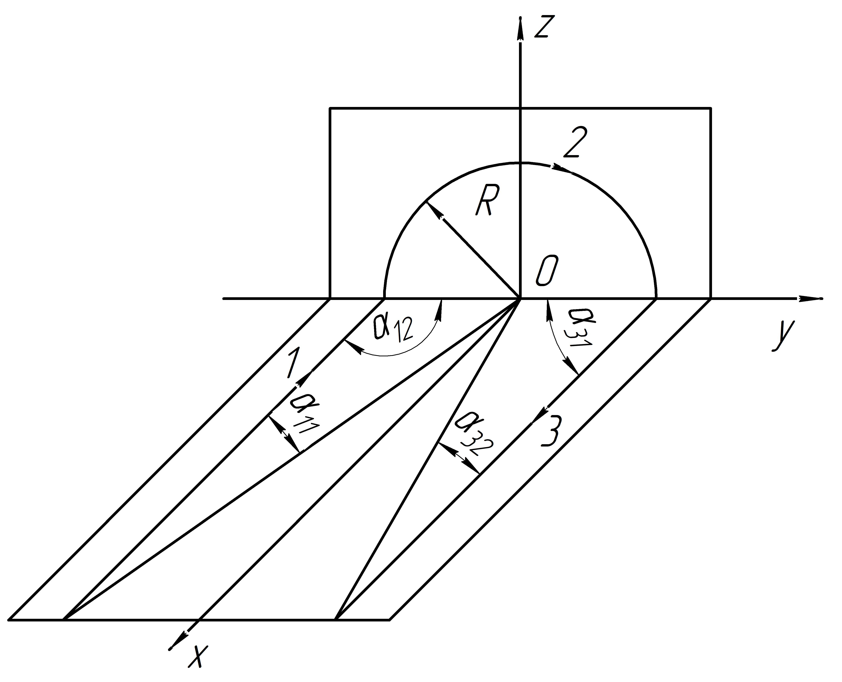Рис.1.
Участок 1:
Определим направление вектора
по правилу правого винта: он направлен
вертикально вниз. Используем закон
Био-Савара-Лапласа для поля отрезка
прямого тока (
).
Участок 2:
Определим направление вектора
по правилу правого винта: он направлен
от нас. Используем закон Био-Савара-Лапласа
для кругового проводника:
Участок 3:
Определим направление вектора
по правилу правого винта: он направлен
вертикально вниз. Используем закон
Био-Савара-Лапласа для поля отрезка
прямого тока (
.
– сонаправлены, следовательно:
б) Разобьем проводник на участки. Cогласно принципу суперпозиции:
Рис. 2.
Участок
1: Определим направление вектора
по правилу правого винта: он направлен
вертикально вниз. Используем закон
Био-Савара-Лапласа для поля отрезка
прямого тока (
).
Участок
2: Определим направление вектора
по правилу правого винта: он направлен
от нас. Используем закон Био-Савара-Лапласа
для кругового проводника:
Участок
3: Определим направление вектора
по правилу правого винта: он направлен
от нас. Используем закон Био-Савара-Лапласа
для поля отрезка прямого тока (
).
– сонаправлены, следовательно:
Ответ:
2.241. Определить индукцию магнитного поля тока, равномерно распределённого:
а) по плоскости
с линейной плотностью
.
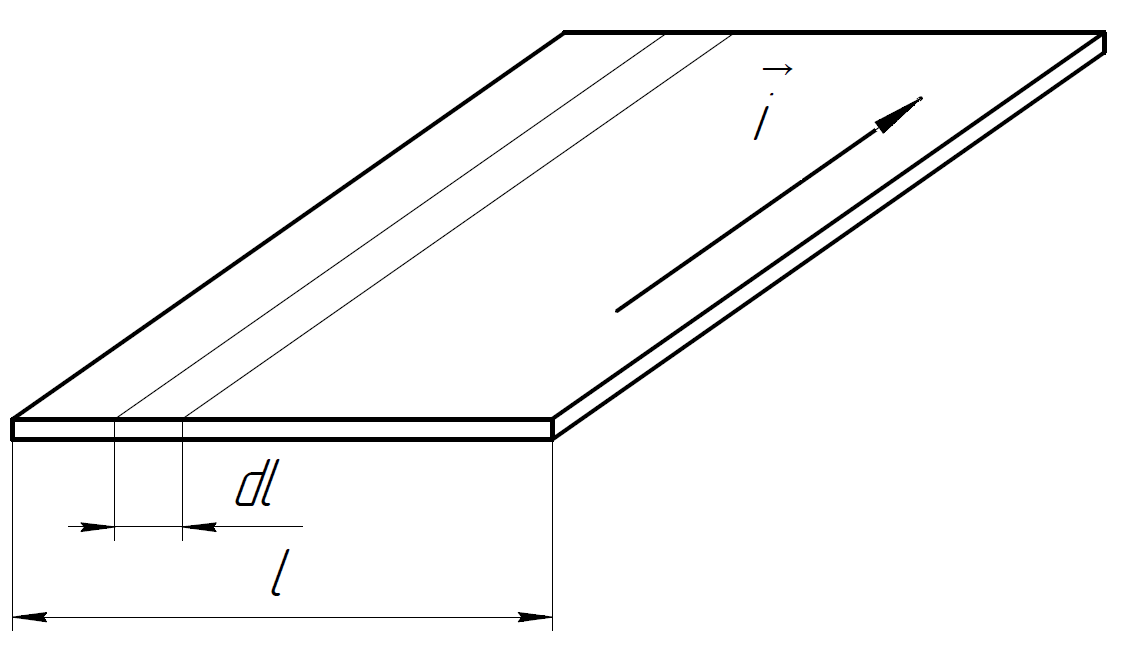Решение.
Мысленно поделим плоскость на узкие
полоски ширины
.
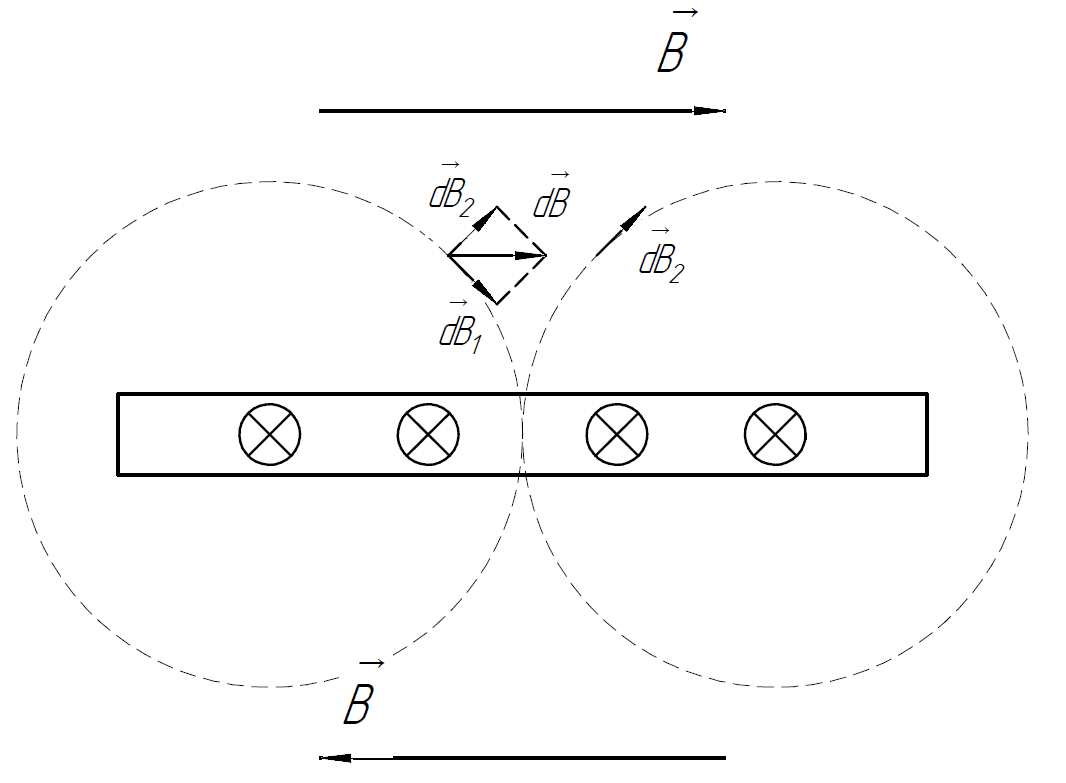Рассмотрим
часть плоскости в поперечном сечении.
Проведём силовые линии вектора магнитной индукции для 2-х участков ширины . Направления векторов , создаваемых этими участками, определим по правилу правого винта: в любой точке направлен по часовой стрелке по касательной к соответствующей силовой линии. Складывая магнитные поля от этих участков в каждой точке пространства, получаем, что над плоскостью направлен горизонтально вправо, под плоскостью – влево.
Для
нахождения модуля
применим теорему о циркуляции магнитного
поля:
В качестве замкнутого контура выберем прямоугольник с одной из сторон, равной и другой стороной произвольной длины. Будем обходить прямоугольник по часовой стрелке.
Вычислим
циркуляцию
.
На вертикальных сторонах прямоугольника
угол между
и
равен
и
,
следовательно интегрирование по
вертикальным сторонам не даёт вклад в
циркуляцию:
По определению линейной плотности тока:
Таким образом, из (2), (3) и (4) после сокращений получаем:
Ответ:
.
2.242
Однородный ток плотности
течет внутри неограниченной пластины
толщины 2d параллельно
ее поверхности. Пренебрегая влиянием
вещества пластины, найти индукцию
магнитного поля этого тока как функцию
расстояния x от средней
плоскости пластины.
Решение. Плотность тока по определению:
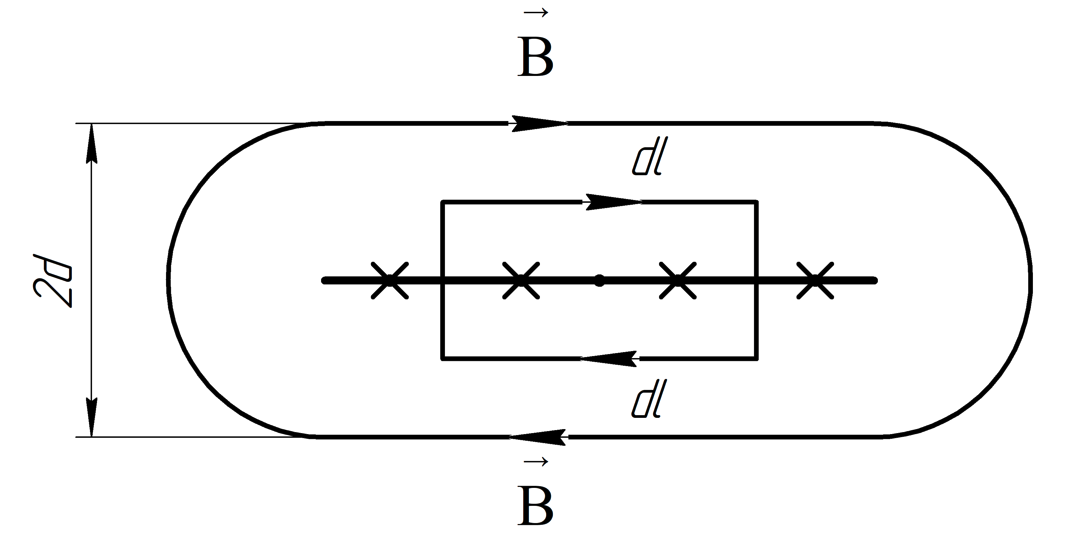Рассмотрим
пластину при
.
Используем контур, симметричный относительно центра пластины. В данном случае удобнее всего будет использовать прямоугольный контур.
Разобьем контур на участки:
Используем теорему циркуляции вектора
Вычисляем циркуляцию:
Получаем, что интегрируем только по горизонтальным сторонам треугольника:
Используем (5) в (3):
После вычисления интегралов получаем:
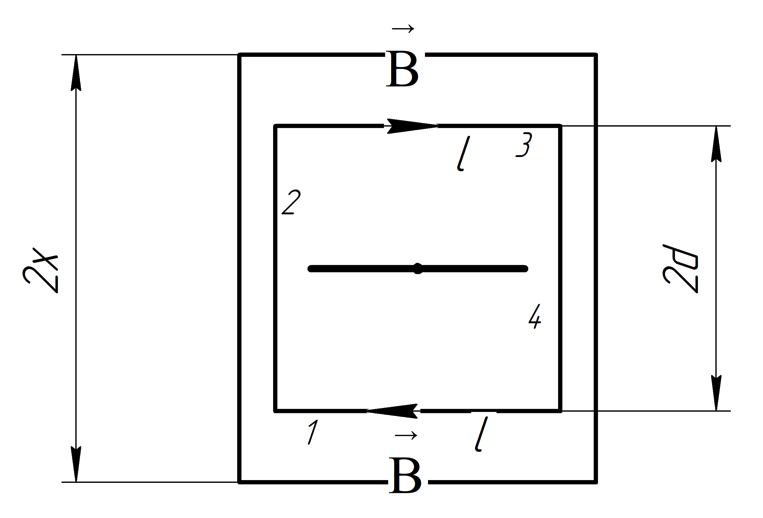Рассмотрим
пластину
.
Необходимо использовать контур, симметричный относительно плоскости. В нашем случае это прямоугольный контур.
Разобьем контур на участки. По принципу суперпозиции:
При ток будет течь лишь по толщине пластины 2d.
Используем теорему о циркуляции вектора
После вычисления интегралов получаем:
Ответ:
:
;
:
.
2.244. Ток
течет по длинному проводу и затем
растекается равномерно по всем
направлениям в однородной проводящей
среде. Пренебрегая влиянием вещества
среды, найти индукцию магнитного поля
в точке
,
отстоящей от точки
на расстояние
под углом
Решение.
Индукция в точке
определяется
по правилу правого винта. Используем
теорему о циркуляции вектора
В качестве контура интегрирования выбираем окружность:
Необходимо найти ток, охваченный контуром. Т.к. ток распределен равномерно, то плотность тока по углу равна:
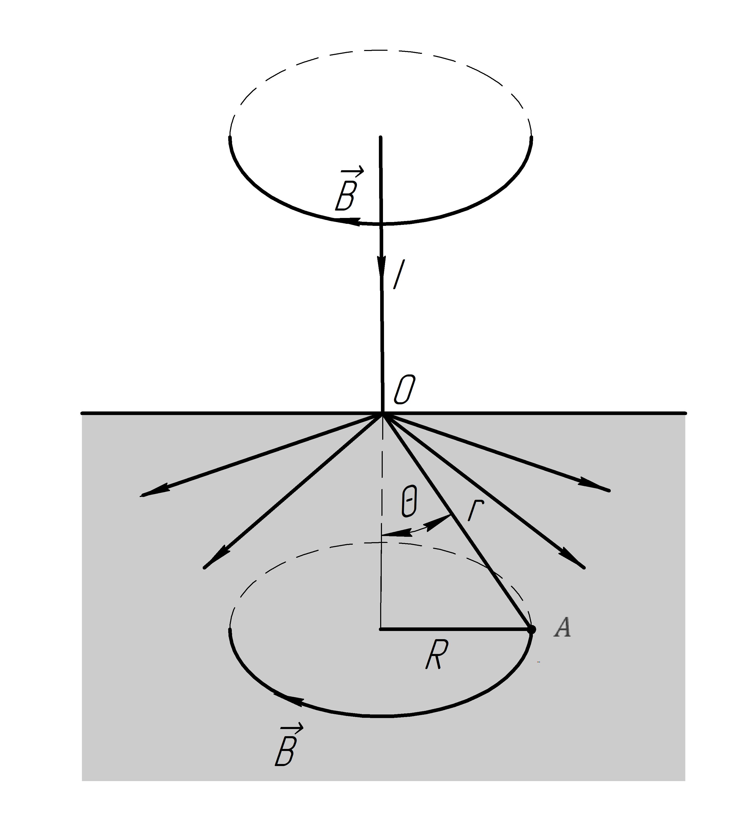
Тогда
весь ток:
Охваченный ток:
Находим
магнитную индукцию
с помощью (1):
Отсюда получаем:
Ответ:
2.246. По
прямому проводу, радиус сечения которого
,
течёт постоянный ток плотности
.
Пренебрегая влиянием вещества провода,
найти индукцию магнитного поля этого
тока в точке, положение которой
относительно оси провода определяется
радиус-вектором
.
Решение. Будем считать проводник бесконечно длинным.
Для определённости рассмотрим случай, когда ток направлен от нас за плоскость рисунка. Тогда направление можем определить по правилу правого винта: в любой точке окружности радиуса вектор магнитной индукции направлен по часовой стрелке.
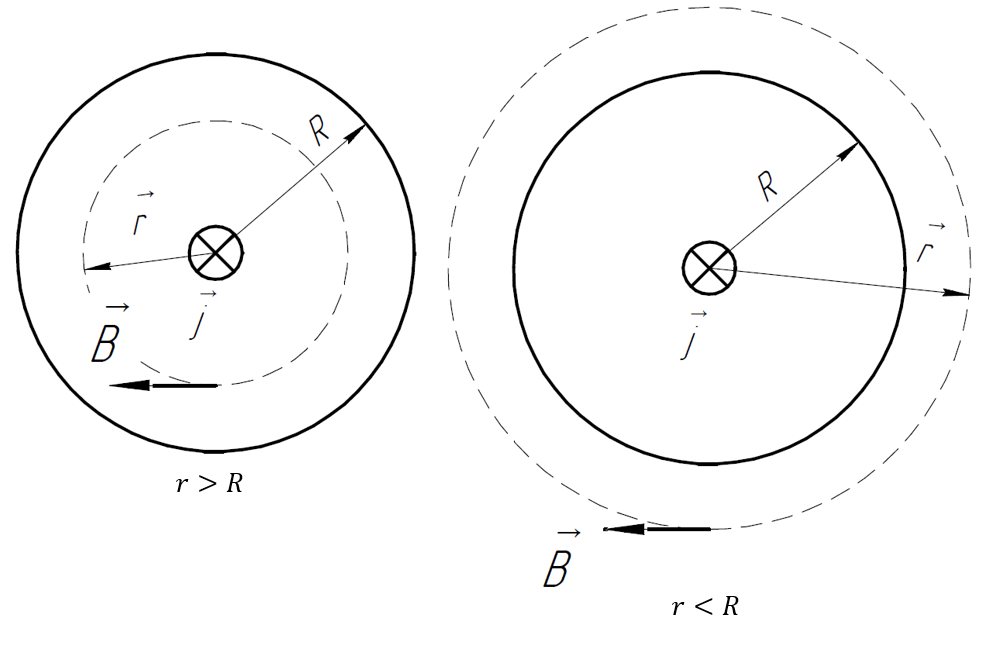Возможны
2 случая:
и
.
Модуль вектора магнитной индукции можем определить с помощью теоремы о циркуляции магнитного поля:
Выберем в качестве замкнутого контура окружность радиуса с центром в центре поперечного сечения проводника
Также выберем
направление обхода замкнутого контура
по часовой стрелке. Тогда угол между
векторами
и
= 0.
Получаем:
На окружности в виде выбранного нами замкнутого контура модуль постоянен. Также на всём поперечном сечении проводника постоянна плотность тока .
Получили:
Рассмотрим случаи и отдельно.
1) .
2) .
Введём
единичный вектор
.
Данный вектор совпадает по направлению
с вектором
в любой точке.
Тогда вектор магнитной индукции в любой точке можно представить в виде:
Ответ:
.
2.247. Внутри длинного прямого провода круглого сечения имеется длинная круглая цилиндрическая плоскость, ось которой параллельна оси провода и смещена относительно последней на расстояние 1. По проводу течет постоянный ток плотность j. Пренебрегая влиянием вещества провода, найти индукцию магнитного поля внутри полости.
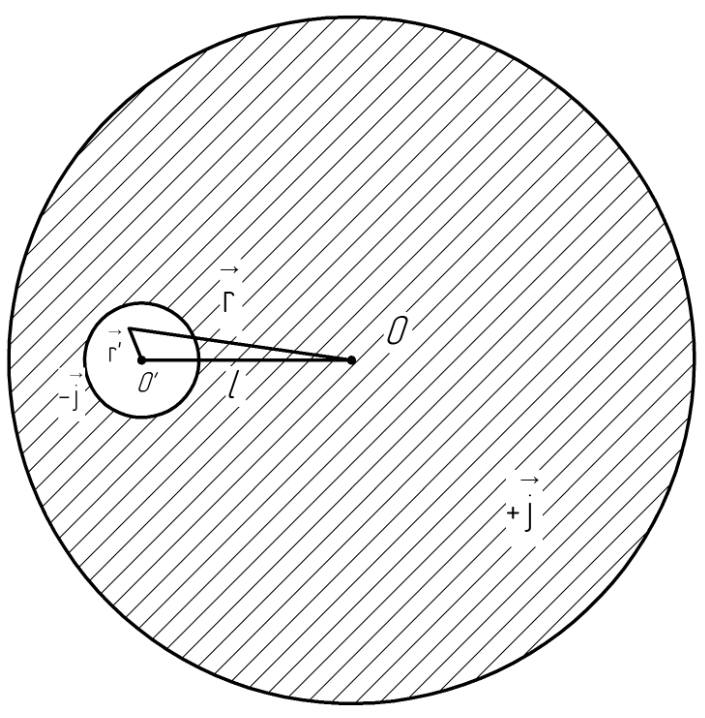Решение.
Вид с торца:
Из рисунка:
Согласно принципу суперпозиции вектора магнитной индукции
- магнитная индукция целостного проводника
- магнитная индукция в точке полости
Вычислим магнитную индукцию целостного проводника.
Допустим, ток направлен от нас. Согласно правилу правого винта определим направление индукции.
Используем теорему о циркуляции 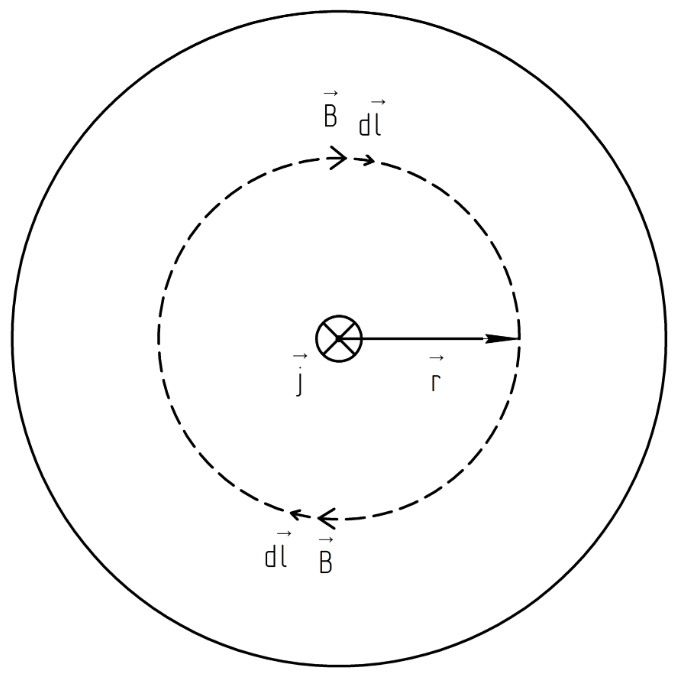вектора .
В
качестве контура интегрирования выберем
окружность радиуса
.
Направление обхода контура выберем
совпадающим с направлением вектора
.
Вычислив интегралы, получаем:
Таким образом, магнитная индуция целостного проводника:
где
– единичный вектор.
Тогда в векторном виде индукция целостного проводника:
Теперь найдём магнитную индукцию полости.
Направим ток от нас. Магнитную индукцию определим по правилу правого винта.
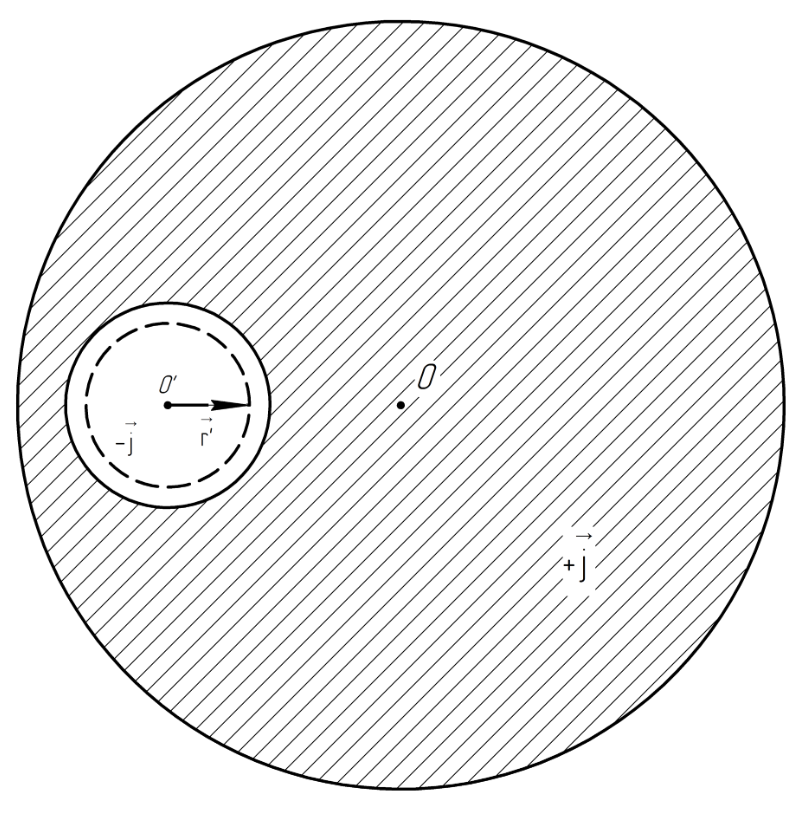Используем
теорему о циркуляции вектора
.
Отсутствие тока в полости эквивалентно тому, что полость заполнена тем же током, что и провод, но с противоположным знаком.
где – единичный вектор.
Тогда в векторном виде получаем:
Можем найти искомую магнитную индукцию:
Ответ:
.
2.248. Найти
плотность тока как функцию расстояния
от оси аксиально-симметрично параллельного
потока электронов, если индукция
магнитного поля внутри потока
,
где
и
– положительные постоянные.
Решение. Допустим, ток течет вниз. По правилу правого винта определяем направление магнитной индукции.
Выберем контур – окружность с центром, совпадающим с центром потока и радиусом . Направление обхода контура выберем совпадающим с направлением магнитной индукции.
Используем
теорему о циркуляции вектора
.
Из рисунка можно увидеть, что:
Вычислим циркуляцию:
Подставив (3) в (1), получаем для плотности тока:
Ответ:
2.252. На
деревянный тороид малого поперечного
сечения намотано равномерно
витков провода, по которому течёт ток
.
Найти отношение
магнитной индукции внутри тороида к
индукции в его центре.
Решение. Предположим, что ток течёт по тороиду по часовой стрелке.
Для начала найдём магнитное поле внутри тороида.
Воспользуемся
теоремой о циркуляции. Так как всего на
тороид намотано
витков, то суммарный ток, протекающий
через его поперечное сечение, составит
.
Силовые линии в данном случае – окружности с центром на оси тороида.
Выберем в качестве замкнутого контура окружность радиуса , которая проходит через середину сечения тороида и центр которой лежит на оси тороида. На этой окружности модуль постоянен.
Сначала вычислим циркуляцию.
Получаем
следующее магнитное поле внутри тороида:
Магнитное поле в центре тороида найдём с помощью закона Био-Савара-Лапласа как поле кругового проводника с током.
Найдём отношение магнитной индукции внутри тороида к индукции в его центре:
Ответ:
.
2.254.
Имеется длинной соленоид с током
Площадь его поперечного сечения
,
число витков на единицу длины
.
Найти магнитный поток через торец
соленоида.
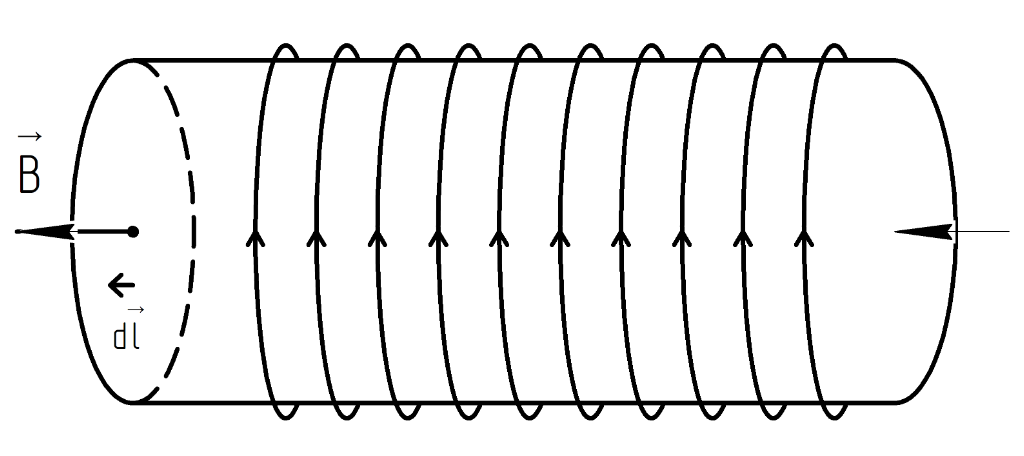Решение.
Воспользуемся теоремой о циркуляции
вектора B (для соленоида).
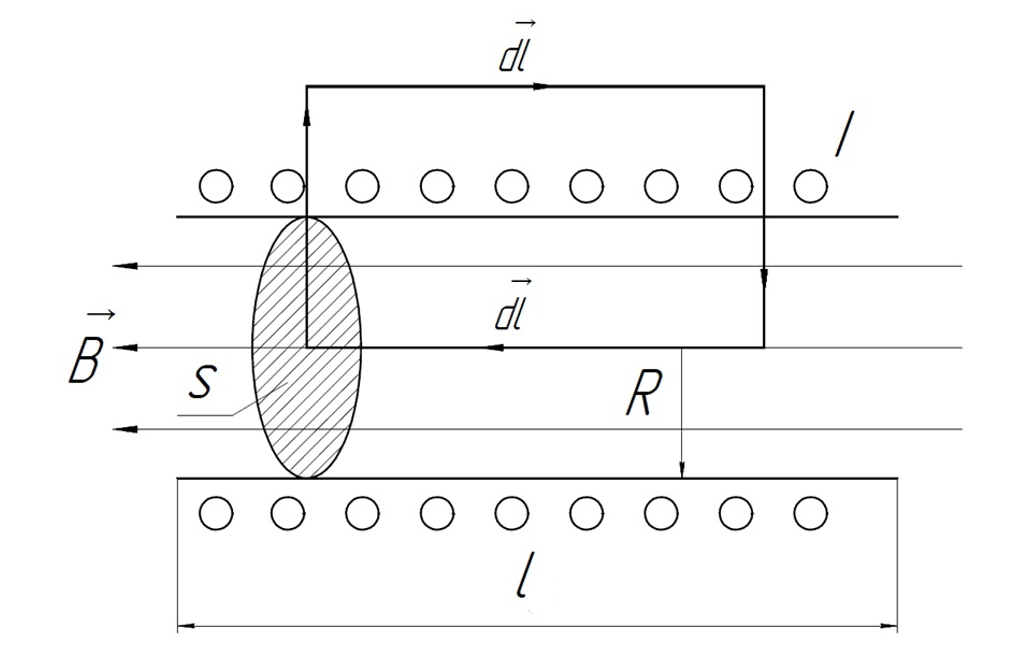В
качестве контура интегрирования будем
использовать прямоугольник. Разобьём
криволинейный интеграл на интеграл по
соответствующим участкам:
Вычислим циркуляцию (магнитное поле за пределами соленоида отсутствует):
Окончательно получаем:
Вернёмся к теореме о циркуляции и выразим магнитную индукцию:
Найдем магнитный поток.
В середине соленоида:
Если брать теорему о циркуляции вектора по соленоиду (бесконечному), то сначала стоит рассмотреть весь соленоид:
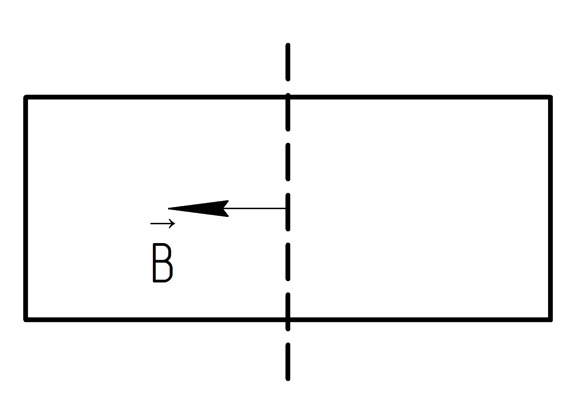
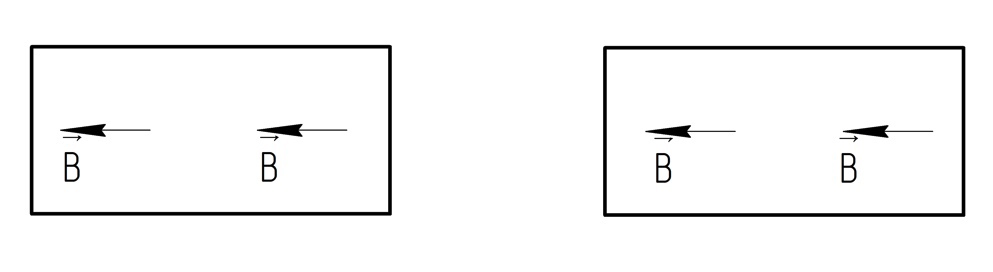А
после разделим рассматриваемый соленоид
пополам:
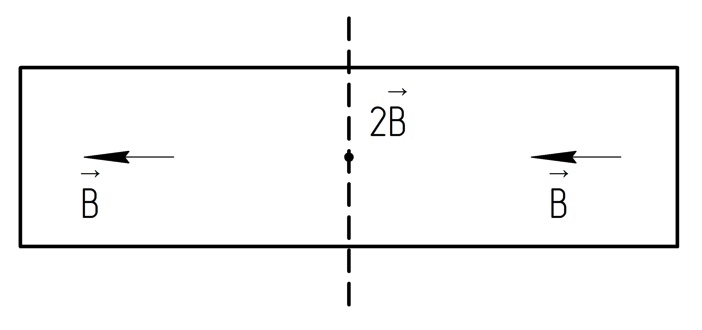И
соединим вместе:
И тогда магнитная индукция на торце соленоида в 2 раза меньше, чем внутри.
Снаружи
соленоида
(пренебрежимо малое), следовательно
магнитный поток:
Ответ:
.
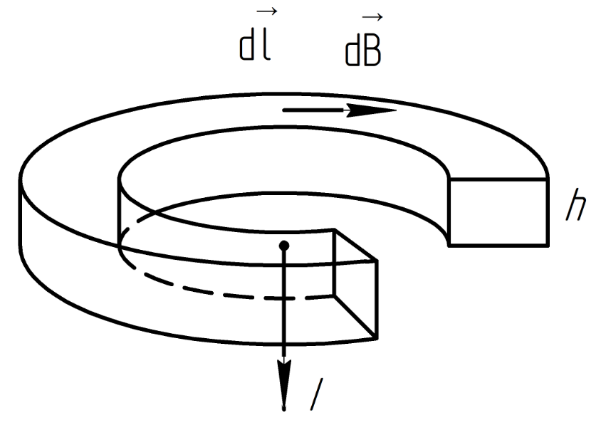2.255
На рисунке показан кольцевой соленоид
прямоугольного сечения. Найти магнитный
поток через это сечения, если ток в
обмотке
,
полное число витков
,
отношение внешнего диаметра к внутреннему
и толщина
.
Решение. Допустим, ток направлен от нас, определим направление магнитной индукции по правилу правого винта, выберем соответствующее направление обхода.
Используем теорему о циркуляции вектора для соленоида.
Получаем модуль магнитной индукции:
Определим
магнитный поток через поперечное
сечение. По определению магнитного
потока:
Из рисунка можно увидеть, что:
Ответ:
.
2.265. Найти
модуль и направление силы, действующей
на единицу длины тонкого проводника с
током
в точке О.
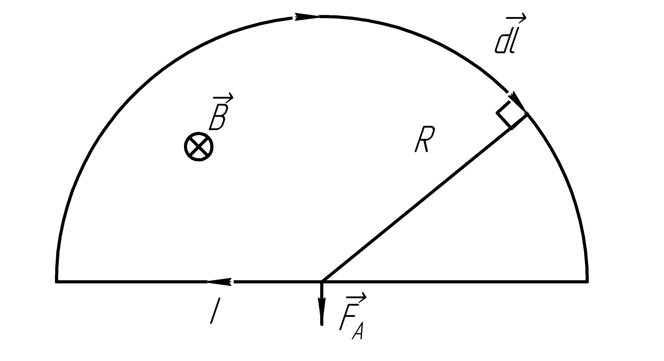Решение.
а)
.
Определим магнитную индукцию с помощью закона Био-Савара-Лапласа для кольцевого прводника:
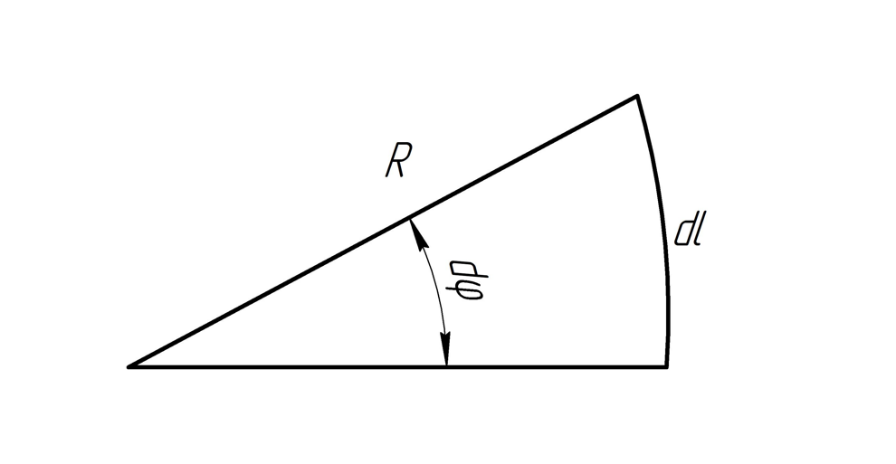Из
рисунка видно, что:
Тогда получаем:
По определению
силы Ампера (
т.к.
):
Сила
Ампера в точке О ((
т.к.
):
Б)
,
.
Определим направление магнитной индукции по правилу правого винта, с помощью правила левой руки определим направления сил Ампера.
компенсирует
и вместе они обращаются в ноль.
Найдем индукцию на участке 2. Используем формулу Био-Савара-Лапласа для проводника отрезка прямого тока:
Сила Ампера
для прямолинейного проводника (
т.к.
(угол между
и
)):
Ответ:
.
2.271. Замкнутый
контур с током
находится
в поле длинного прямого проводника с
током
.
Плоскость контура перпендикулярна
прямому проводнику. Найти момент сил
Ампера, действующих на замкнутый контур,
если он имеет вид:
а) как на рис. 1;
б) как на рис. 2.
Решение.
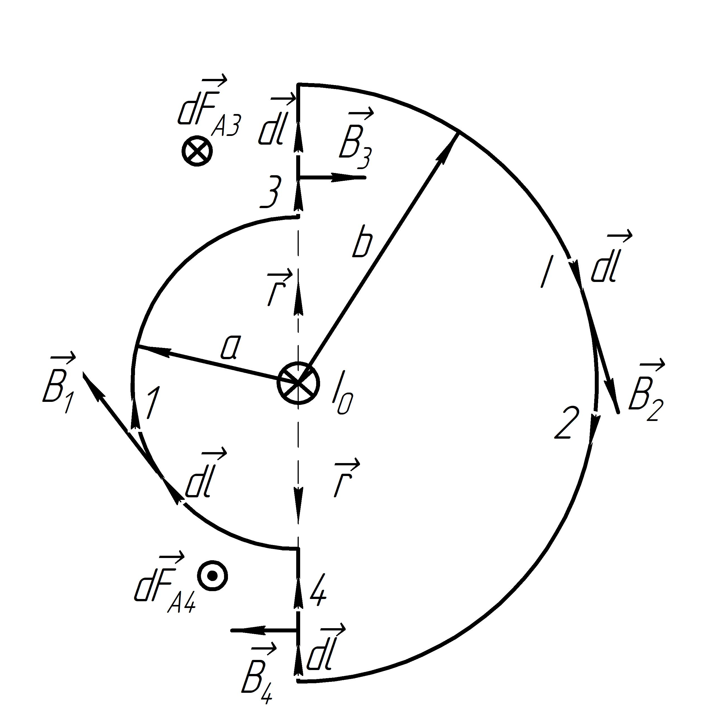a)Разделим
контур на участки (Рис. 1):
Рассмотрим участки по отдельности.
Определим направление магнитной индукции по правилу правого винта.
следовательно:
.
следовательно:
следовательно:
следовательно:
Таким образом, силы Ампера будут действовать лишь на прямые отрезки контура.
На замкнутый контур будет действовать вращающий момент. На (3) сила направлена вниз (от нас), на (4) – вверх (к нам).
Магнитное поле прямого проводника будет пытаться повернуть контур с током.
Магнитная индукция, действующая на бесконечно длинный проводник с током , согласно закону Био-Савара-Лапласа:
Момента силы Ампера:
Перейдём к модулям:
Рассмотрим прямолинейные участки:
3:
сонаправлено с
,
следовательно
.
После вычисления интеграла получаем:
4:
и
направлены в противоположные стороны,
следовательно
.
Полный момент:
.
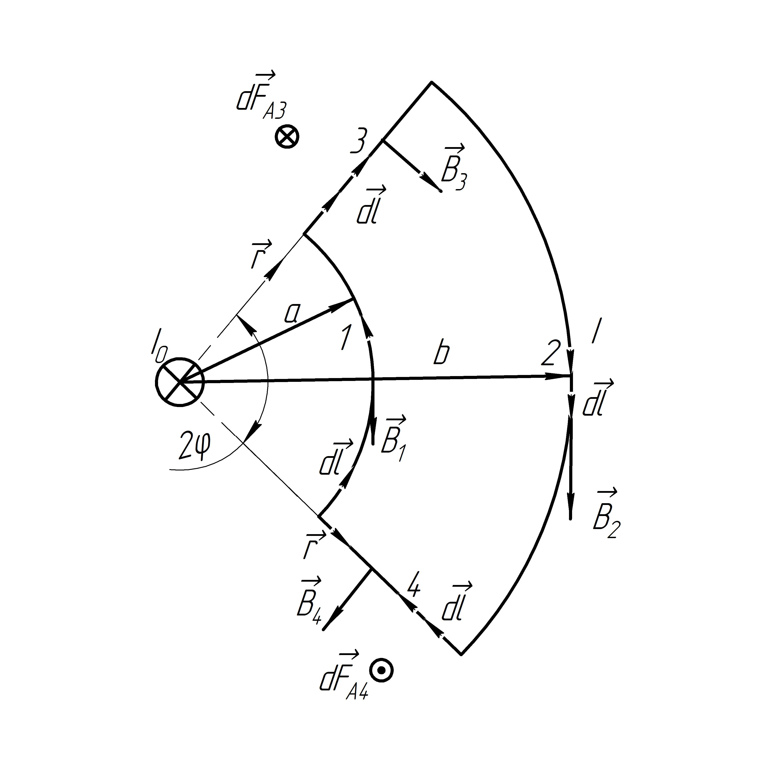б)
Разделим контур на участки. Определим
направление магнитной индукции по
правилу правого винта (левой руки):
следовательно: .
следовательно:
следовательно:
следовательно:
Силы Ампера будут действовать лишь на прямые отрезки контура.
На замкнутый контур будет действовать вращающий момент. На (3) сила направлена вниз (от нас), на (4) – вверх (к нам).
Магнитное поле прямого проводника будет пытаться повернуть контур с током.
Магнитная индукция, создаваемая на бесконечно длинным проводником с током , согласно закону Био-Савара-Лапласа:
Момент силы Ампера:
Рассмотрим участки:
3: сонаправлено с , следовательно .
После вычисления интеграл получаем:
4: и направлены в противоположные стороны, следовательно .
Суммарный вращающий момент:
Ответ:
2.273. Квадратная
рамка с током
расположена в одной плоскости с длинным
прямым проводником, по которому течёт
ток
.
Сторона рамки
.
Проходящая через середины противоположных
сторон ось рамки параллельна проводу
и отстоит от него на расстояние, которое
в
раза больше стороны рамки. Найти:
а) амперову силу, действующую на рамку;
б) механическую работу, которую нужно совершить при медленном повороте рамки вокруг её оси на .
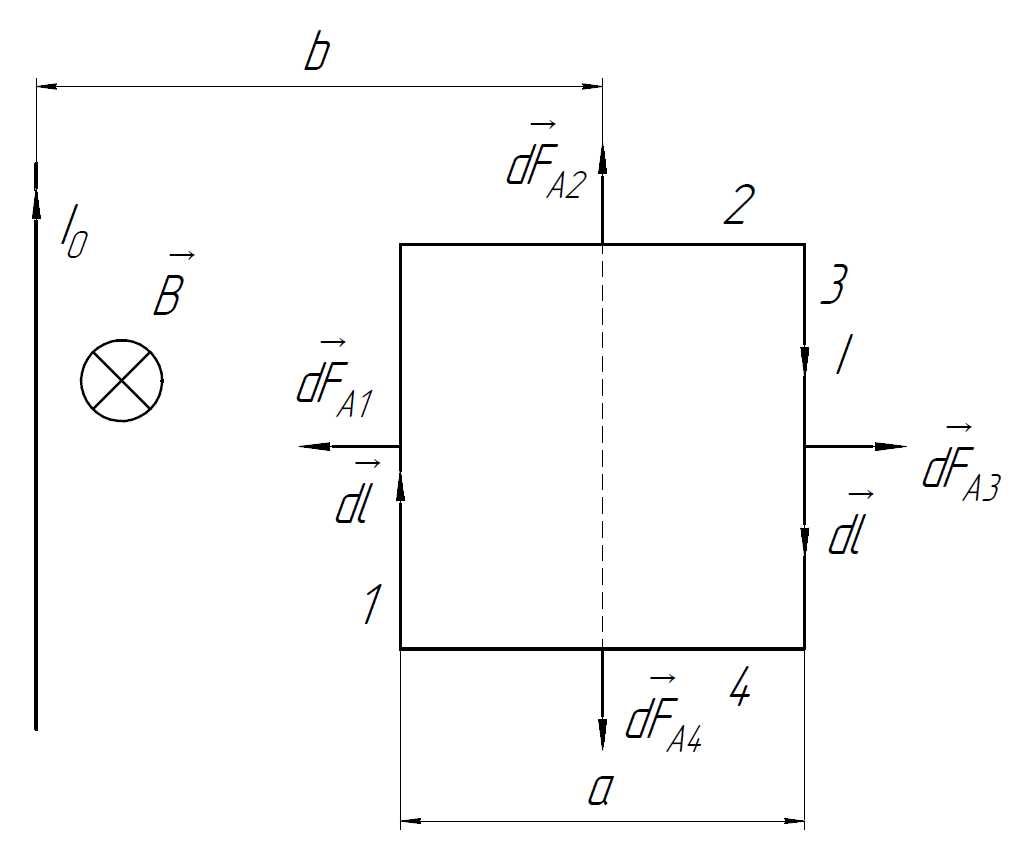Решение.
а) Направим ток в прямолинейном
проводнике вверх. Тогда по правилу
правого винта магнитное поле, создаваемое
данным проводником, направлено
перпендикулярно плоскости рамки «от
нас».
Модуль вектора магнитной индукции на расстоянии от прямолинейного проводника можем найти как поле бесконечно длинного проводника с током по закону Био-Савара-Лапласа:
Разобьём контур на 4 участка и определим направление силы Ампера, действующей на рамку с током на каждом участке, по правилу левой руки.
Сила Ампера – это сила, действующая на проводник с током, находящийся в магнитном поле:
Для соответствующих точек сторон 2 и 4 рамки расстояние до прямолинейного проводника одинаково, однако ток течёт в разные стороны, следовательно сила Ампера, действующая на данные участки, взаимно компенсируется.
Так как по рамке течёт постоянный ток , магнитная индукция постоянна на сторонах 1 и 3, то для сил, действующих на эти стороны, можем записать:
Результирующую
силу, действующую на рамку, найдём как
разность модулей
и
,
так как данные силы направлены в
противоположные стороны.
Ответ:
.
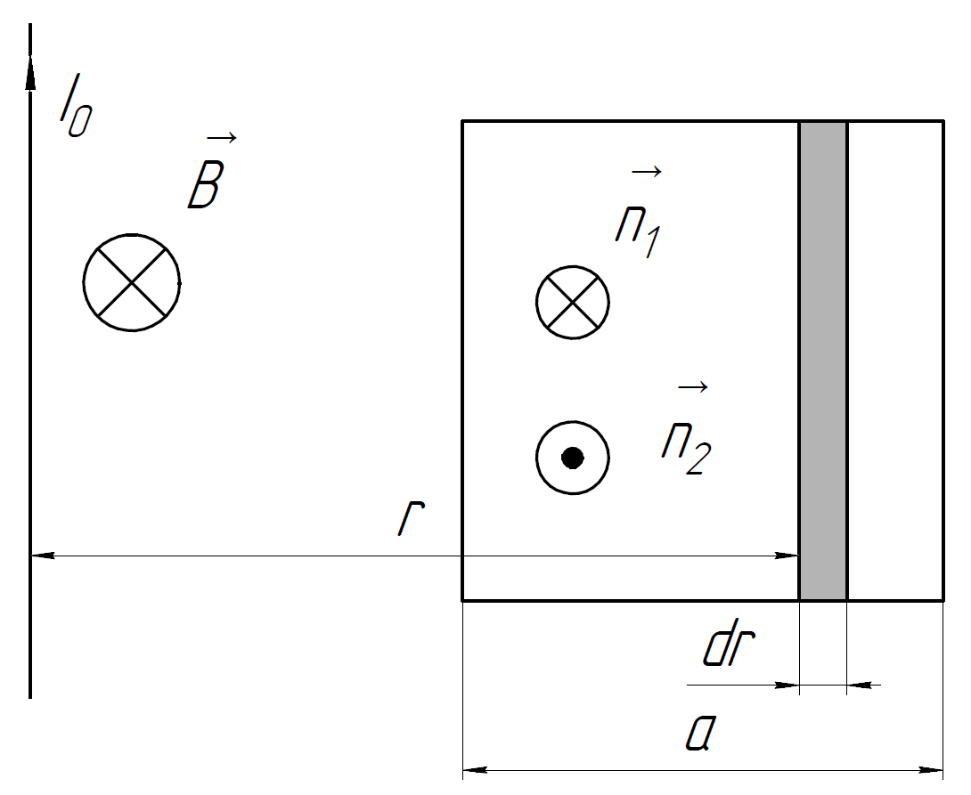б)
Механическая работа, которую необходимо
совершить, чтобы повернуть рамку на
вокруг своей оси, равна взятой с обратным
знаком работе, которую совершает
магнитное поле:
Магнитный поток по определению:
При повороте
рамки на
все её положения кроме крайних вклада
в изменение потока не дают, так как
вектор
поворачивается и принимает взаимно
обратные направления.
Тогда изменение потока при повороте рамки вокруг своей оси:
В начальном
положении
и
сонаправлены:
В конечном
положении
и
направлены в противоположные стороны.
Тогда
.
Таким образом, для поворота рамки на требуется совершить работу:
Ответ:
.
2.274 Два параллельных длинных провода с током I = 6,0 А в каждом (токи направлены в одну сторону) удалили друг от друга так, что расстояние между ними стало в = 2,0 раза больше первоначального. Какую работу на единицу длины проводов совершали при этом силы Ампера?
Решение.
Провода параллельны и токи в них сонаправлены, следовательно они притягиваются. Поэтому работа по удалению будет отрицательной.
Магнитная индукция длинного прямолинейного проводника с током согласно закону Био-Савара-Лапласа:
Воспользуемся определением силы Ампера:
Работа
силы Ампера:
В расчёте на единицу длины получаем:
Ответ:
.
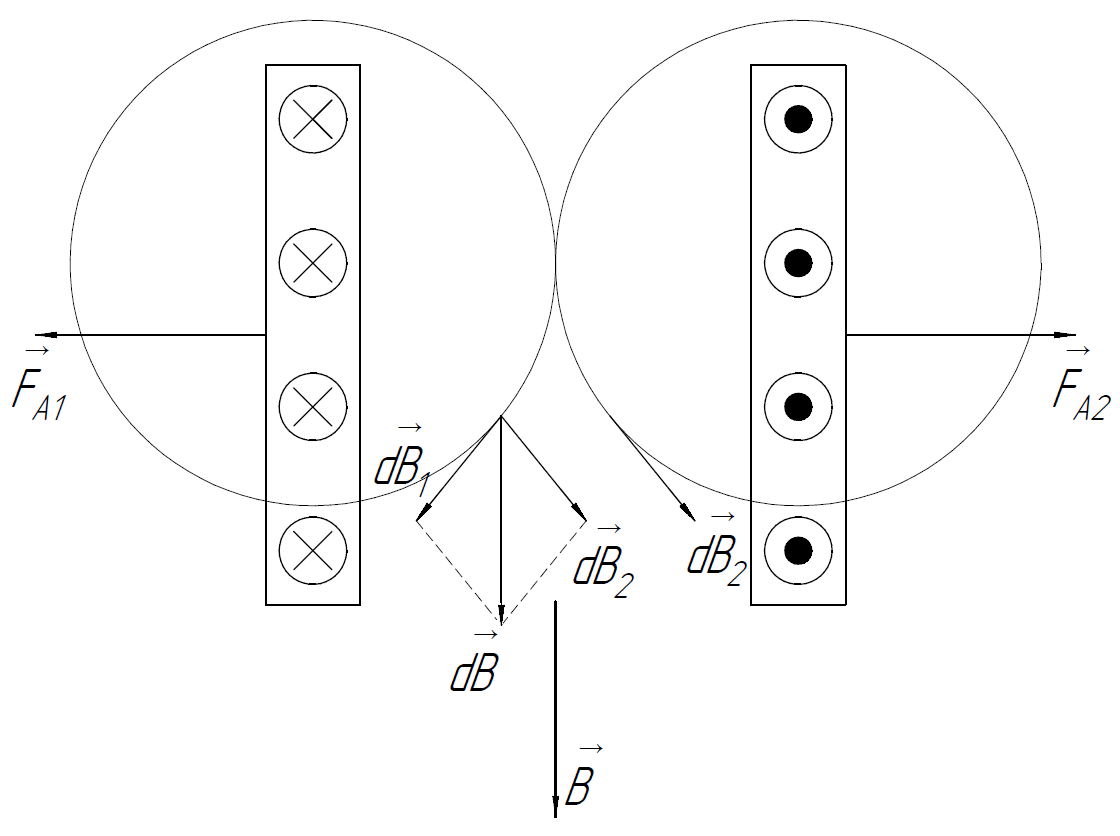2.279.
Система состоит из двух параллельных
друг другу плоскостей с токами, которые
создают между плоскостями однородное
магнитное поле с индукцией
.
Вне этой области магнитное поле
отсутствует. Найти магнитную силу,
действующую на единицу поверхности
каждой плоскости.
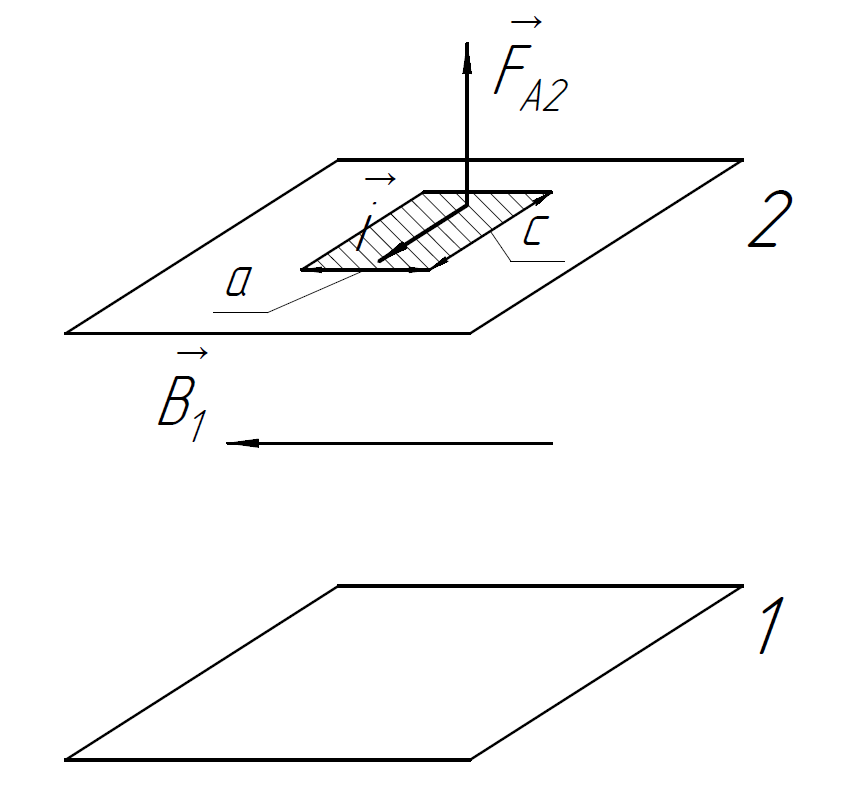
Решение. Так как вне пространства между плоскостями магнитное поле отсутствует, то токи, текущие по плоскостям, разнонаправлены, причём их численные значения одинаковы. Следовательно, в пространстве между плоскостями вектора их магнитной индукции сонаправлены (а модули векторов магнитной индукции равны), и рассматриваемые плоскости отталкиваются.
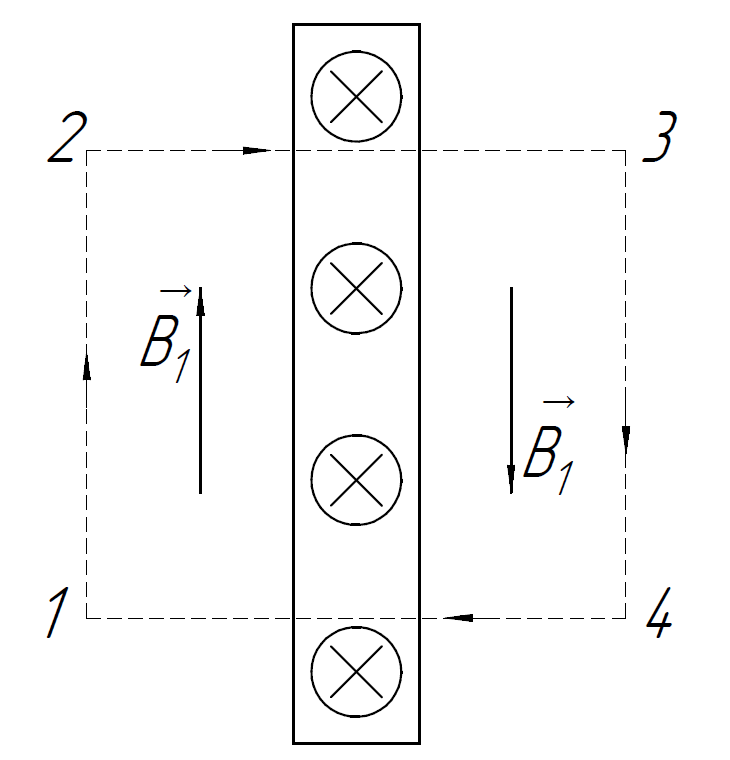Рассмотрим
одну из плоскостей отдельно от другой.
Воспользуемся теоремой о циркуляции
для вектора
для нахождения её магнитного поля:
В качестве замкнутого контура для вычисления циркуляции возьмём прямоугольник, сторона 1-2 которого равна , представленный на рисунке.
Так как угол между векторами и меняется при движении по контуру, необходимо разбить интеграл на 4 части:
После упрощения получаем:
Тогда согласно теореме о циркуляции (1):
Так как токи равны, то в пространстве между плоскостями:
Теперь найдём
силу тока, протекающего по одной из
плоскостей. Выделим на ней произвольную
прямоугольную площадку со сторонами
и
.
Пусть по
плоскости течёт ток с линейной плотностью
Тогда соответствующая ему сила тока:
Из (5) получим выражение для линейной плотности тока:
Теперь найдём силу, действующую на плоскость 2 со стороны плоскости 1.
Если проводник с током поместить в магнитное поле, то на него будет действовать сила Ампера:
Так
как в рассматриваемом случае сила тока
и магнитное поле постоянны, то для силы
Ампера, действующей на плоскость 2, можем
записать:
Такая же по модулю, но противоположная по направлению сила действует на плоскость 1. Перепишем (9) с учётом (5) и (6):
Получаем силу, действующую на единицу поверхности каждой плоскости:
Ответ:
.
2.289 Небольшой
виток с током находится на расстоянии
от длинного прямого проводника с током
.
Магнитный момент витка равен
.
Найти модуль и направление силы,
действующей на виток, если вектор
а) параллелен прямому проводнику;
б)
направлен по радиусу-вектору
Решение:
а) Сила, действующая на виток с током в неоднородном магнитном поле:
В
нашем случае
,
следовательно в направлении нормали к
витку индукция не изменяется:
,
т. е.
.
б) В данном
случае
.
Запишем вектор магнитной индукции:
Из (2) можно увидеть, что:
По закону Био-Савара-Лапласа для поля бесконечного прямого тока:
Так как магнитное поле неоднородно:
Ответ:
.
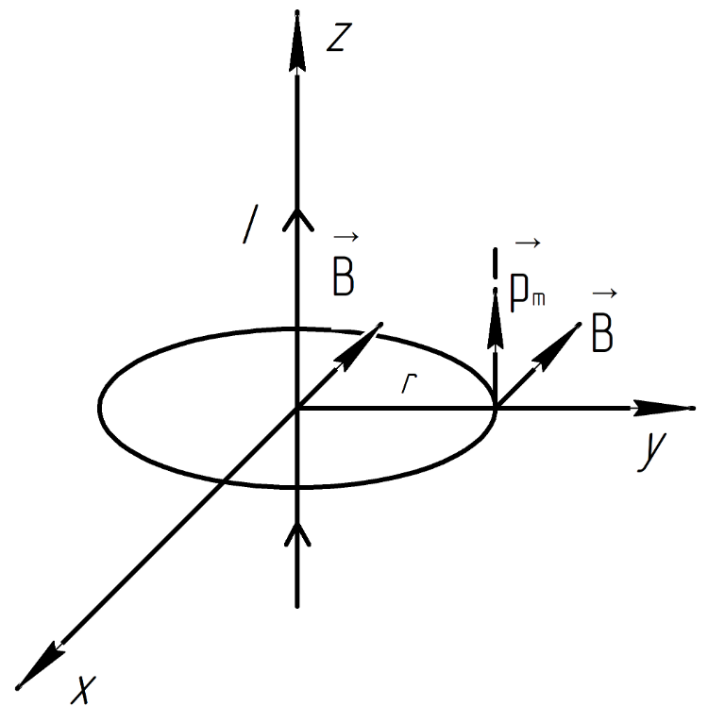
2.290. Небольшая катушка с током, имеющая магнитный момент , находится на оси кругового витка радиуса , по которому течет ток . Найти модуль силы, действующей на катушку, если ее расстояние от центра витка равно , а вектор совпадает по направлению с осью витка.
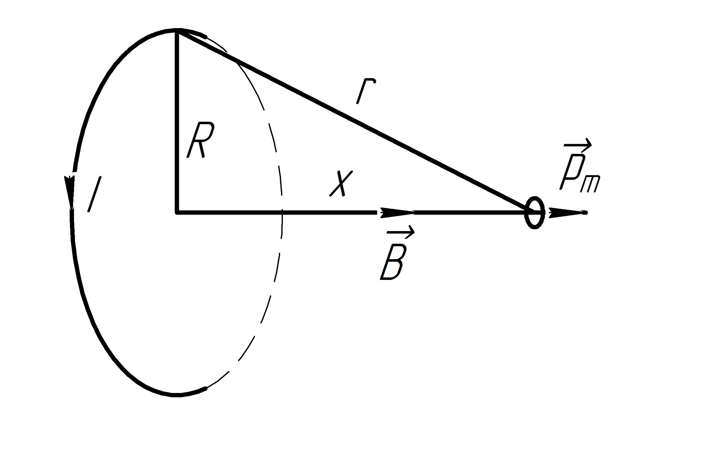Решение.
Магнитная индукция на оси кругового тока по закону Био-Савара-Лапласа:
Так как магнитное поле неоднородное, то на катушку действует сила:
В нашем случае
.
2.291. Найти
силу взаимодействия двух катушек с
магнитным моментом
и
,
если их оси лежат на одной прямой и
расстояние между катушками
, значительно превышает их линейные
размеры.
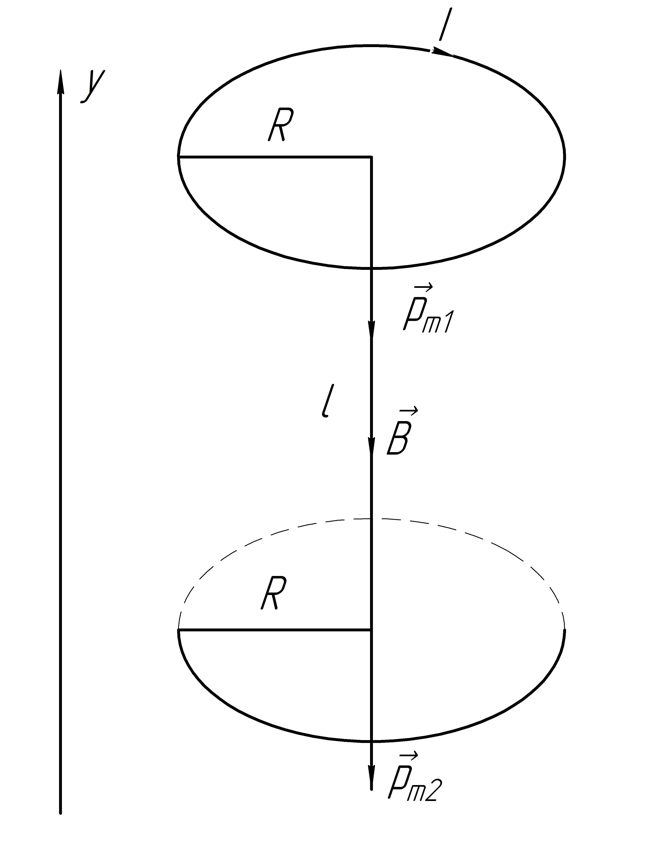Решение.
По правилу правого винта определим
направление
.
Cилу, действующую на одну из катушек, создает магнитное поле другой катушки. Так как магнитное поле кругового витка с током неоднородное, то:
В нашем случае
,
следовательно:
Магнитная индукция на оси кругового тока по Био-Савара-Лапласа (для 2 кольца):
, следовательно:
Ответ:
.
2.293. Индукция
магнитного поля в вакууме вблизи плоской
поверхности однородного изотропного
магнетика равна
,
причём вектор
составляет угол
с нормалью к поверхности. Магнитная
проницаемость магнетика
.
Найти индукцию
магнитного поля в магнетике вблизи
поверхности.
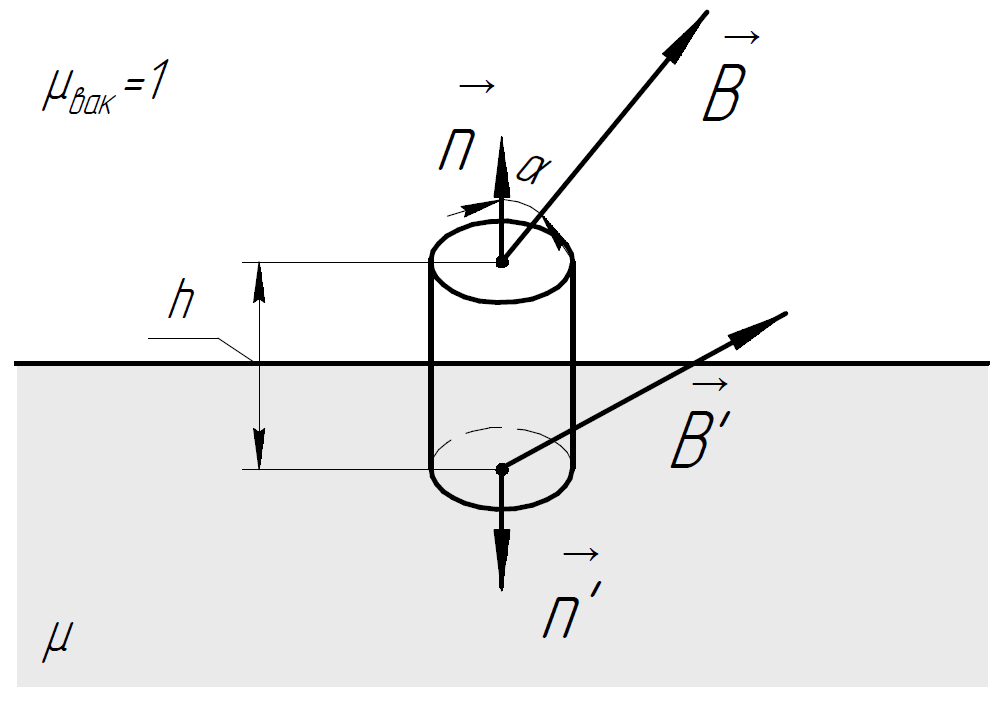Решение.
Воспользуемся теоремой Гаусса для
вектора магнитной индукции:
В качестве гауссовой поверхности возьмём цилиндр, расположенный на границе раздела двух сред, высота которого пренебрежимо мала. Потоком через боковую поверхность так ого цилиндра можно пренебречь.
Воспользуемся теоремой Гаусса:
Для нормальной
составляющей
получаем:
Далее
воспользуемся теоремой о циркуляции
вектора
:
Так как токи
проводимости отсутствуют, то циркуляция
для любого замкнутого контура будет
равна
.
В
качестве контура для вычисления
циркуляции выберем прямоугольник с
пренебрежимо малой высотой. Тогда
вкладом в циркуляцию от его вертикальных
сторон можно пренебречь.
Будем обходить контур по часовой стрелке.
Вычислим циркуляцию:
Таким образом,
для
получаем:
Связь для векторов и :
Используя данную связь для (6), получаем:
Тангенциальная
и нормальная составляющие
взаимно перпендикулярны, следовательно
магнитное поле в магнетике:
Ответ:
.
2.296.
Длинный соленоид заполнен неоднородным
парамагнетиком, восприимчивость которого
зависит только от расстояния
до оси соленоида как
,
где, а - постоянная. На оси соленоида
индукция магнитного поля равна
.
Найти зависимость от
:
a) намагниченности
магнетика
;
б) плотности
молекулярного тока
в магнетике.
Решение.
а) По условию задании о токе проводимости
в магнетике ничего не сказано, поэтому
принимаем
.
Используем теорему о циркуляции вектора :
В качестве контура интегрирования возьмем прямоугольник, лежащий на оси соленоида, с пренебрежимо малой высотой.
Вектор намагниченности:
Или для
модуля, так как вектора
и
сонаправлены:
Относительная магнитная проницаемость:
Связь напряжённости магнитного поля с индукцией:
Тогда для
намагниченности получаем (с учётом
):
Ответ:
.
б) Плотность молекулярного тока по определению:
Используем теорему о циркуляции вектора :
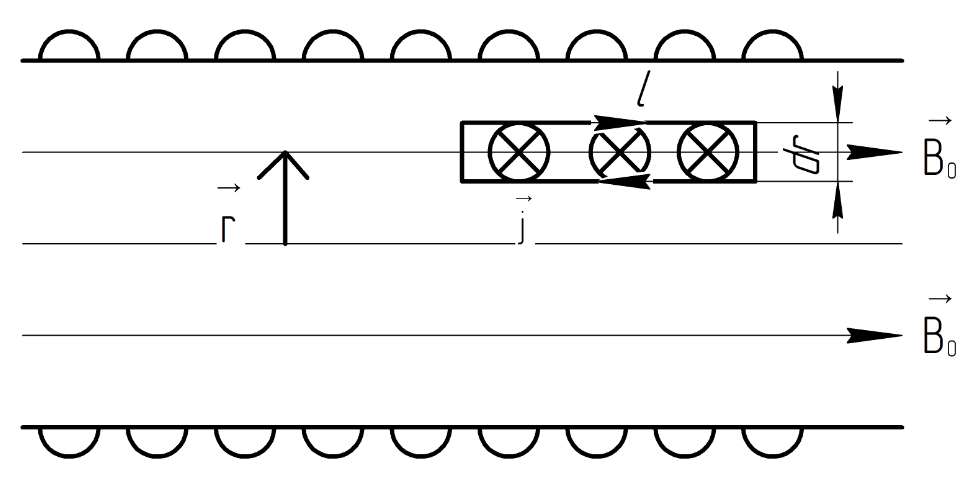Из
рисунка видим:
В теореме о циркуляции получаем:
Таким образом, плотность тока:
Ответ:
.
2.298 Прямой
бесконечно длинный проводник с током
I лежит в плоскости раздела
двух непроводящих сред с магнитными
проницаемостями
и
.
Найти индукцию
магнитного поля во всем пространстве
в зависимости от расстояния r
до провода. Известно, что линии B
являются окружностями с центром на оси
проводника.
Решение. Используем теорему Гаусса для вектора магнитной индукции:
Получаем, что:
Используем теорему о циркуляции вектора :
Граничные
условия для вектора напряжённости
магнитного поля:
Ответ:
.
2.303. Постоянный
магнит имеет вид кольца с узким узором
между полюсами. Средний диаметр кольца
.
Ширина зазора
,
индукция магнитного поля в зазоре
Пренебрегая
рассеянием магнитного поля на краях
зазора, найти модуль напряженности
магнитного поля внутри магнита.
Решение. В условии ничего не сказано о токах проводимости, поэтому мы можем сделать вывод, что они отсутствуют .
Используем теорему о циркуляции вектора :
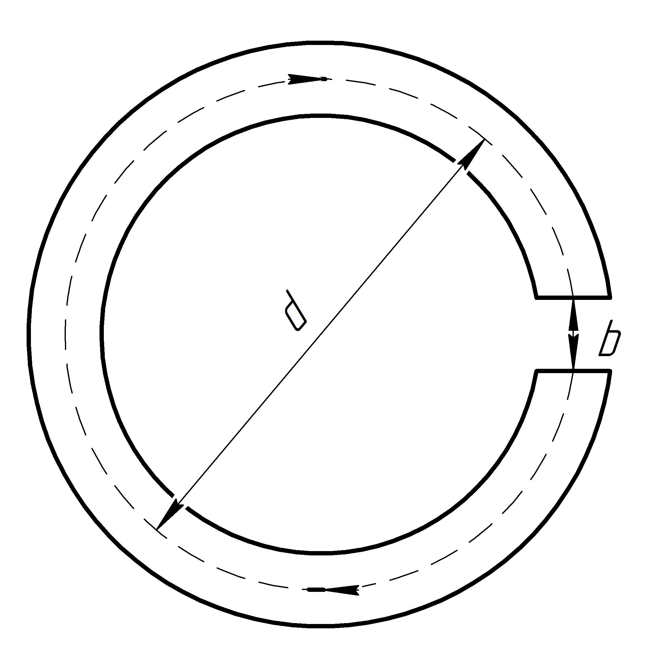После
вычисления интеграла имеем:
Воспользуемся
формулой связи векторов
и
(в зазоре
):
Таким
образом, находим напряжённость магнитного
поля:
Ответ:
2.305. На
железном сердечнике в виде тора со
средним радиусом
имеется обмотка с числом витков
.
В сердечнике сделана поперечная прорезь
ширины
.
При токе
через обмотку индукция магнитного поля
в зазоре
.
Пренебрегая рассеянием магнитного поля
на краях зазора, найти магнитную
проницаемость железа в этих условиях.
Решение. На рисунке представлено поперечное сечение тороида.
Силовыми линиями магнитного поля представленного тороида являются окружности с центром в точке .
Пусть вектора напряжённости магнитного поля имеют направления, показанные на рисунке.
Воспользуемся теоремой о циркуляции вектора :
В качестве
замкнутого контура для вычисления
циркуляции возьмём окружность с радиусом,
равным среднему радиусу тороида и
центром в точке
.
Тогда
на всей окружности, так как она совпадает
с одной из силовых линий.
Так
как магнитное поле внутри тороида и в
небольшом зазоре однородное, то при
движении по силовой линии модуль
напряжённости магнитного поля будет
сохраняться.
Таким образом, из (1) получаем:
Воспользуемся связью между векторами и :
Отсюда получаем выражение для магнитной проницаемости железа:
Рассмотрим более внимательно зазор. Возьмём цилиндр с бесконечно малой высотой, расположенный на границе раздела сред железо-вакуум. Вычислим поток через этот цилиндр.
Для вектора магнитной индукции справедлива теорема Гаусса:
Поток через боковую поверхность равен 0, так как вектор магнитной индукции ⊥ нормали, проведённой к ней в любой точке.
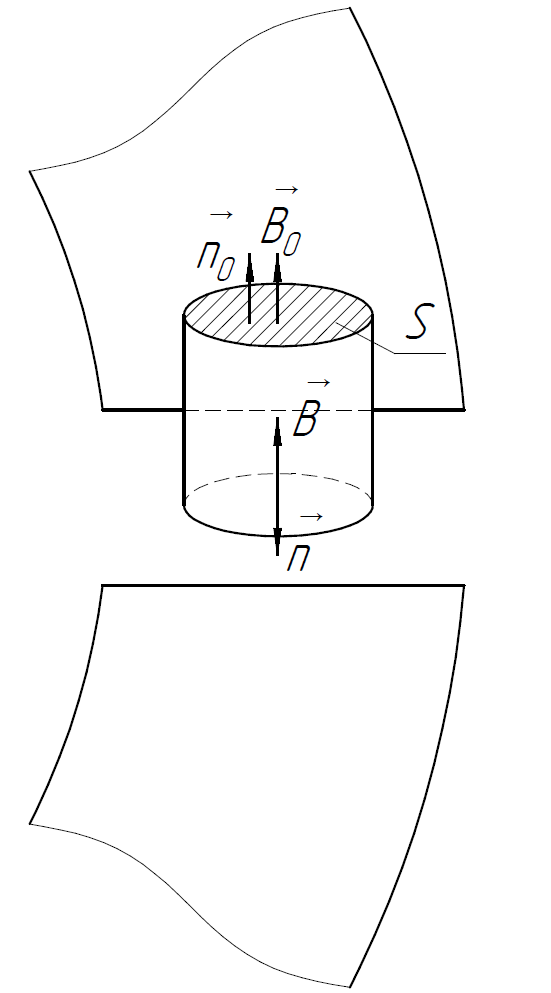Поскольку
направления внешних нормалей к основаниям
разные, необходимо разбить интеграл на
2:
Магнитное поле тороида однородное, следовательно магнитную индукцию можем вынести за знак интеграла. Таким образом, получаем:
Учтём полученный результат в (5):
Так как
,
то приближённо можем записать:
Ответ:
2.307. Тонкое
железное кольцо со средним диаметром
несет на себе обмотку из
витков с током
.
В кольце имеется поперечная прорезь
ширины
.
Пренебрегая рассеянием магнитного поля
на краях зазора, найти магнитную
проницаемость железа в этих условиях.
Решение. Используем теорему о циркуляции :
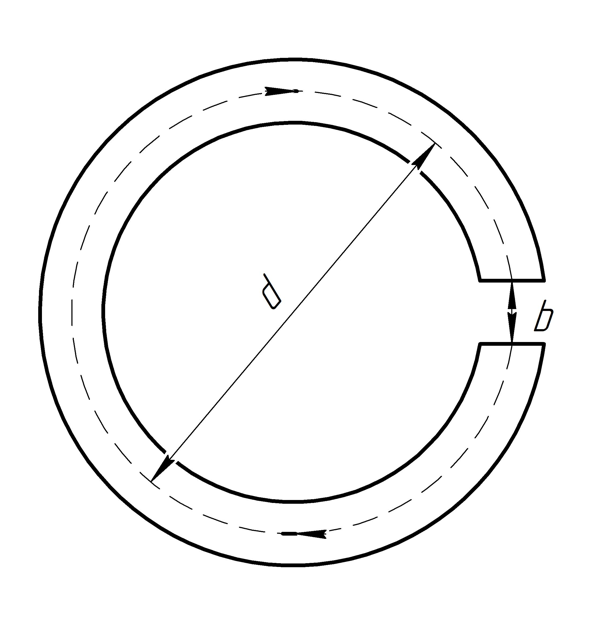Связь
модулей векторов
и
:
Используя (3), перепишем (2):
Так как
,
то приближённо можно записать:
Для модуля вектора получаем:
Исходя из
графика:
.
Отсюда находим магнитную проницаемость:
Ответ:
.