

Министерство общего и профессионального образования
Российской Федерации
ОБНИНСКИЙ ИНСТИТУТ АТОМНОЙ ЭНЕРГЕТИКИ
КАФЕДРА ОБЩЕЙ И СПЕЦИАЛЬНОЙ ФИЗИКИ
В. А. Шакиров
В. А. Панина
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И РЕШЕНИЕ ЗАДАЧ ПО РАЗДЕЛУ
«Электричество» и «Магнетизм»
Обнинск 2024
Шакиров В. А., Панина В. А. Методические указания к решению задач по
Электричеству и Магнетизму
Обнинск, ИАТЭ, 2024
Настоящие пособие с подробным решением задач, предназначенное для самостоятельного изучения задач студентов второго курса на темы – «Электричество» и «Магнетизм» в курсе общей физики. Пособие содержит детально разобранные примеры решения задач в соответствии с действующей программой.
Задачи взяты из сборника задач И. Е. Иродова
(разделы «Электричество» и «Магнетизм»)
Попов М. А. |
Семенов Д.Е. |
Федотов Д. Д. |
Полвонов З. А |
Лабутин Д. А. |
Казимов К. З. |
Обнинский институт атомной энергетики, 2024 г.
Оглавление
Постоянное электрическое поле в вакууме 3
Проводники и диэлектрики в электрическом поле 47
Постоянное магнитное поле. Магнетики 61
Электромагнитная индукция. Уравнения Максвелла 122
Постоянное электрическое поле в вакууме
2.2. Два
одинаковых небольших металлических
шарика с зарядами
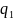 и
и
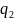 ,
находясь на расстоянии
,
находясь на расстоянии
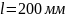 друг от друга, притягиваются с силой
друг от друга, притягиваются с силой
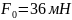 .
После того, как шарики привели в
соприкосновение и опять развели на то
же расстояние
.
После того, как шарики привели в
соприкосновение и опять развели на то
же расстояние
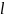 ,
они стали отталкиваться с силой
,
они стали отталкиваться с силой
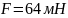 .
Найти
и
.
.
Найти
и
.
Решение. Изначально шарики притягивались, так как были заряжены разноимённо.
П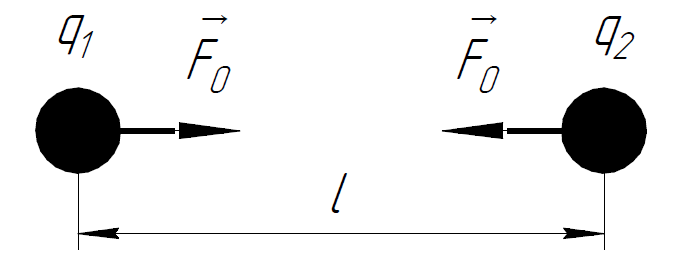 осле
соприкосновения заряд распределился
поровну между шариками, поскольку шарики
одинакового радиуса. Заряд шариков стал
одного знака, и они начали отталкиваться.
осле
соприкосновения заряд распределился
поровну между шариками, поскольку шарики
одинакового радиуса. Заряд шариков стал
одного знака, и они начали отталкиваться.
С ила
взаимодействия двух точечных электрических
зарядов согласно закону Кулона:
ила
взаимодействия двух точечных электрических
зарядов согласно закону Кулона:
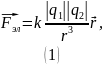
Найдём силу взаимодействия шариков в каждом случае.
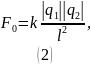
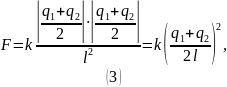
Получили систему из уравнений (2) и (3) для определения и .
Шарики заряжены разноимённо, следовательно из (2):
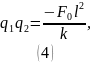
Раскроем скобки в (3):
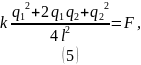
Избавимся от :
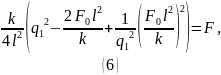
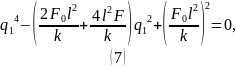
Сделаем замены:
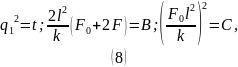
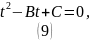
Решая (9), находим:
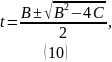
Возвращаемся к заменам:
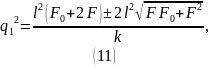
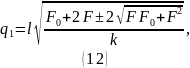
Получаем 4
значения для
:
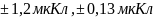 .
.
Из (4):
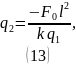
Получаем соответствующие значения для
:
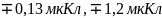 .
.
Ответ:
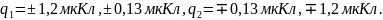
2.8.
Положительный точечный заряд 50 мкКл.
Находится на плоскости
 в точке с радиус вектором
в точке с радиус вектором
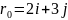 ,
где
,
где
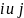 орты осей
орты осей
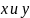 .
Найти напряжённость электрического
поля и её модуль в точке с радиус вектором
.
Найти напряжённость электрического
поля и её модуль в точке с радиус вектором
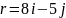 .
.
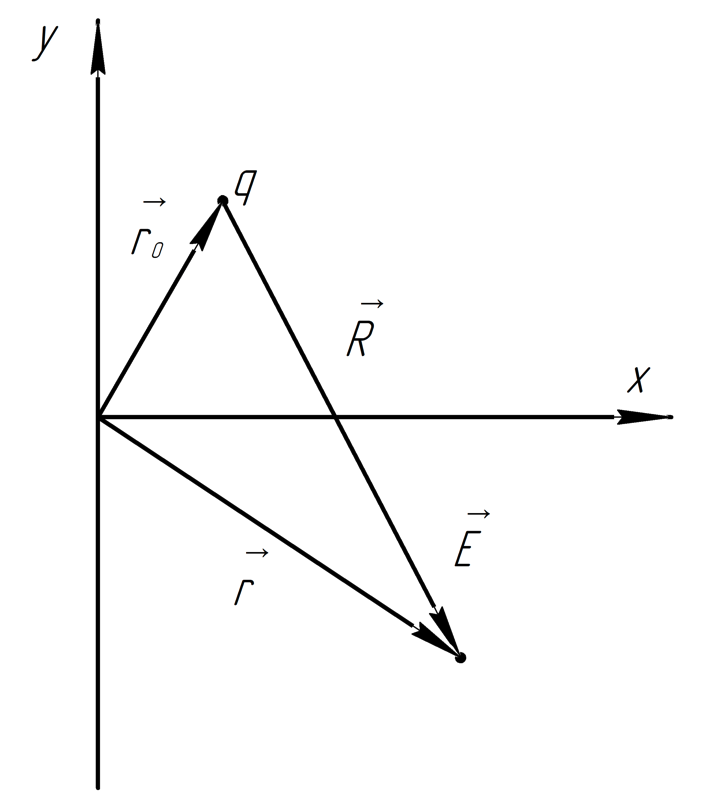 Решение:
Решение:
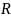 –
расстояние между точками.
–
расстояние между точками.
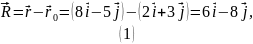
Найдём длину
вектора
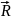 :
:
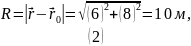
Найдём модуль напряжённости электрического поля.
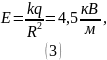
Найдём вектор напряжённости электрического поля.
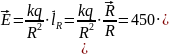
где
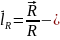 единичный вектор, необходимый для
нахождения напряжённости в векторном
виде.
единичный вектор, необходимый для
нахождения напряжённости в векторном
виде.
Ответ:
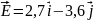 ;
;
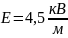 .
.
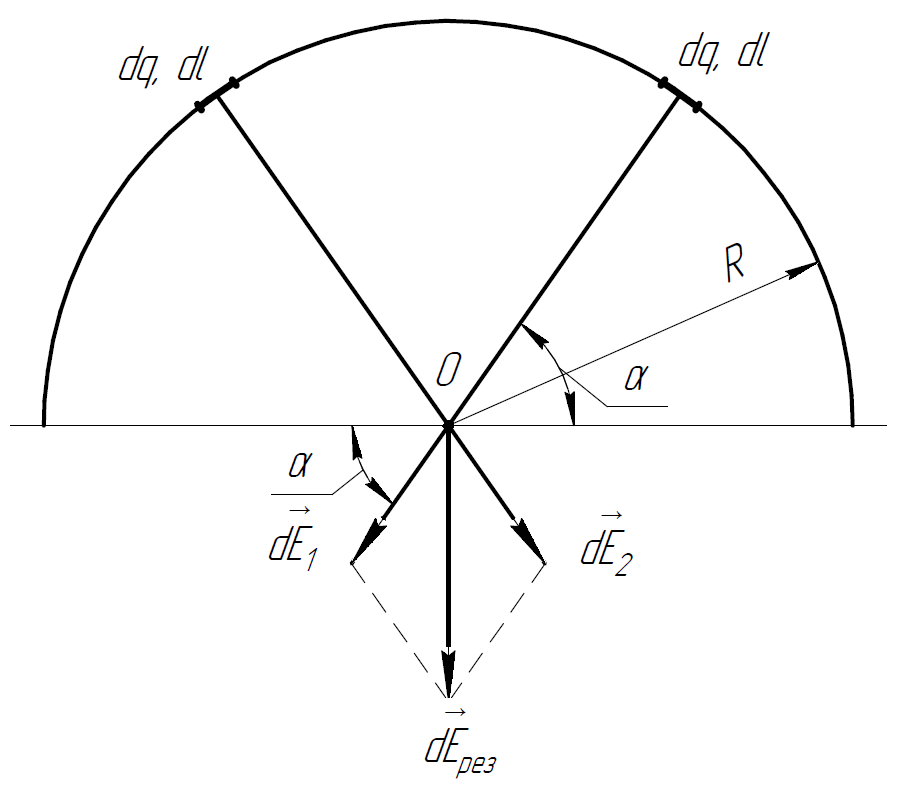
2.11. Тонкое
полукольцо радиуса
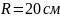 заряжено равномерно зарядом
заряжено равномерно зарядом
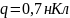 .
Найти модуль напряжённости электрического
поля в центре кривизны этого полукольца.
.
Найти модуль напряжённости электрического
поля в центре кривизны этого полукольца.
Решение.
Разобьём полукольцо на бесконечно малые
участки длины
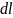 .
Каждому такому участку соответствует
заряд
.
Каждому такому участку соответствует
заряд
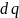 .
.
Для упрощения геометрической составляющей задачи выберем на полукольце 2 симметрично расположенных отрезка.
Заряд можно считать точечным.
Проведём
вектора напряженности электрического
поля, создаваемые этими отрезками. Так
как заряд
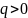 ,
то они направлены от точечных зарядов.
,
то они направлены от точечных зарядов.
Для нахождения
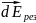 воспользуемся принципом суперпозиции
для вектора
воспользуемся принципом суперпозиции
для вектора
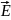 :
:
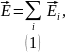
Напряжённость электрического поля, создаваемая точечным электрическим зарядом:
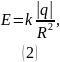
Найдём
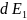 и
и
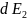 .
.
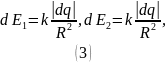
В силу
симметрии вектор
направлен вертикально вниз, следовательно
для нахождения
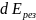 складываем вертикальные составляющие
векторов
складываем вертикальные составляющие
векторов
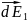 и
и
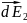 .
Также в силу симметрии они одинаковы.
.
Также в силу симметрии они одинаковы.
Введём угол
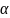 между горизонталью и вектором
.
между горизонталью и вектором
.
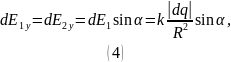
 Линейная
плотность заряда полукольца:
Линейная
плотность заряда полукольца:
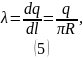
Отсюда выразим
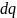 :
:
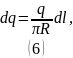
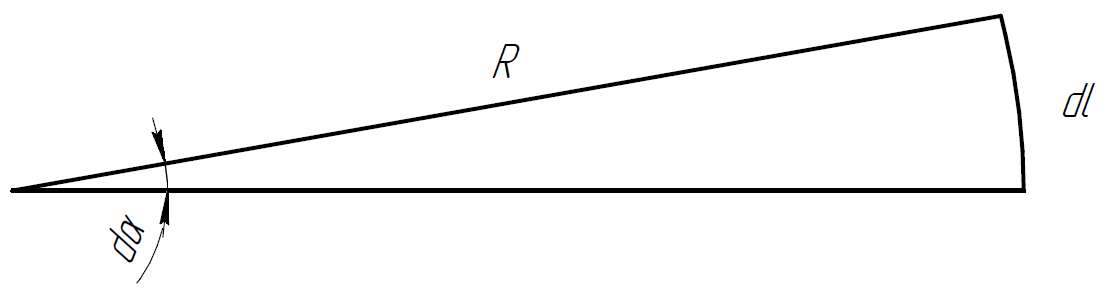
Из рисунка
можно заметить, что
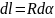 .
.
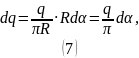
Можем найти :
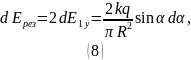
Найдём напряжённость электрического поля, создаваемую в центре кривизны полукольца всеми участками:
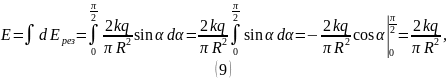
Ответ:
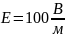 .
.
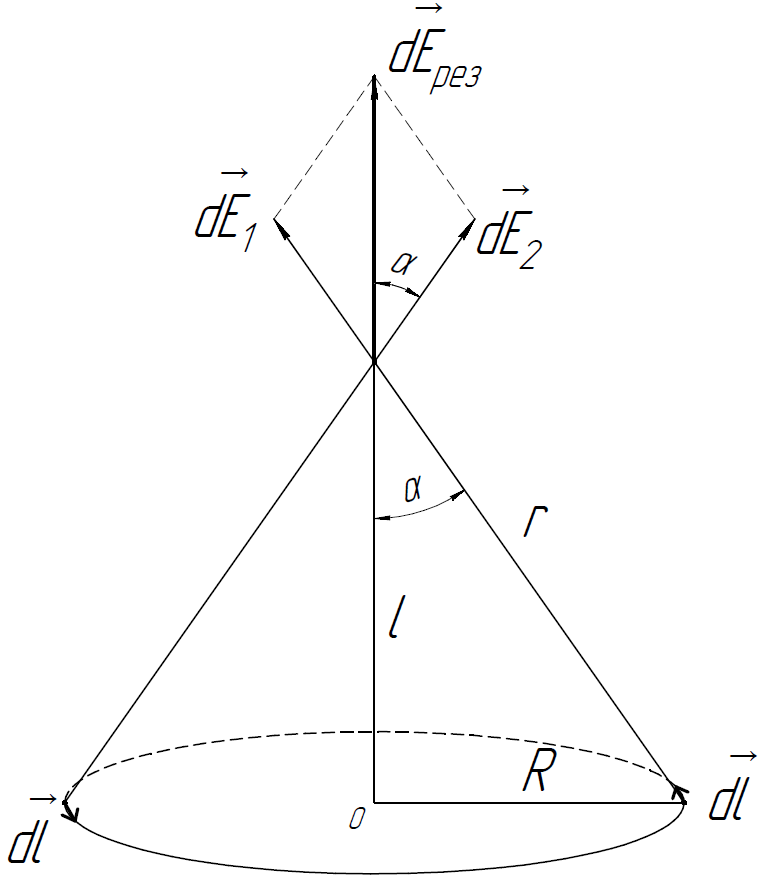 2.12.
Кольцо радиуса
из тонкой проволоки имеет заряд
2.12.
Кольцо радиуса
из тонкой проволоки имеет заряд
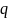 .
Найти модуль напряжённости электрического
поля на оси кольца как функцию расстояния
от его центра. Исследовать
.
Найти модуль напряжённости электрического
поля на оси кольца как функцию расстояния
от его центра. Исследовать
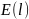 при
при
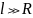 .
Определить максимальное значение
напряжённости и соответствующее
расстояние
.
Определить максимальное значение
напряжённости и соответствующее
расстояние
Решение.
Пусть кольцо
имеет заряд
и длину
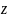 .
Разобьём кольцо на бесконечно малые
участки длины
.
Разобьём кольцо на бесконечно малые
участки длины
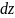 (таким участкам соответствует заряд
).
Далее выберем симметричные точки на
кольце (для упрощения геометрической
составляющей задачи).
можно рассматривать как точечный заряд.
(таким участкам соответствует заряд
).
Далее выберем симметричные точки на
кольце (для упрощения геометрической
составляющей задачи).
можно рассматривать как точечный заряд.
В задаче
ничего не сказано о знаке заряда. Для
определённости предположим, что
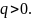
Проведём
вектора напряжённости
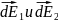 (направлены от точечных зарядов, так
как заряды положительные)
(направлены от точечных зарядов, так
как заряды положительные)
Воспользуемся принципом суперпозиции: Результирующий вектор напряжённости равен векторной сумме векторов напряжённости полей, создаваемых каждым зарядом:
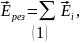
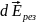 направлен вертикально вверх, поэтому
суммировать будем лишь вертикальные
составляющие
направлен вертикально вверх, поэтому
суммировать будем лишь вертикальные
составляющие
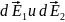 .
.
Напряжённость электрического поля, создаваемого точечным зарядом:
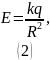
В нашем случае складываем лишь вертикальные проекции.
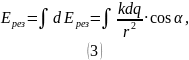
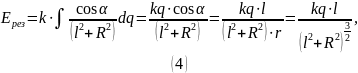
При кольцо приближённо можно считать точечным зарядом.
Соответственно в выражении (4) пропадут все радиусы.
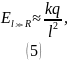
Найдём
экстремум функции
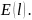
Производная в точке экстремума должна быть равна нулю.
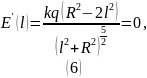
Решая данное уравнение, находим точку экстремума:
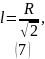
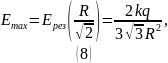
Ответ:
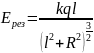 . При
:
. При
:
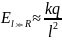 .
.
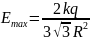 при
при
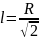 .
.
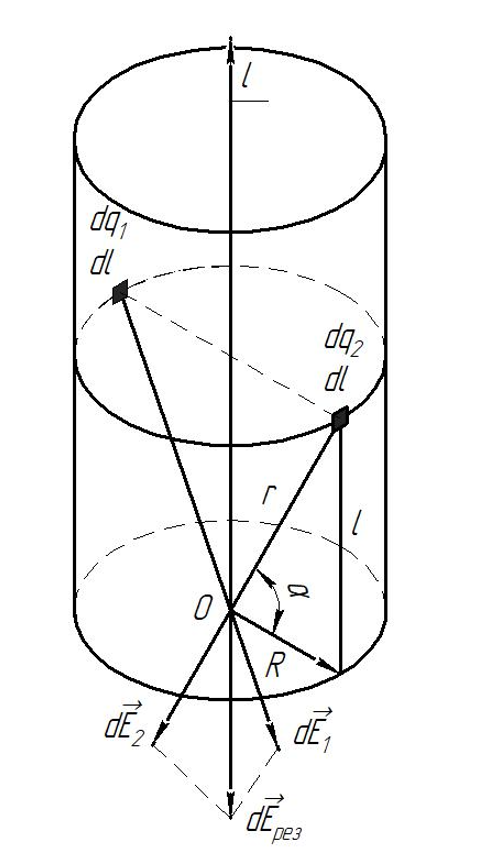
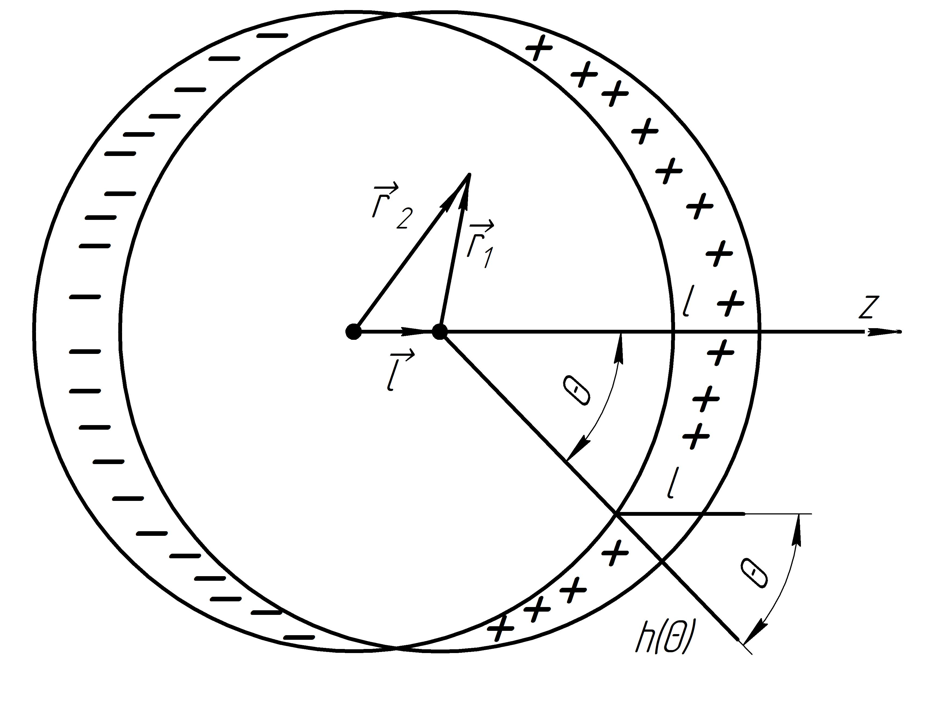
2.13. Полубесконечный круглый цилиндр радиуса R заряжен равномерно по поверхности так, что на единицу его длины приходится заряд λ. Найти напряженность электрического поля в центре основания цилиндра.
Решение. Разобьем цилиндр на бесконечное множество бесконечно малых колец с зарядом и шириной . Выберем две симметричные точки на выбранном кольце (симметричные ради упрощения геометрической составляющей части задачи). Точки будем считать точечными зарядами.
Линейная плотность заряда:
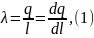
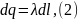
В задаче ничего не сказано про знак заряда, поэтому для определённости будем считать, что .
Проведем вектора напряженности (будут направлены от точечных зарядов, т.к. ).
Воспользуемся принципом суперпозиции для вектора напряжённости электрического поля:
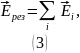
 Так
как
Так
как
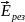 направлен вертикально вниз, для его
нахождения будем складывать только
вертикальные составляющие векторов:
направлен вертикально вниз, для его
нахождения будем складывать только
вертикальные составляющие векторов:
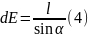
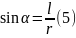
Напряженность электрического поля для точечного заряда:
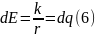
В нашем случае (складываем лишь вертикальные составляющие):
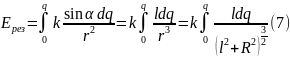
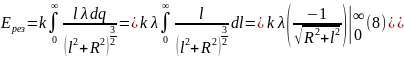
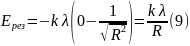
Ответ:
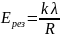 .
.
2.14. Найти
напряженность электрического поля в
центре полусферы, заряженной равномерно
с поверхностной плотностью
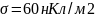 .
.
Решение. Для определённости предположим, что .
Площадь
поверхности сферы равна
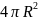 ,
следовательно площадь поверхности
полусферы равна
,
следовательно площадь поверхности
полусферы равна
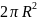 .
.
Разобьем
полусферу на бесконечно малые части,
имеющие заряд
и площадь
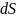 .
Выбираем две части (из соображений
симметрии берем их симметричными
относительно оси
.
Выбираем две части (из соображений
симметрии берем их симметричными
относительно оси
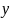 ,
это упростит геометрическую составляющую
задачи).
,
это упростит геометрическую составляющую
задачи).
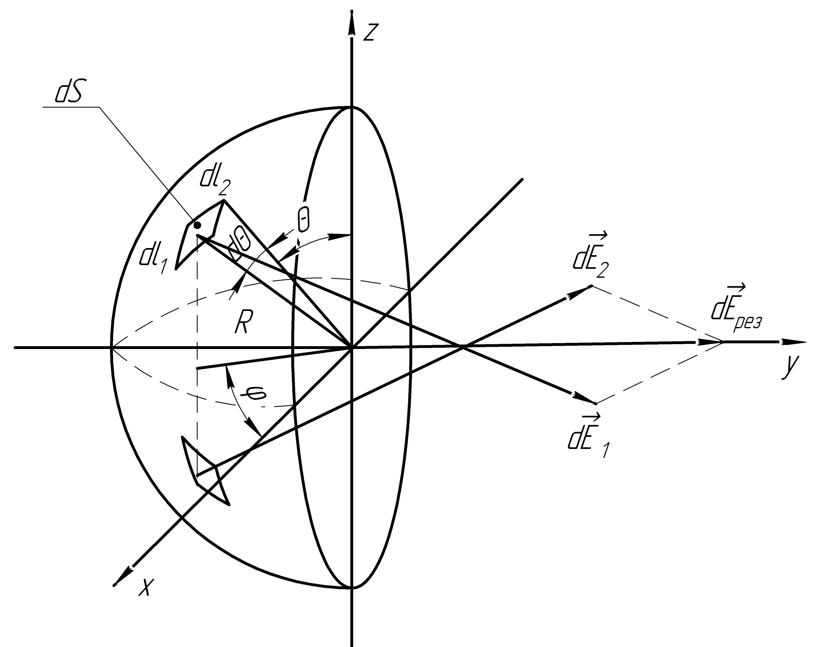 Часть
имеет стороны
Часть
имеет стороны
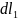 и
и
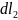 .
Перейдем к сферической системе координат.
.
Перейдем к сферической системе координат.
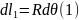
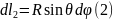
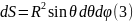
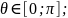
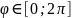
От точечных
зарядов проведем вектора напряженности
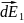 и
и
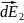 .
Они направлены от точечных зарядов,
т.к.
.
.
Они направлены от точечных зарядов,
т.к.
.
Воспользуемся принципом суперпозиции для вектора напряжённости электрического поля:
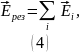
Результирующий вектор напряженности направлен по горизонтали. Для его нахождения суммируем лишь горизонтальные составляющие.
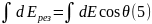
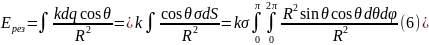
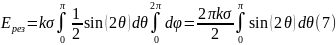
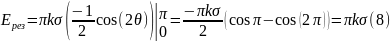
В итоге получаем:
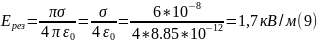
Ответ:
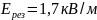 .
.
2.16. Система
состоит из тонкого заряженного
проволочного кольца радиуса
и очень длинной равномерно заряженной
нити, расположенной по оси кольца так,
что один из её концов совпадает с центром
кольца. Кольцо имеет заряд
.
На единицу длины нити приходится заряд
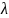 .
Найти силу взаимодействия кольца и
нити.
.
Найти силу взаимодействия кольца и
нити.
Решение.
Пусть кольцо
имеет заряд
и длину
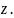 Разобьём кольцо на бесконечно малые
части, имеющих длину
и заряд
.
Возьмём две симметрично расположенные
точки для упрощения геометрической
составляющей задачи.
Разобьём кольцо на бесконечно малые
части, имеющих длину
и заряд
.
Возьмём две симметрично расположенные
точки для упрощения геометрической
составляющей задачи.
Так как про знак заряда кольца ничего не сказано, для определённости предположим, что
Проведём
вектора напряжённости. Так как
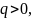 то вектора направлены от точечных
зарядов.
то вектора направлены от точечных
зарядов.
Используем принцип суперпозиции для вектора напряжённости для определения .
направлен вертикально вверх, следовательно можем суммировать только вертикальные составляющие векторов
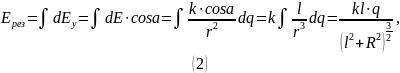
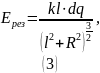
По определению напряжённости электрического поля:
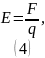
Тогда сила,
действующая на участок нити длины
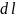 .
.
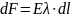
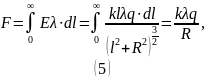
Ответ:
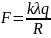 .
.
2.17. Тонкое
непроводящее кольцо радиуса
заряжено с линейной плотностью
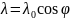 ,
где
,
где
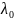 – постоянная,
– постоянная,
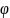 – азимутальный угол. Найти модуль
напряжённости электрического поля в
центре кольца.
– азимутальный угол. Найти модуль
напряжённости электрического поля в
центре кольца.
 Решение.
Решение.
Разобьём кольцо на бесконечное число частей длины .
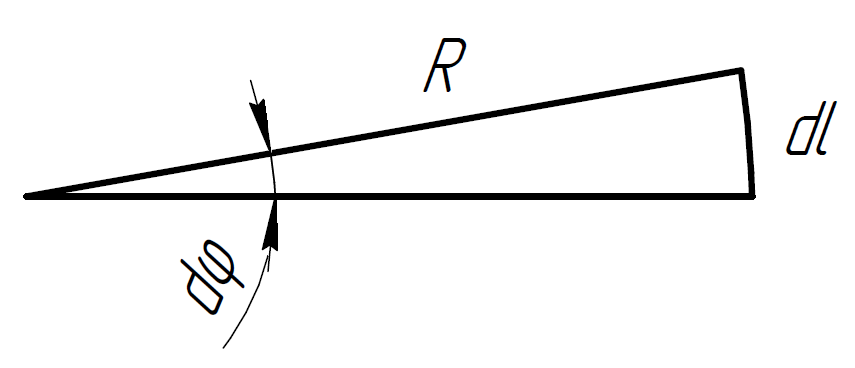 Каждый
такой отрезок создаёт в центре кольца
напряжённость электрического поля
Каждый
такой отрезок создаёт в центре кольца
напряжённость электрического поля
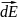 :
:
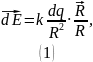 Тогда
модуль напряжённости электрического
поля:
Тогда
модуль напряжённости электрического
поля:
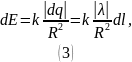
Из
рисунка можно увидеть, что
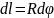 .
.
С учётом этого выражение для напряжённости примет вид:
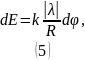
Угол
будем отсчитывать от оси
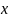 против часовой стрелки.
против часовой стрелки.
Найдём проекции напряжённости на оси и :
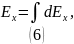
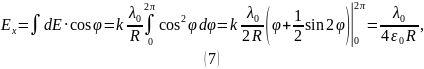
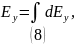
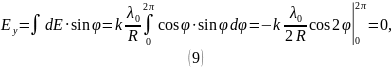
Таким образом, суммарная напряжённость электрического поля в центре кольца:
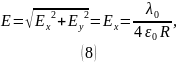
Ответ:
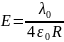 .
.
2.18. Находящийся
в вакууме тонкий прямой стержень длины
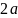 заряжен равномерно зарядом
.
Найти модуль напряженности электрического
поля как функцию расстояния r
от центра стержня до точки прямой,
заряжен равномерно зарядом
.
Найти модуль напряженности электрического
поля как функцию расстояния r
от центра стержня до точки прямой,
А) перпендикулярной стержню и проходящей через его центр,
Б) совпадающей
с осью стержня, если
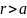 .
.
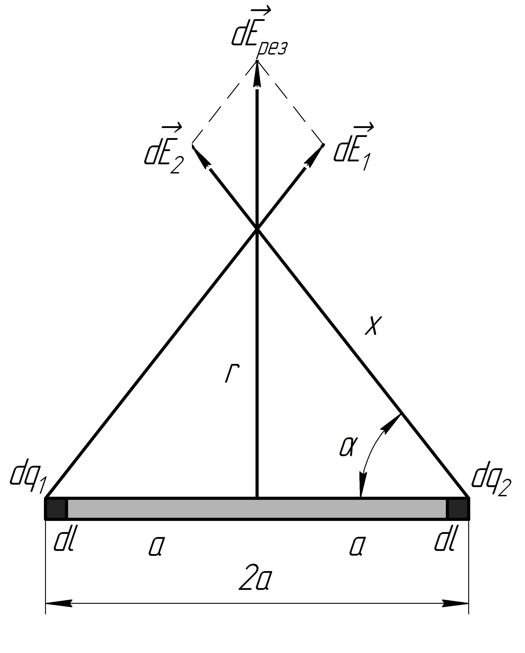 Исследовать
полученное выражение при
Исследовать
полученное выражение при
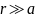 .
.
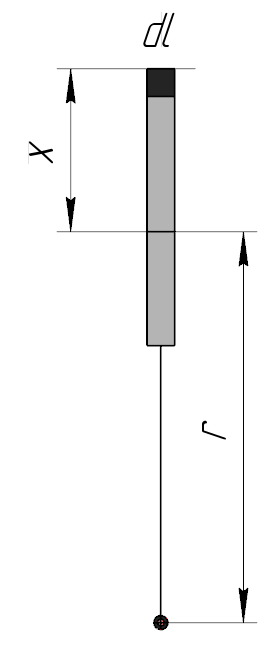
Решение. а)
Разобьем стержень на бесконечно малые части, имеющие заряд и длину . Возьмем два симметричных точечных заряда (чтобы упростить геометрическую составляющую задачи).
Линейная плотность заряда равномерно заряженного стержня:
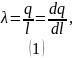
Тогда на бесконечно малом участке содержится заряд:
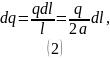
Проведем вектора напряженности электрического поля. Предположим, что . Вектора направлены от точечных зарядов.
Воспользуемся принципом суперпозиции для вектора :
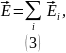
Результирующий вектор напряженности направлен вертикально вверх. Для его нахождения будем суммировать лишь вертикальные составляющие векторов.
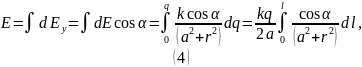
Из рисунка можем заметить:
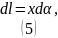
Подставим (5) в (4):
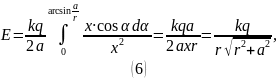
 б)
б)
В данном случае для напряжённости электрического поля имеем:
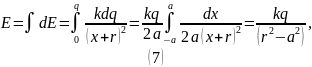
В обоих
случаях при
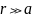 :
:
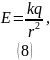
Ответ: а)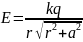 ;
б)
;
б)
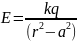 .
.
2.19. Длинная прямая равномерно заряженная нить имеет заряд λ на единицу длины. Найти модуль и направление электрического поля в точке, которая отстоит от нити на расстояние y и находится на перпендикуляре к нити, проходящем через один из её концов.
Решение.
Разобьем нить на бесконечно большое
количество бесконечно малых частей,
имеющих заряд
и длину
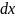 .
Выберем одну точку для построения
(точечный заряд).
.
Выберем одну точку для построения
(точечный заряд).
Проведем
вектор напряженности от нашего точечного
заряда (для определенности будем считать,
что
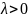 ).
).
Из рисунка видим, что:
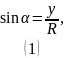
Для нахождения модуля напряжённости электрического поля потребуется найти проекции вектора на оси и .
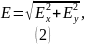
Из определения линейной плотности заряда:
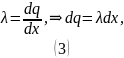
Из рисунка видно, что:
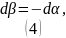
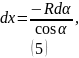
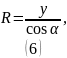
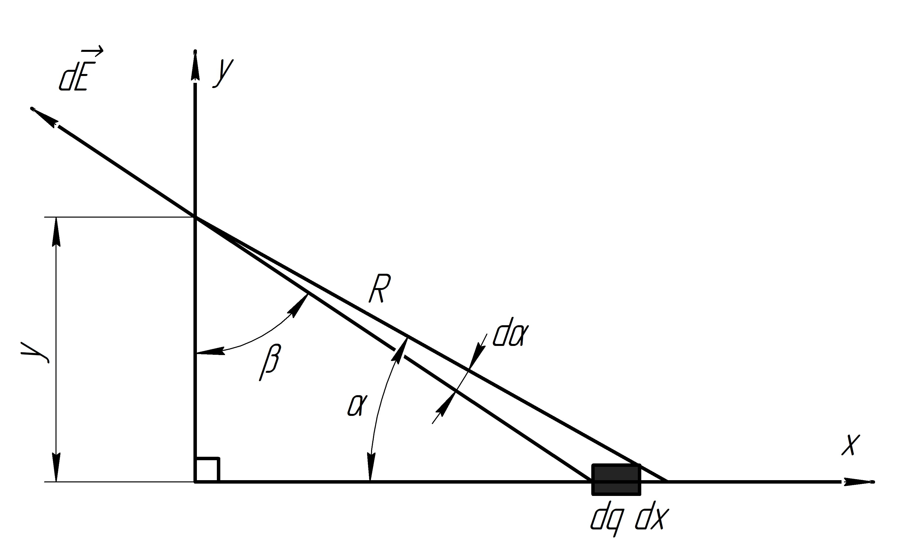 Найдем
проекцию вектора
на ось
:
Найдем
проекцию вектора
на ось
:
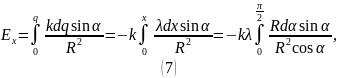
С помощью (6) получаем:
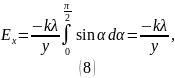
Найдем проекцию вектора на ось :
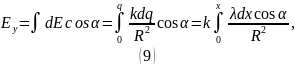
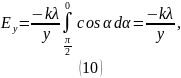
Таким образом, модуль вектора напряженности равен:
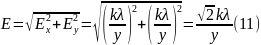
Ответ:
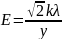 .
.
2.21. Сфера
радиуса
 заряжена с поверхностной плотностью
заряжена с поверхностной плотностью
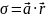 ,
где
,
где
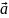 –
постоянный вектор,
–
постоянный вектор,
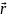 –
радиус вектор точки сферы относительно
её центра. Найти напряжённость
электрического поля в центре сферы.
–
радиус вектор точки сферы относительно
её центра. Найти напряжённость
электрического поля в центре сферы.
Решение. Разделим поверхность сферы на малые участки площадью , имеющие заряд (каждую площадку можно считать точечным зарядом).
Рассмотрим симметрично расположенные относительно друг друга заряды.
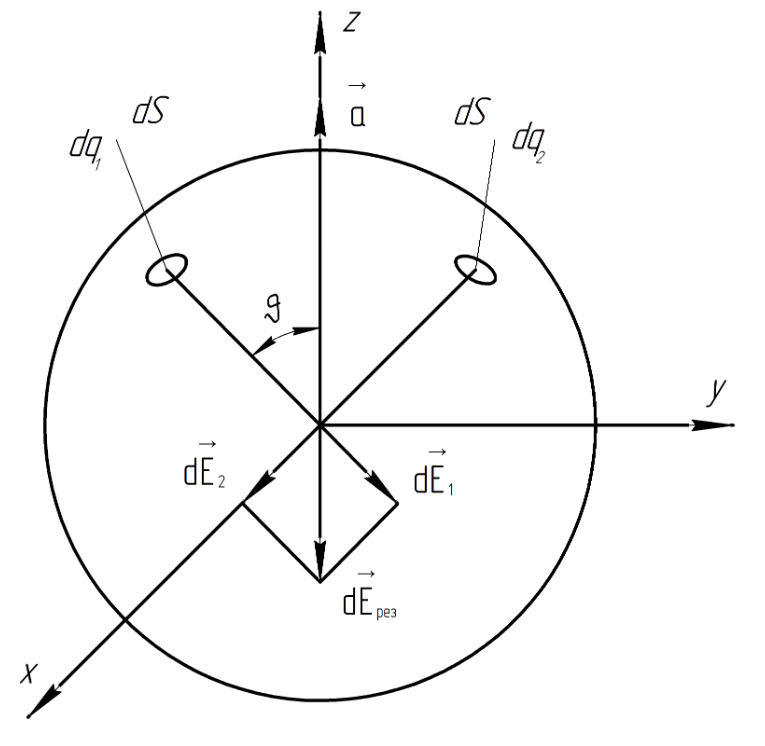 Предположим,
что
.
Проведём вектора напряжённости. Они
направлены от точечных зарядов.
Предположим,
что
.
Проведём вектора напряжённости. Они
направлены от точечных зарядов.
Положение
каждого точечного заряда в сферической
системе координат характеризуется
радиусом
и
углами
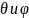 .
.
Воспользуемся принципов суперпозиции для вектора напряжённости электрического поля:
Так как
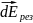 направлен вертикально вниз, то для
нахождения результирующей напряжённости
от всех участков достаточно просуммировать
только вертикальные составляющие.
направлен вертикально вниз, то для
нахождения результирующей напряжённости
от всех участков достаточно просуммировать
только вертикальные составляющие.
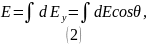
Из определения поверхностной плотности заряда:
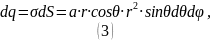
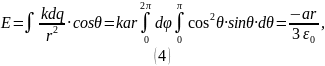
Учитывая знак минус, делаем вывод, что направлен вертикально вверх:
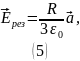
Ответ:
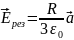 .
.
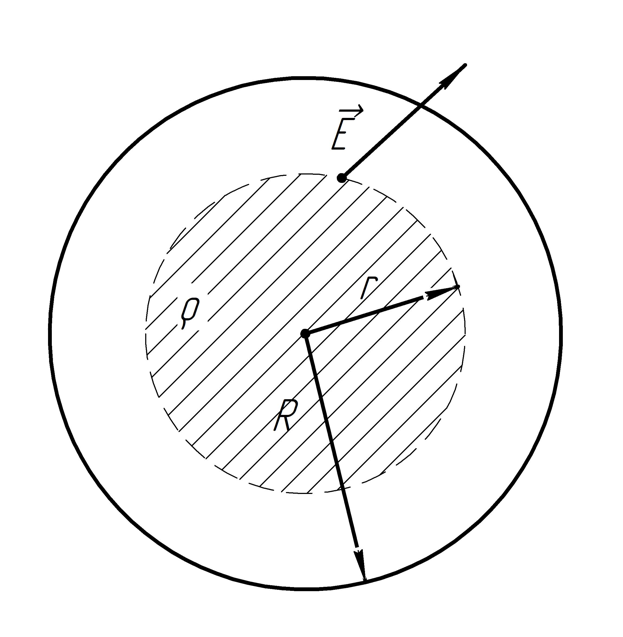
2.22.
Поверхностная плотность заряда на сфере
радиуса
зависит от полярного угла
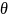 как
как
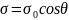 ,
где
,
где
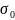 - положительная постоянная. Показать,
что такое распределение заряда можно
представить как результат малого сдвига
относительно друг друга двух равномерно
заряженных шаров радиуса
,
заряды которых одинаковы по модулю и
противоположны по знаку. Воспользовавшись
этим представлением, найти напряженность
электрического поля внутри данной
сферы.
- положительная постоянная. Показать,
что такое распределение заряда можно
представить как результат малого сдвига
относительно друг друга двух равномерно
заряженных шаров радиуса
,
заряды которых одинаковы по модулю и
противоположны по знаку. Воспользовавшись
этим представлением, найти напряженность
электрического поля внутри данной
сферы.
 Решение.
Решим вначале вспомогательную задачу,
найдем напряженность внутри однородно
заряженного шара.
Решение.
Решим вначале вспомогательную задачу,
найдем напряженность внутри однородно
заряженного шара.
Для нахождения напряжённости электрического поля воспользуемся теоремой Гаусса:
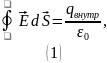 Выберем
поверхность в виде сферы, с радиусом
меньше радиуса шара. Из соображений
симметрии следует, что на этой поверхности
вектор
перпендикулярен поверхности, и по модулю
постоянен.
Выберем
поверхность в виде сферы, с радиусом
меньше радиуса шара. Из соображений
симметрии следует, что на этой поверхности
вектор
перпендикулярен поверхности, и по модулю
постоянен.
Тогда в
теореме Гаусса с такой поверхностью
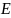 можно вынести за интеграл:
можно вынести за интеграл:
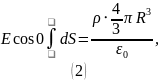
После упрощения получаем следующее выражение для модуля напряжённости:
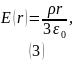
В векторном виде:
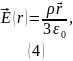
 Далее
докажем, что наложение двух однородно
заряженных шаров с плотностями зарядов
Далее
докажем, что наложение двух однородно
заряженных шаров с плотностями зарядов
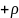 и
и
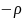 ,
с очень малым сдвигом центров даем
поверхностное распределение зарядов
.
,
с очень малым сдвигом центров даем
поверхностное распределение зарядов
.
Поверхность получившиеся фигуры при очень малом сдвиге центров можно считать сферой.
В нашей задаче толщина заряженного слоя изменяется. В направлении, определяемым углом , толщина определяется по формуле:
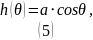 где
где
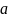 – расстояние между центрами.
– расстояние между центрами.
И тогда объемную плотность заряда можно выразить следующим образом
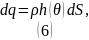
Так как
толщина зависит от угла
,
как и поверхностная плотность заряда
(по условию задачи), то заряд, распределенный
по объему, можно считать распределенным
по поверхности с плотностью
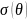 .
.
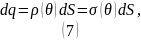
Приравнивая (6) и (7), получаем:
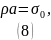
Для произвольной
точки в области пересечения шаров можно
записать
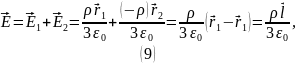
где
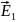 и
и
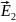 – вектора напряженностей для положительно
заряженных шаров,
– вектора напряженностей для положительно
заряженных шаров,
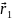 и
и
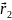 - радиус-векторы, проведенные из центров
шаров в точку вычисления напряженностей.
- радиус-векторы, проведенные из центров
шаров в точку вычисления напряженностей.
Ответ:
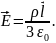
2.23. Найти
напряжённость электрического поля в
центре шара радиуса
,
объёмная плотность заряда которого
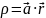 ,
где
– постоянный вектор,
– радиус-вектор относительно центра
шара.
,
где
– постоянный вектор,
– радиус-вектор относительно центра
шара.
Решение. По условию задана объёмная плотность заряда шара:
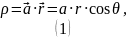
 Таким
образом, имеем следующее распределение
заряда внутри шара:
Таким
образом, имеем следующее распределение
заряда внутри шара:
Выберем за
направление вектора
горизонтальное и проведём по
ось
.
Для бесконечно малого заряда
в объёме
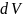 :
:
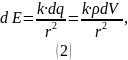
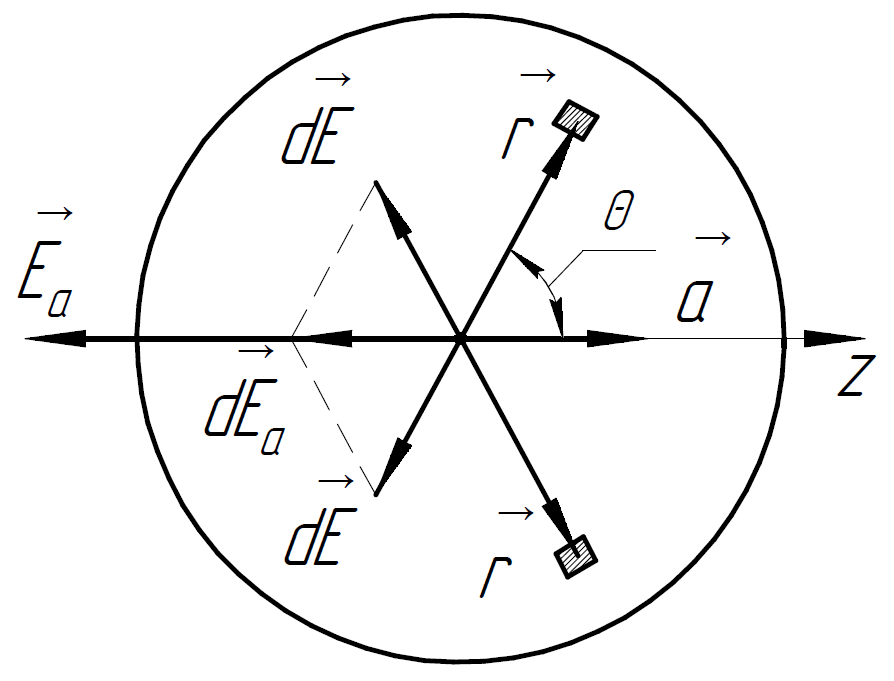 Рассмотрим
также расположенный симметрично
относительно оси
заряд
.
Суммарная напряжённость электрического
поля от данных двух зарядов направлена
вдоль оси
(в отрицательную сторону).
Рассмотрим
также расположенный симметрично
относительно оси
заряд
.
Суммарная напряжённость электрического
поля от данных двух зарядов направлена
вдоль оси
(в отрицательную сторону).
Следовательно, для её нахождения можно суммировать только проекции напряжённостей от зарядов на ось , то есть:
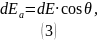
Преобразуем
выражение для суммарной напряжённости
с учётом выражения для объёма
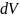 в сферической системе координат:
в сферической системе координат:
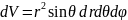 .
.
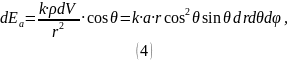
Проинтегрировав данное выражение, найдём напряжённость электрического поля относительно вектора :
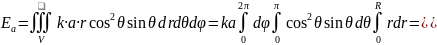
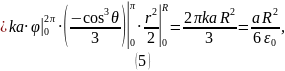
Так как
и
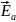 направлены противоположно друг другу,
то можем записать:
направлены противоположно друг другу,
то можем записать:
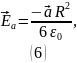
Ответ:
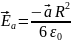 .
.
2.25. Две
длинные параллельные нити равномерно
заряжены, каждая с линейной плотностью
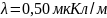 .
Расстояние между нитями
.
Расстояние между нитями
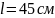 .
Найти максимальное значение напряжённости
электрического поля в плоскости симметрии
этой системы.
.
Найти максимальное значение напряжённости
электрического поля в плоскости симметрии
этой системы.
Решение. Найдём модуль напряжённости электрического поля, создаваемого одной нитью на расстоянии от неё.
Равномерно заряженная нить создаёт вокруг себя аксиально симметричное электрическое поле, следовательно на любой цилиндрической поверхности модуль напряжённости будет одинаковый. Так как , то направлен от нити.
П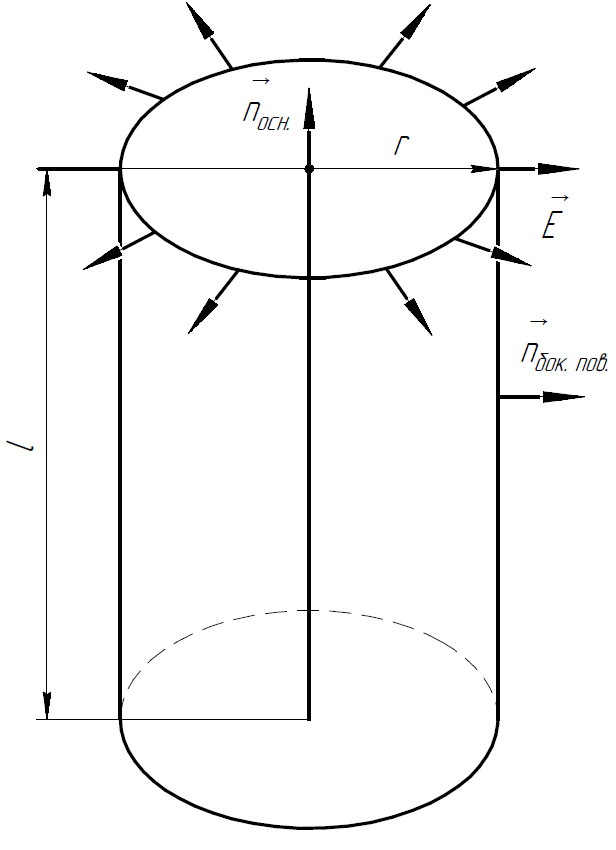 рименим
теорему Гаусса. В качестве гауссовой
поверхности выберем цилиндр радиуса
.
рименим
теорему Гаусса. В качестве гауссовой
поверхности выберем цилиндр радиуса
.
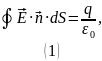
Поверхность цилиндра состоит из боковой поверхности и двух оснований. Пользуясь этим, разобьём интеграл на 2:
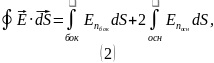
Воспользуемся определением проекции вектора на направление:
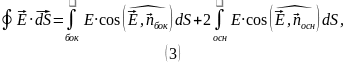
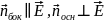 ,
следовательно
,
следовательно
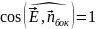 ,
,
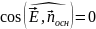 .
.
Так как модуль на выбранном цилиндре одинаков, то можем вынести его за знак интеграла и вычислить поток через цилиндр:
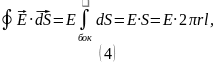
Вернёмся к теореме Гаусса:
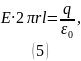
Выразим отсюда и воспользуемся определением линейной плотности заряда:
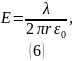
Рассмотрим теперь 2 нити. Расположим их перпендикулярно рисунку.
Р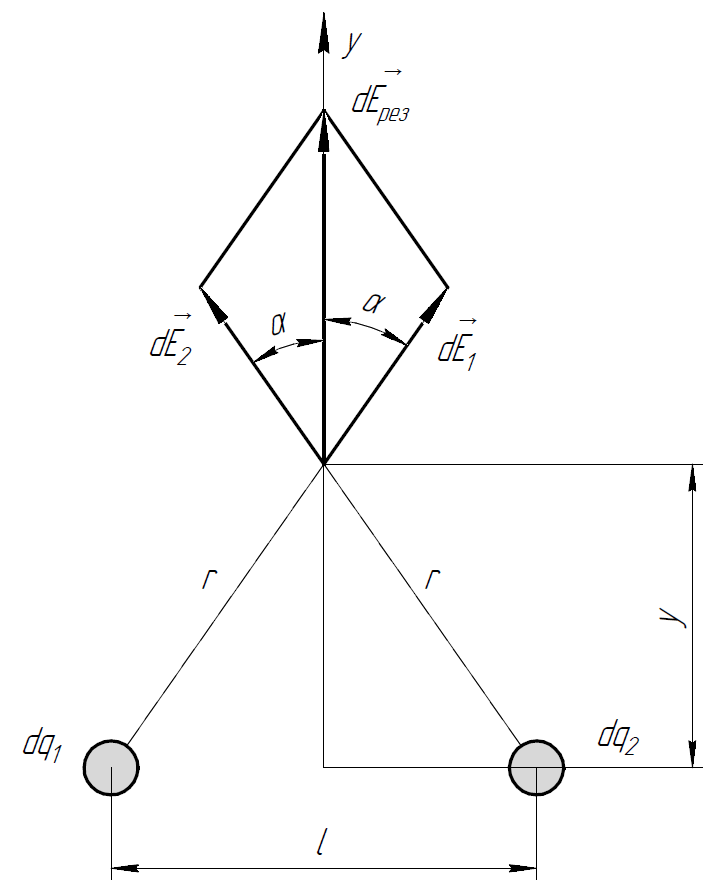 азделим
нити на бесконечно малые части. Каждая
такая часть имеет заряд
.
Выберем 2 точки, расположенные симметрично
относительно вертикальной оси, чтобы
упростить геометрическую составляющую
задачи.
азделим
нити на бесконечно малые части. Каждая
такая часть имеет заряд
.
Выберем 2 точки, расположенные симметрично
относительно вертикальной оси, чтобы
упростить геометрическую составляющую
задачи.
Воспользовавшись принципом суперпозиции для , можем найти найдём направление – он направлен вертикально вверх.
Сложив
напряжённости от всех бесконечно малых
участков, получим, что
также направлен вертикально вверх, а
все горизонтальные составляющие векторов
 взаимно компенсируются.
взаимно компенсируются.
Для нахождения
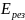 будем складывать вертикальные составляющие
напряжённостей от обеих нитей:
будем складывать вертикальные составляющие
напряжённостей от обеих нитей:
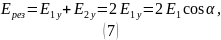
Воспользуемся
напряжённостью электрического поля
для одной нити, а также найдём
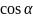 из рисунка:
из рисунка:
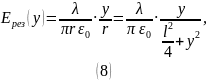
Найдём
экстремум функции
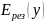 .
Для этого вычислим производную:
.
Для этого вычислим производную:
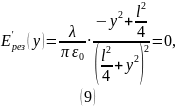
Решая данное уравнение, находим точку экстремума – точку максимума.
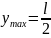
Подставляя
данное значение в (8), находим
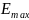 :
:
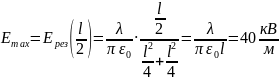
Ответ:
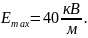
2.29. Имеется
аксиально-симметричное электрическое
поле, напряжённость которого зависит
от расстояния
до его оси как
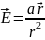 ,
где
- постоянная. Найти заряд внутри сферы
радиуса
с центром на оси этого поля.
,
где
- постоянная. Найти заряд внутри сферы
радиуса
с центром на оси этого поля.
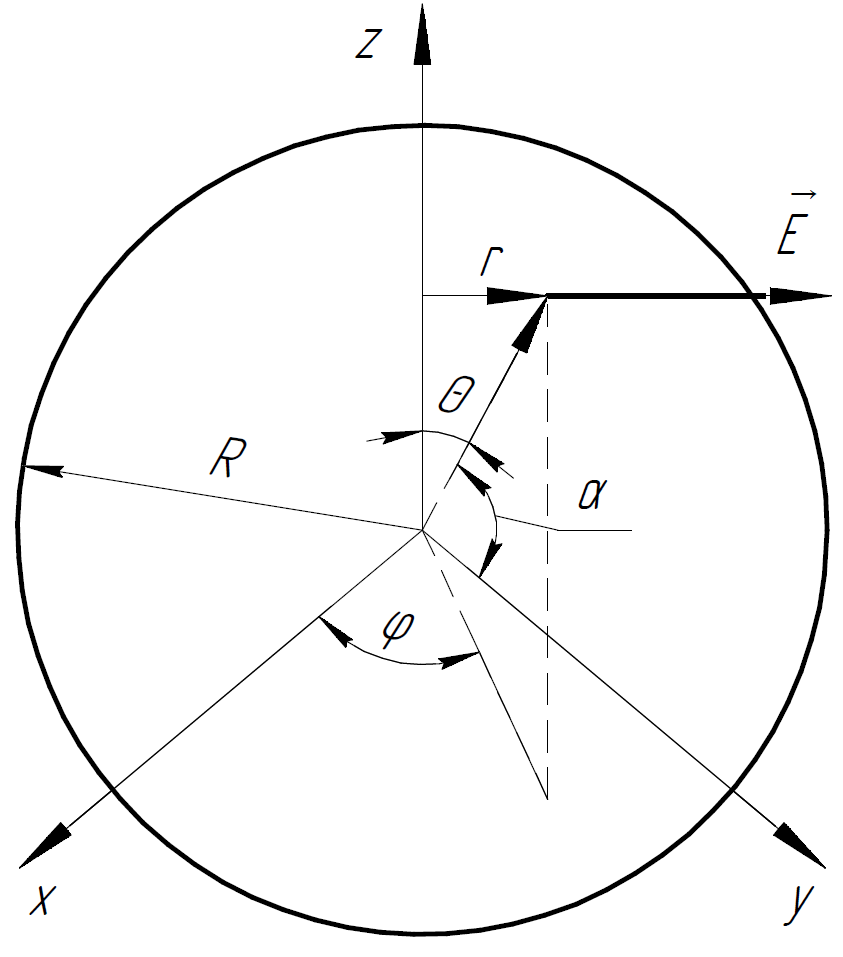 Решение.
С помощью теоремы Остроградского-Гаусса
можем найти заряд, помещённый внутри
замкнутой поверхности:
Решение.
С помощью теоремы Остроградского-Гаусса
можем найти заряд, помещённый внутри
замкнутой поверхности:
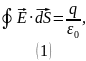
Так как требуется найти заряд внутри сферы радиуса , то именно её мы выберем в качестве замкнутой поверхности.
Для начала
найдём поток вектора
через сферу. Интеграл вычислим в
сферической системе координат (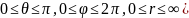 .
.
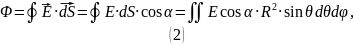
Модуль напряжённости электрического поля:
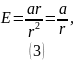
Из рисунка
можно увидеть, что
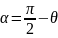 ,
,
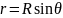 .
.
Тогда поток вектора :
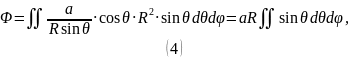
Сведём двойной интеграл к повторным, подставив пределы интегрирования:
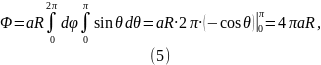
Вернёмся к теореме Остроградского-Гаусса:
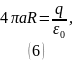
Отсюда можем найти заряд, помещённый внутри сферы:
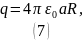
Ответ:
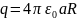 .
.
2.31. Шар
радиуса R имеет положительный
заряд. Объёмная плотность которого
зависит только от расстояния
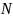 до его центра, как
до его центра, как
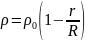 , где
, где
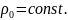 Пренебрегая влиянием вещества шара
найти:
Пренебрегая влиянием вещества шара
найти:
а) Модуль напряжённости электрического поля внутри и вне шара как функцию r
б) Максимальное
значение модуля напряжённости
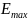 и соответствующее ему значение
и соответствующее ему значение
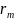 .
.
Решение. а) Будем считать, что сфера заряжена положительным зарядом
(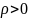 ).
По определению объёмной плотности
заряда:
).
По определению объёмной плотности
заряда:
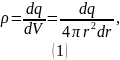
Для нахождения напряжённости электрического поля воспользуемся теоремой Гаусса:
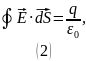
Рассмотрим 2 случая:
1)
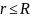 .
.
Найдём поток вектора сквозь поверхность шара.


Теперь найдём заряд, помещённый внутри шара.
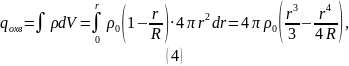
Согласно (2):
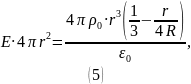
Таким образом, получили следующее выражение для напряжённости:
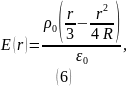
2)
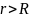 .
.
При поток будет оставаться таким же, так как направлен так же. Изменится лишь охваченный заряд и пределы интегрирования.
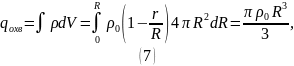
Согласно теореме Гаусса:
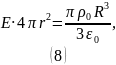
Итого для напряжённости электрического поля имеем:
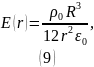
б) Найдём
точку максимума функции
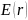 .
.
Для этого найдём от неё производную (при ) и приравняем её к нулю.
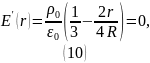
Решая уравнение (10) относительно , находим:
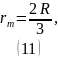
Подставляя полученный результат в (6), находим максимальное значение напряжённости электрического поля:
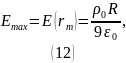
Ответ: a)
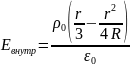 ;
;
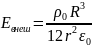 .
б)
.
б)
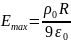 ;
;
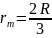 .
.
2.32. Система
состоит из шара радиуса
,
заряженного сферически-симметрично, и
окружающей среды, заполненной зарядом
с объемной плотностью
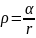 ;
;
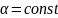 ;
– расстояние от центра шара. Пренебрегая
влиянием вещества, найти заряд шара,
при котором модуль напряженности
электрического поля вне шара не зависит
от
.
Чему равна эта напряженность?
;
– расстояние от центра шара. Пренебрегая
влиянием вещества, найти заряд шара,
при котором модуль напряженности
электрического поля вне шара не зависит
от
.
Чему равна эта напряженность?
Р ешение.
Для определённости предположим, что
.
ешение.
Для определённости предположим, что
.
Для нахождения напряжённости электрического поля используем теорему Гаусса.
Пусть
– заряд шара,
 – заряд, содержащийся в бесконечно
малом объёме
окружающей его среды.
– заряд, содержащийся в бесконечно
малом объёме
окружающей его среды.
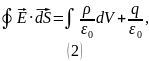
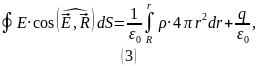
После вычисления интегралов получаем:
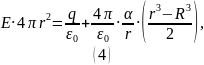
Упростим полученное выражение:
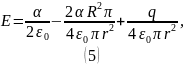
Как видно из
(5), при
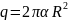 не зависит от
.
В таком случае модуль напряжённости
электрического поля будет равен:
не зависит от
.
В таком случае модуль напряжённости
электрического поля будет равен:
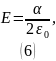
Ответ:
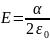 при
.
при
.
2.33. Внутри
шара, заряженного равномерно с объёмной
плотностью
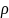 ,
имеется сферическая полость. Центр
полости смещён относительно центра
шара на расстояние
.
Пренебрегая влиянием вещества шара,
найти напряжённость
поля внутри полости.
,
имеется сферическая полость. Центр
полости смещён относительно центра
шара на расстояние
.
Пренебрегая влиянием вещества шара,
найти напряжённость
поля внутри полости.
Решение. Найдём напряжённость электрического поля в произвольной точке A внутри полости.
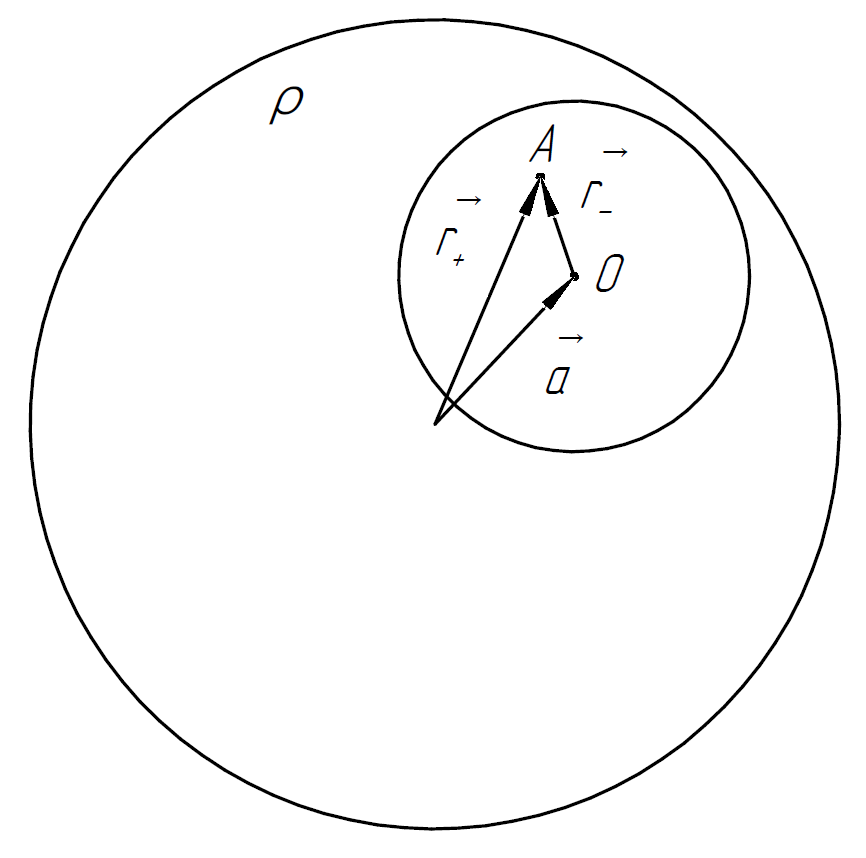 1)
Рассмотрим сплошной равномерно заряженный
шар с
.
1)
Рассмотрим сплошной равномерно заряженный
шар с
.
Используем для данного шара теорему Гаусса:
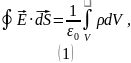
В качестве
замкнутой поверхности выберем сферическую
поверхность радиуса
 .
Вектора напряжённости, создаваемые
шаром, направлены вдоль радиусов от
центра шара. Тогда на такой сферической
поверхности модуль напряжённости
одинаков,
.
Вектора напряжённости, создаваемые
шаром, направлены вдоль радиусов от
центра шара. Тогда на такой сферической
поверхности модуль напряжённости
одинаков,
 .
.
Вернёмся к теореме Гаусса:
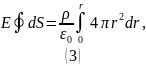
После вычисления интегралов имеем:
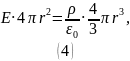
Получили напряжённость электрического поля, создаваемую равномерно заряженным шаром радиуса :
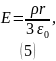
2) Согласно условию задачи, полость внутри шара не заряжена.
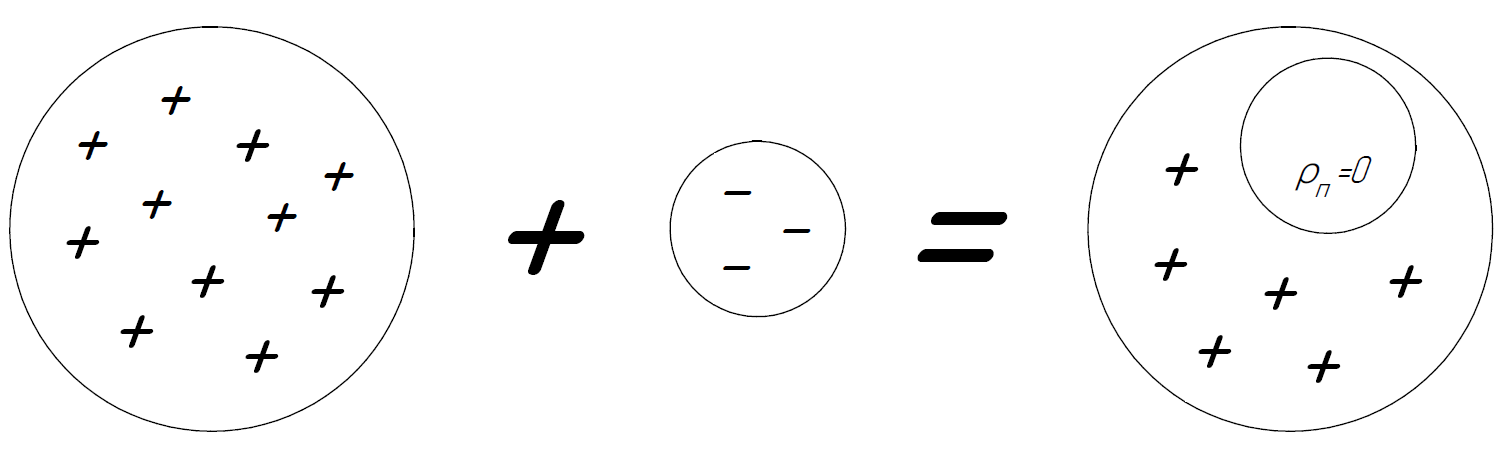 Будем
рассматривать электрическое поле в
данной области как результат суперпозиции
полей двух равномерно заряженных шаров:
Будем
рассматривать электрическое поле в
данной области как результат суперпозиции
полей двух равномерно заряженных шаров:
Согласно принципу суперпозиции для вектора напряжённости электрического поля, результирующий вектор в полости равен векторной сумме векторов напряжённости, создаваемых каждым из шаров:
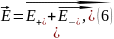
Тогда в произвольной точке A внутри полости:
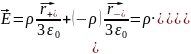
Ответ:
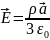 .
.
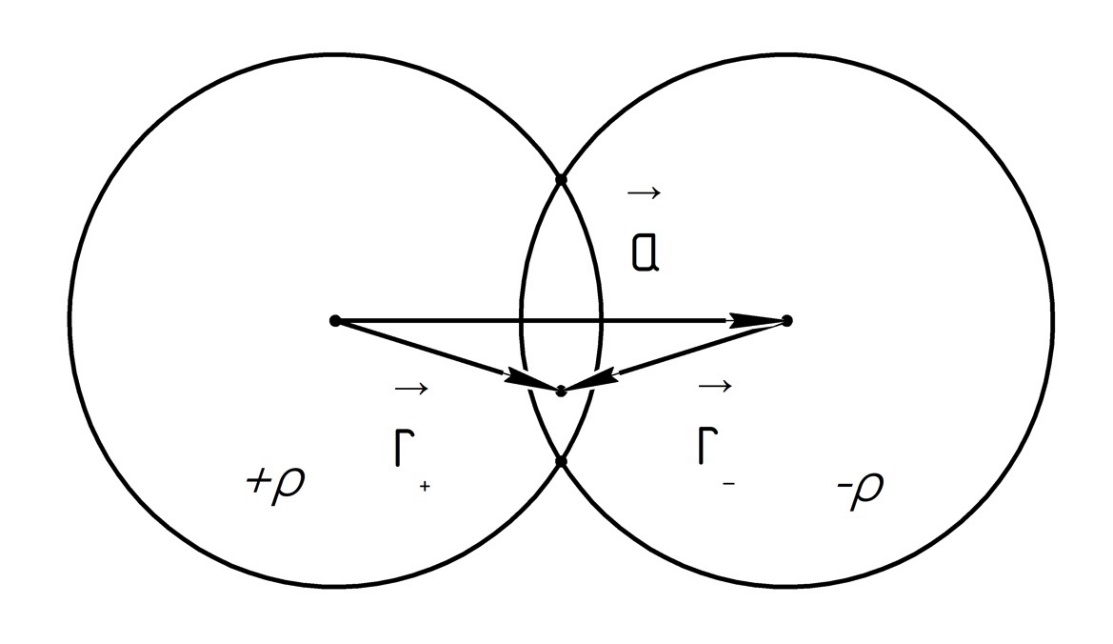 2.34.
Найти напряжённость
электрического поля в области пересечения
двух шаров, равномерно заполненных
разноимёнными по знаку зарядами с
объёмной плотностью
2.34.
Найти напряжённость
электрического поля в области пересечения
двух шаров, равномерно заполненных
разноимёнными по знаку зарядами с
объёмной плотностью
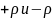 ,
если расстояние между центрами шаров
равно
.
,
если расстояние между центрами шаров
равно
.
Решение.
Объёмную плотность заряда в области пересечения шаров будем считать равной 0. Тогда напряжённость электрического поля будет равна векторной сумме векторов напряжённостей полей, создаваемых зарядами, расположенными вне полости:
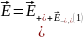
Найдём
напряжённость электрического поля,
создаваемую равномерно заряженным
шаром на расстоянии
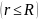 .
Согласно теореме Гаусса в интегральном
виде для вектора напряжённости
электрического поля:
.
Согласно теореме Гаусса в интегральном
виде для вектора напряжённости
электрического поля:
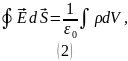
Перепишем скалярное произведение:
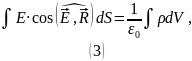
Напряжённость электрического поля равномерно заряженного шара направлена по радиусу, следовательно:
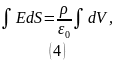
Вычисляя интегралы, находим зависимость напряжённости от расстояния от центра шара:
Для нахождения напряжённости электрического поля в области пересечения сложим напряжённости от двух шаров:
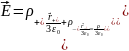
Ответ:
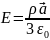
2.36. Имеются
два тонких проволочных кольца радиуса
каждое, оси которых совпадают. Заряды
колец равны
и
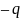 .
Найти разность потенциалов между
центрами колец, отстающими друг от друга
на расстояние
,
если
.
Найти разность потенциалов между
центрами колец, отстающими друг от друга
на расстояние
,
если
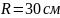 ,
,
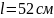 и
и
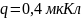 .
.
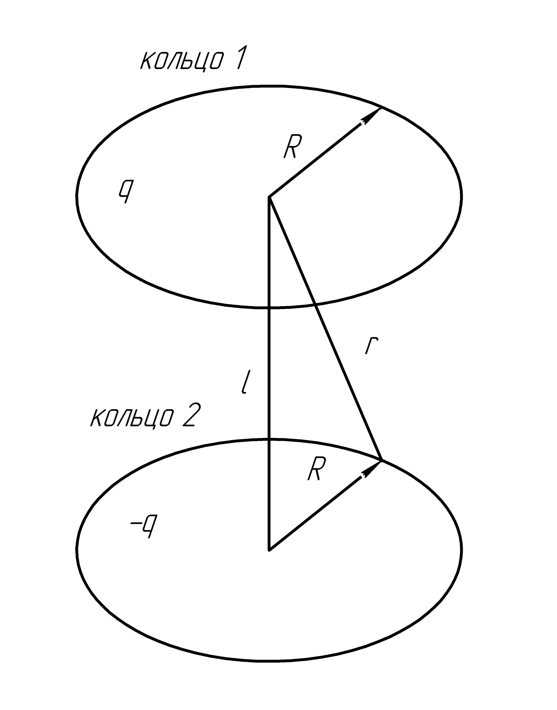 Решение.
Решение.
Разность потенциалов между центрами колец:
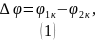
Рассмотрим кольцо 1:
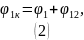
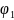 -
потенциал в центре первого кольца от
заряда кольца 1,
-
потенциал в центре первого кольца от
заряда кольца 1,
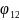 -
потенциал в центре первого кольца от
заряда кольца 2.
-
потенциал в центре первого кольца от
заряда кольца 2.
Вычислим потенциал в центре первого кольца, пользуясь определением потенциала:
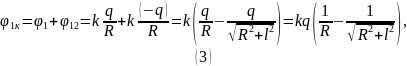
Теперь рассмотрим кольцо 2:
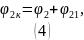
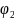 -
потенциал в центре второго кольца от
заряда кольца 2,
-
потенциал в центре второго кольца от
заряда кольца 2,
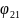 -
потенциал в центре второго кольца от
заряда кольца 2.
-
потенциал в центре второго кольца от
заряда кольца 2.
Аналогично (3) вычисляем потенциал в центре второго кольца:
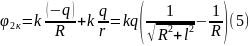
Можем найти
требуемую разность потенциалов между
центрами колец: (4

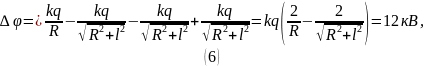
Ответ:
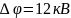 .
.
2.37 Бесконечно
длинная прямая нить заряжена равномерно
с линейной плотностью
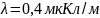 .
Вычислить разность потенциалов точек
1 и 2, если точка 2 находится дальше от
нити, чем точка 1, в
.
Вычислить разность потенциалов точек
1 и 2, если точка 2 находится дальше от
нити, чем точка 1, в
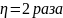 .
.
Решение.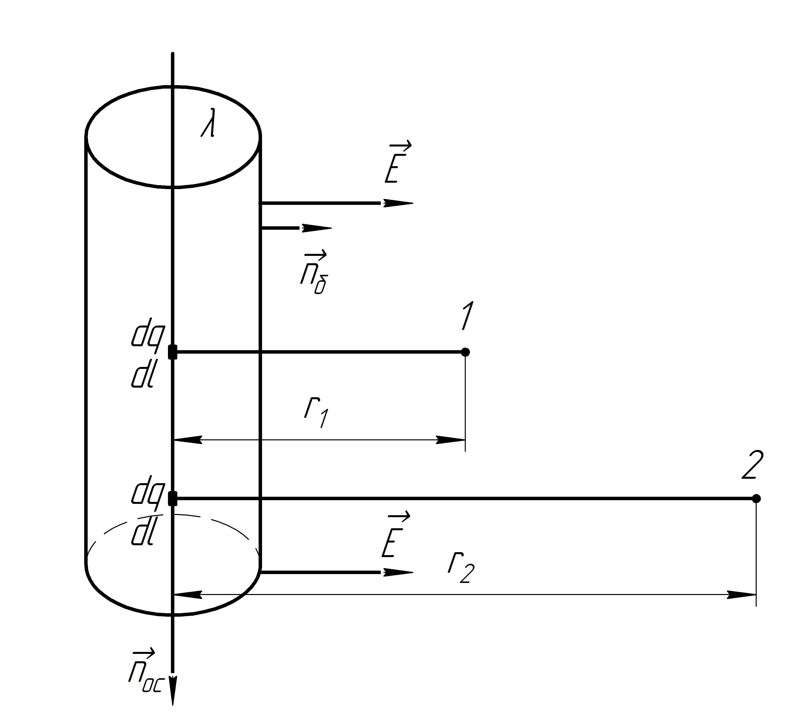
Нам необходимо найти напряженность электрического поля заряженной нити для вычисления разности потенциалов с помощью связи напряжённости и потенциала:
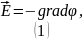 Для
нахождения
«дорисуем» вокруг нити цилиндр (гауссову
поверхность) и выразим поток напряженности
электрического поля через него с помощью
теоремы Гаусса:
Для
нахождения
«дорисуем» вокруг нити цилиндр (гауссову
поверхность) и выразим поток напряженности
электрического поля через него с помощью
теоремы Гаусса:
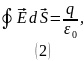
Поток через цилиндр вычислим следующим образом:
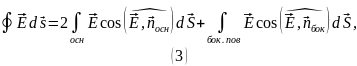
Так как угол
между вектором напряженности и нормалью
к основанию цилиндра равен
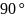 ,
то
,
то
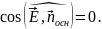 Таким образом, поток через основания
цилиндра равен нулю.
Таким образом, поток через основания
цилиндра равен нулю.
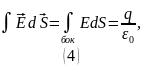
После вычисления интеграла и использования определения линейной плотности заряда получаем:
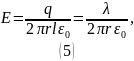
Так как модуль напряжённости электрического поля зависит только от расстояния от нити , то можем переписать (1) для модуля :
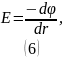
Вычислим разность потенциалов по формуле по формуле (6), подставив :
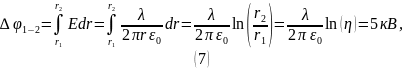
Ответ:
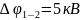
2.38. Тонкое
кольцо радиуса
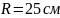 имеет заряд
имеет заряд
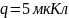 неравномерно
распределённый по кольцу. Найти работу
электрических сил при перемещении
точечного заряда
неравномерно
распределённый по кольцу. Найти работу
электрических сил при перемещении
точечного заряда
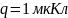 из центра кольца по произвольному пути
в точку, находившуюся на оси кольца на
расстоянии
из центра кольца по произвольному пути
в точку, находившуюся на оси кольца на
расстоянии
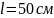 от его центра.
от его центра.
 Решение.
Работу по перемещению точечного
заряда
можем найти с помощью выражения:
Решение.
Работу по перемещению точечного
заряда
можем найти с помощью выражения:
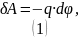
Потенциал, создаваемый заряженным кольцом, в его центре по определению:
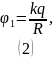
Аналогично потенциал на расстоянии от центра кольца:
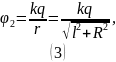
Из (1) следует, что в нашем случае работу по перемещению электрического заряда из точки 1 в точку 2 можем найти как:
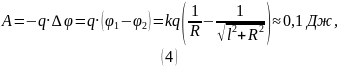
Ответ:
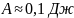 .
.
2.43. Найти
напряжённость электрического поля,
потенциал которого имеет вид
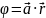 ,
где
– постоянный вектор,
– радиус-вектор точки поля.
,
где
– постоянный вектор,
– радиус-вектор точки поля.
Решение. Связь напряжённости электрического поля и потенциала:
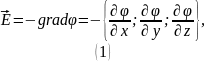
Найдём потенциал:
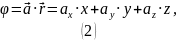
Теперь можем найти :
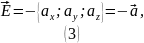
Ответ:
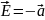 .
.
2.50. Система
состоит из заряда
,
равномерно распределённого по
полуокружности радиуса
,
в центре которой находится точечный
заряд
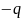 .
Найти: электрический дипольный момент
этой системы;
.
Найти: электрический дипольный момент
этой системы;
Решение. Разделим кольцо на бесконечно малые части длины . Так как заряд распределён по кольцу равномерно, то каждая такая часть имеет заряд .
Электрический
диполь состоит из двух разноимённых
одинаковых по модулю зарядов, следовательно
для нахождения дипольного момента
мысленно разобьём заряд
на бесконечно малые части
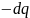 .
.
Дипольный электрический момент для системы зарядов и , находящихся на расстоянии друг от друга:
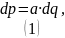
Можем воспользоваться линейной плотностью заряда:
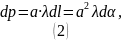
Выберем на кольце 2 симметрично расположенных отрезка . Заряды, находящиеся на этих отрезках, можно считать точечными.
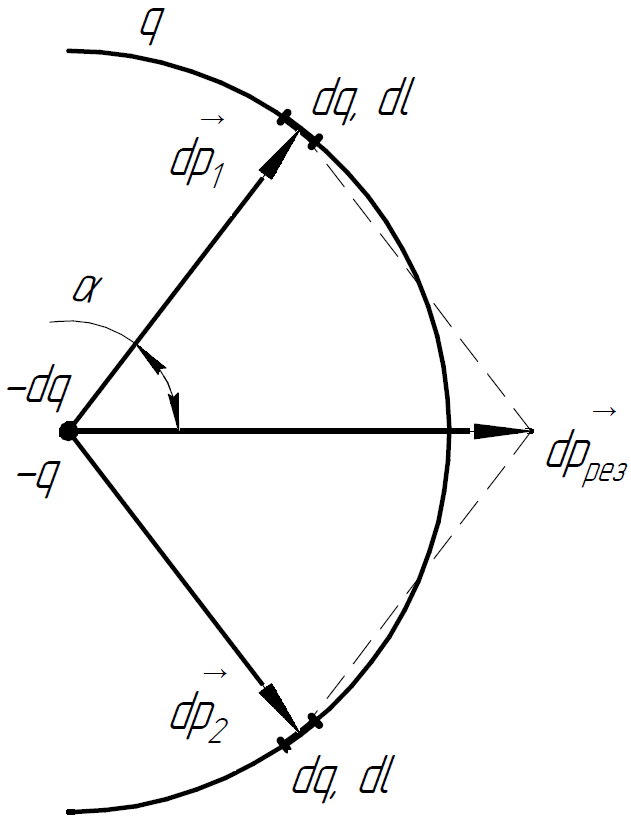 Проведём
вектора дипольного момента. Результирующий
вектор направлен горизонтально, поэтому
для вычисления
Проведём
вектора дипольного момента. Результирующий
вектор направлен горизонтально, поэтому
для вычисления
 достаточно просуммировать только
горизонтальные составляющие
достаточно просуммировать только
горизонтальные составляющие
 .
.
Окончательно получаем:
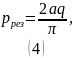
Ответ:
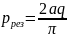 .
.
2.52. Какую
работу против сил электрического поля
надо совершить, чтобы перенести диполь
с электрическим моментом
из положения 1, где напряжённость поля
равна
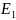 ,
в положение 2 с напряжённостью
,
в положение 2 с напряжённостью
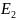 ?
?
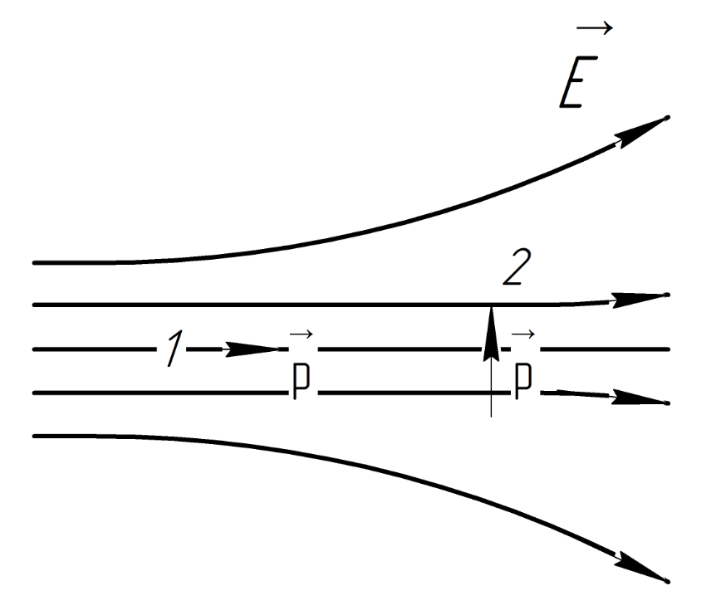 Решение:
Работа, совершаемая против сил
потенциального поля:
Решение:
Работа, совершаемая против сил
потенциального поля:
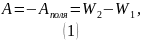
Потенциальная энергия диполя в электростатическом поле с напряжённостью :
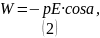
Для положения 1:
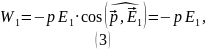
Для положения 2:
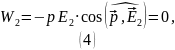
Возвращаясь к (1), находим искомую работу:
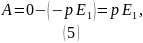
Ответ:
2.53. Диполь
с электрическим моментом
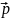 находится на расстоянии
от длинной прямой нити, заряженной
равномерно с линейной плотностью
.
Найти силу
находится на расстоянии
от длинной прямой нити, заряженной
равномерно с линейной плотностью
.
Найти силу
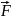 ,
действующую на диполь, если вектор
ориентирован:
,
действующую на диполь, если вектор
ориентирован:
a) вдоль нити;
б) по радиусу вектору .
Решение. Для определённости будем считать, что .
a) Нарисуем цилиндр, охватывающий нить и имеющий на своей границе диполь. В условии задачи ничего не сказано насчёт ориентации диполя. Предположим, что вектор направлен вверх.
Сила, действующая на диполь, помещённый в неоднородное электрическое поле:
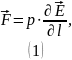
Проекция этой силы на ось , проходящую через диполь:
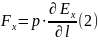
Такое
расположение осей обусловлено тем, что
нам будет удобнее искать проекцию
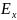 ,
если E лежит на оси
.
В таком случае вектор напряжённости
электрического поля представим в виде:
,
если E лежит на оси
.
В таком случае вектор напряжённости
электрического поля представим в виде:
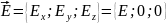
Отсюда делаем
вывод, что
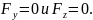
Согласно теореме Гаусса для вектора :
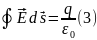
В качестве гауссовой поверхности используем цилиндр:
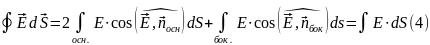
Так как угол между вектором напряжённости и нормалью к основанию цилиндра равен , то:
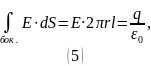
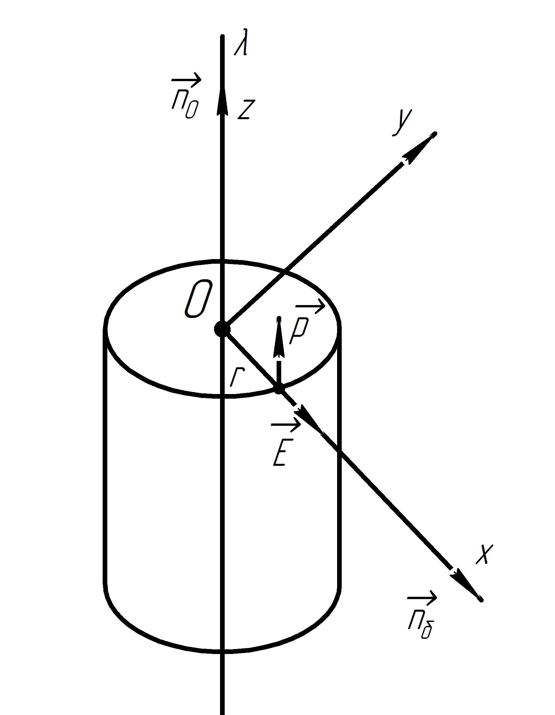 Воспользуемся
определением линейной плотности заряда:
Воспользуемся
определением линейной плотности заряда:
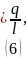
Тогда (5) примет вид:
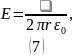
Вернёмся к
рисунку, согласно которому
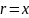 .
Тогда проекция вектора
на ось
:
.
Тогда проекция вектора
на ось
:
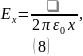
Теперь
вычислим силу с помощью (2) (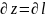 ,
так как производную берём по направлению
):
,
так как производную берём по направлению
):
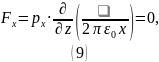
Так как
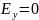 ,
,
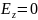 ,
то
,
то
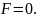
Ответ:
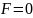 .
.
б) Вновь направим вектор напряжённости электрического поля вдоль оси .
Так как в данном случае диполь также ориентирован вдоль оси , то:
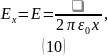
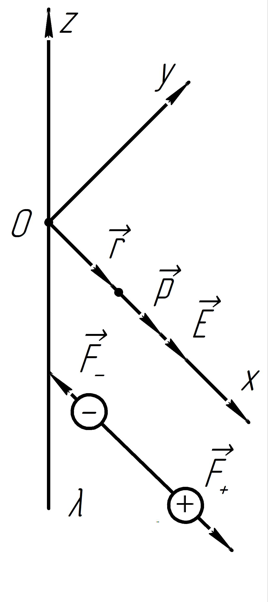 Из
решения прошлого пп. следует, что
Из
решения прошлого пп. следует, что
 .
Тогда сила, действующая на диполь (
.
Тогда сила, действующая на диполь ( :
:
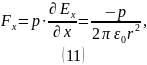
Знак «минус» говорит о том, что сила направлена противоположно оси – к нити.
Ответ:
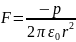 .
.
2.57. Между
двумя большими параллельными пластинами,
отстоящими друг от друга на расстояние
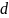 ,
находится равномерно распределенный
объемный заряд. Разность потенциалов
пластин равна
,
находится равномерно распределенный
объемный заряд. Разность потенциалов
пластин равна
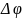 .
При каком значении объемной плотности
заряда напряженность поля вблизи одной
из пластин будет равна нулю? Какова
будет при этом напряженность поля у
другой пластины?
.
При каком значении объемной плотности
заряда напряженность поля вблизи одной
из пластин будет равна нулю? Какова
будет при этом напряженность поля у
другой пластины?
Решение. Рассмотрим напряжённость электрического поля, создаваемую заряженной пластиной.
Используем теорему Гаусса для нахождения напряженности электрического поля. В качестве гауссовой поверхности возьмём цилиндр.
Поверхностная плотность заряда по определению:
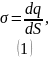
Теорема Гаусса для вектора :
Вычисляем поток через цилиндр:
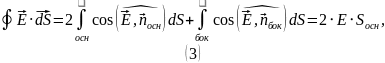
 Подставляя
полученный результат в (2), находим:
Подставляя
полученный результат в (2), находим:
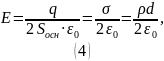
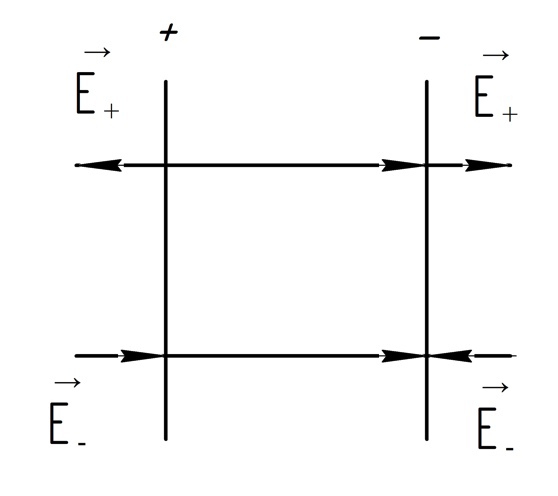 Для
двух разноименно заряженных пластин:
Для
двух разноименно заряженных пластин:
В области между пластинами поля складываются (т. к. имеют одинаковые направление):
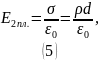
Вне пластин складываемые поля имеют разное напряжение направление, результирующая напряженность равна 0.
2) Вычислим поле распределённого по объёму заряда.
Для вычисления
напряженности поля объёмного заряда
используем теорему Гаусса. В качестве
замкнутой поверхности возьмём
параллелепипед с площадью основания
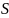 и шириной
и шириной
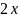 .
На правом и левом основаниях напряженность
постоянна по модулю и направлению.
.
На правом и левом основаниях напряженность
постоянна по модулю и направлению.
Тогда теорема Гаусса (2) запишется в виде:
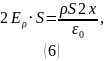
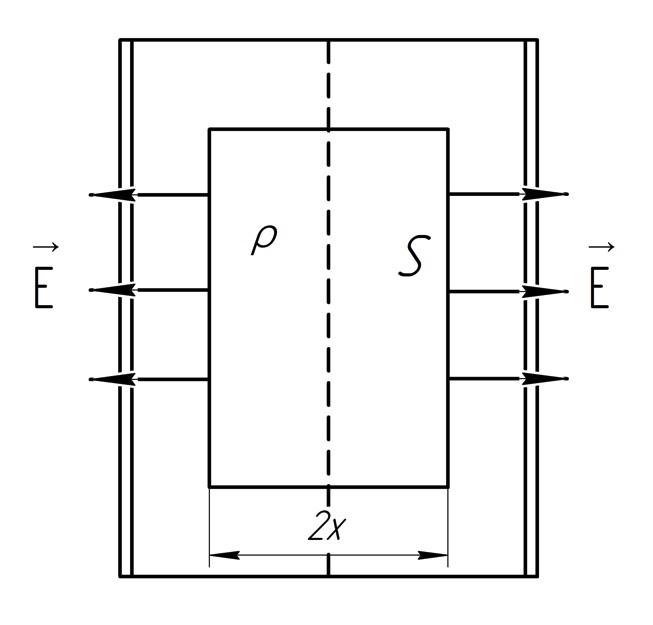 Так
как
Так
как
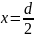 , то напряжённость электрического поля
вблизи пластин равна:
, то напряжённость электрического поля
вблизи пластин равна:
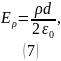
Ответ:
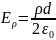 .
.
2.58. Потенциал
поля внутри заряженного шара зависит
от расстояния до его центра как
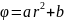 ,
где
и
,
где
и
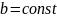 .
Найти распределение объемного заряда
.
Найти распределение объемного заряда
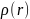 внутри шара.
внутри шара.
Решение. Запишем выражения для расстояния от центра шара в декартовой системе координат:
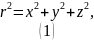
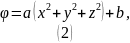
Используем уравнение Пуассона:
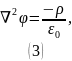
Лапласиан потенциала:
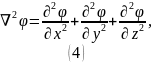
После вычисления производных получаем:
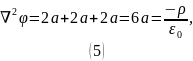
Таким образом, объёмная плотность заряда шара:
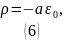
Ответ:
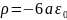 .
.
