ЛР2

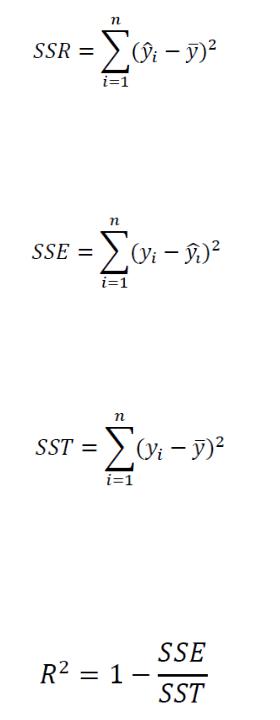
. (4)

Величина SSE называется суммой квадратов ошибки. Она показывает степень варьирования целевого значения вокруг линии регрессии. Формула расчета следующая:

. (5)

Величина SST называется общей суммой квадратов. Она дает информа-

цию о том, насколько далеко распределенные значения находятся от простого среднего выборочного. Формула расчета следующая:

. (6)

Коэффициент детерминации 2 отражает качество модели и определя-

ется через остаточную сумму квадратов и общую дисперсию , таким обра-

зом выражая, какая доля дисперсии целевой переменной может быть объяс-

нена предиктором. Формула расчёта:

. (7)

Для получения качественных оценок параметров уравнения регрессии необходимо следить за выполнимостью предпосылок МНК. Применяя МНК мы предполагаем, что остатки εi подчиняются условиям Гаусса-Маркова, дан-

ное предположение необходимо проверить, после построения уравнения ре-

грессии.

4

равенстве нулю коэффициента корреляции, а следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетеро-

скедастичности принимается.

В тесте Гольдфельда-Квандта также предполагается, что стандартное от-

клонение пропорционально значению переменной Х в этом наблю-

дении, т.е. . Предполагается, что имеет нормальное рас-

пределение и отсутствует автокорреляция остатков.

Тест Гольдфельда-Квандта состоит в следующем:

1.Все наблюдений упорядочиваются по величине Х.

2.Вся упорядоченная выборка после этого разбивается на три под-

выборки размерностей соответственно.

3.Оцениваются отдельные регрессии для первой подвыборки (пер-

вых наблюдений) и для третьей подвыборки ( последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям Х верно, то дисперсия регрессии по первой подвыборке (сумма квадратов откло-

нений ) будет существенно меньше дисперсии регрессии по третьей

подвыборке (суммы квадратов отклонений ).

4.Для сравнения соответствующих дисперсий строится следующая -

ных дисперсий ( - количество объясняющих переменных в уравнении ре-

грессии).

При сделанных предположениях относительно случайных отклонений построенная статистика имеет распределение Фишера с числами степеней сво-

5.Если , то гипотеза об отсутствии гетеро-

скедастичности отклоняется (здесь α - выбранный уровень значимости).

Естественным является вопрос: какими должны быть размеры подвыбо-

рок для принятия обоснованных решений? Для парной регрессии Гольдфельд и Квандт предлагают следующие пропорции: .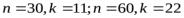

Этот же тест может быть использован при предположении об обратной пропорциональности между и значениями объясняющей переменной. При этом статистика Фишера примет вид: .

7

ПОЛНЫЙ КОД ПРОГРАММЫ

using CSV

using DataFrames using Statistics using Plots

var = 1

dfA = CSV.read("A_$var.csv", DataFrame) name = "A"

#dfA = CSV.read("B_$var.csv", DataFrame) #name = "B"

function ols_coeff(x::Vector, y::Vector) #вычисление коэффициентов регрессии mean_x = mean(x)

mean_y = mean(y) mean_x_square = mean(x.*x) mean_xy = mean(x.*y)

b1 = (mean_xy - mean_x*mean_y)/(mean_x_square - mean_x*mean_x) b0 = mean_y - b1*mean_x

return b0, b1

end

function parametres_of_model(x::Vector, y::Vector) #вычисление параметров модели SSR, SSE, SSTO, R_square = 0, 0, 0, 0

residuals, var = [], [] y_mean = mean(y)

(b0, b1) = ols_coeff(x, y) y_model = x.*b1.+b0

residuals = y.-y_model #остатки

var = residuals.*residuals #остатки в квадрате

SSR = sum((residuals.- y_mean).*(residuals.- y_mean)) #регрессия суммы квад-

ратов

SSE = sum(var) #суммарная ошибка регрессии

SSTO = sum((y.- y_mean).*(y.- y_mean)) #общая дисперсия

R_square = 1 - SSE/SSTO #коэффициент детерминации

return y_model, residuals, var, round(SSR,digits = 3), round(SSE, digits = 3), round(SSTO,digits = 3), round(R_square,digits = 3)

end

function Goldfeld_Quandt_test(data::DataFrame) #тест Голдфелда-Квандта data_sort = sort(data, :x)

k = 25 # число элементов в каждой выборке sample_1 = first(data_sort, k) #первая выборка sample_2 = last(data_sort, k) #вторая выборка

b0_1, b1_1 = ols_coeff(sample_1.x, sample_1.y) #расчет коэффициентов

8

b0_2, b1_2 = ols_coeff(sample_2.x, sample_2.y) y_model_1 = b0_1.+sample_1.x.*b1_1

y_model_2 = b0_2.+sample_2.x.*b1_2

er_1 = sample_1.y.-y_model_1 #ошибки первой выборки er_2 = sample_2.y.-y_model_2

SSE_1 = sum(er_1.^2) #суммарная ошибка регрессии для первой вбыорки

SSE_2 = sum(er_2.^2)

F = SSE_2/SSE_1#вычисление F

return (k, round(F, digits = 4))

end

function Spirmen_test(x::Vector, er::Vector) #вычислении коэфф. ранг. корр. Спир-

мена

er = abs.(er)

x_sort = sort(x) # сортировка er_sort = sort(er)

rang_x, rang_er = [], [] n = length(x)

for item in x #сопоставление элементу из начального вектора его индекса в сортированном,

#это и будет его ранг

# !!! предполагаем, что одинаковых значений в векторе нет rang = indexin(item, x_sort)

append!(rang_x, rang) # добавление индекса/ранга в соотвествующий вектор

end

for item in er

rang = indexin(item, er_sort) append!(rang_er, rang)

end

r_Spirmen = 1 - 6*(sum((rang_x.-rang_er).^2))/(n^3-n) #вычисление статистики t = r_Spirmen*sqrt(n-2)/sqrt(1-r_Spirmen^2) #вычисление её t-критерия

return t, r_Spirmen end

y_model, er, var, SSR, SSE, SSTO, R_square = parametres_of_model(dfA.x, dfA.y)

println(Spirmen_test(dfA.x, er)) println(Goldfeld_Quandt_test(dfA))

p1 = scatter(dfA.x, dfA.y, label = "исходные данные", xlabel = "x", ylabel = "y", title = "Выборка $name")

plot!(dfA.x, y_model, label = "модель", annotate = [

9

(-2.5, 1, text("SSR = $SSR", 7, :left)), (-2.5, 0.7, text("SSE = $SSE", 7, :left)), (-2.5, 0.4, text("SSTO = $SSTO", 7, :left)), (-2.5, 0.1, text("R^2 = $R_square", 7, :left)),

]

)

p2 = scatter(dfA.x, er, xlabel = "x", ylabel = "ошибка регрессии", title = "Ошибка регрессии $name", legend = false)

p3 = scatter(dfA.x, var, xlabel = "x", ylabel = "дисперсия регрессии", title = "Дисперсия регрессии $name", legend = false)

p4 = histogram(er, title = "Распределение остатков $name", legend = false) xlims!(minimum(er)*1.2, maximum(er)*1.2)

plot(p1) savefig("sample_$name.png")

plot(p2) savefig("er_$name.png")

plot(p3) savefig("var_$name.png")

plot(p4) savefig("hist_$name.png")

10