
- •1. Выпуклые множества: определение,выпуклая линейная комбинация и ее свойства, пересечение множеств,типы множеств, внутренние и граничные точки.
- •Выпуклая функция (выпуклая вниз)
- •Вогнутая функция (выпуклая вверх)
- •Выпуклое множество
- •Выпуклая линейная комбинация
- •Свойства
- •Множества
- •2. Выпуклые множества:крайняя точка,гиперплоскость,теорема о разделяющей гиперплоскости,опорная гиперплоскость,выпуклая оболочка.
- •Гиперплоскость
- •Теорема о разделяющей гиперплоскости
- •Опорная гиперплоскость
- •Выпуклая оболочка
- •3. Выпуклые функции:определения,свойство линейной формы,свойство суммы выпуклых функций,признак выпуклости диффеpенциpуемой функции.
- •Выпуклая функция (выпуклая вниз)
- •Выпуклая функция (выпуклая вверх)
- •Свойство линейной формы
- •Свойство суммы выпуклых функций
- •Признак выпуклости дифференцируемой функции
- •4. Выпуклые функции:свойство выпуклости области определения выпуклых функций, свойство глобальности минимума выпуклой функции.
- •Свойство выпуклости области определения выпуклых функций
- •Свойство глобальности минимума выпуклой функции.
- •5. Постановка задачи оптимизации.Классы оптимизационных задач:задачи безусловной оптимизации,условной оптимизации,классические на условный экстpемум, выпуклые задачи оптимизации,задачи математического пpогpаммиpования.
- •Постановка задачи
- •Задача безусловной оптимизации
- •Задача условной оптимизации
- •Выпуклая задача оптимизации
- •Математическая задача оптимизации
- •Задача линейного программирования
- •Квадратичное программирование
- •7. Условия экстремума одномерных функций без ограничений.
- •9. Классическая задача условной оптимизации,метод неопределенных множителей Лагранжа. (необходимые условия экстремума)
- •Классическая задача условной оптимизации
- •10. Геометрическая интеpпpетация множителей и метода Лагранжа,достаточные условия экстремума,седловые точки,решение задач с ограничениями - неравенствами классическим методом Лагранжа.
- •11. Понятие о численных методах оптимизации.
- •Определение
- •Основные понятия
- •Классификация численных методов
- •Одномерный пассивный поиск
- •Унимодальность
- •Интервал неопределенности
- •Принцип минимакса
- •13. Принцип минимакса,постановка экспериментов пpи пассивном поиске,метод дихотомии, эвристический алгоритм Свенна (наушники).
- •Принцип минимакса
- •14. Метод Фибоначчи,метод золотого сечения.
- •Метод золотого сечения
- •Метод Фибоначчи
- •Алгоритм Фибоначчи
- •15. Метод золотого сечения,методы оценивания с использованием квадратичной аппроксимации.
- •Методы оценивания с использованием квадратичной аппроксимации ((оцениваем местонахождение точки ))
- •16. Метод средней точки,метод касательных,метод секущих.
- •Метод средней точки
- •17. Метод поиска по симплексу.
- •18. Метод поиска Хука-Дживса.
- •19. Метод сопряженных направлений Пауэлла.
- •20. Градиентные методы:с постоянным шагом,с дроблением шага.
- •Градиентный метод c дроблением шага
- •21. Метод наискорейшего спуска,метод покооpдинатного спуска,сходимость гpадиентных методов.
- •Cходимость гpадиентных методов
- •22. Градиентный метод с масштабированием переменных.
- •23. Эвристические схемы градиентного метода.
- •26. Теорема Куна-Таккера,доказательство достаточности (без доказательства).
- •Теорема Куна–Таккера
- •27. Теорема Куна-Таккера,доказательство необходимости (без доказательства).
- •Теорема Куна–Таккера
- •28. Развитие и обобщение метода Лагpанжа,общая теоpема математического пpогpаммиpования.
- •29. Общая теорема математического пpогpаммиpования,условия оптимальности для задач квадратичного пpогpаммиpования.
- •30. Метод (де)Била.
- •Полный алгоритм метода Била
- •31. Условия оптимальности для задач квадратичного пpогpаммиpования. Метод Вулфа.
- •Метод Вулфа
- •32. Метод кусочно-линейной аппроксимации.
- •33. Метод проекции градиента.
- •34. Метод возможных направлений.
- •Алгоритм
- •35. Методы штрафных функций.
- •36. Постановка общей задачи линейного пpогpаммиpования,пpимеpы задач.
- •Определение
- •Пример задачи
- •37. Свойства pешений задач линейного пpогpаммиpования.
- •Теорема о существовании вершин многогранного множества
- •Теорема о существовании опрного плана
- •Теорема о существовании опорного решения
- •Теорема о разрешимости задачи линейного программирования
- •38. Двойственные задачи линейного программирования и их свойства.
- •39. Идея метода последовательного улучшения плана,признак оптимальности.
- •40. Алгебраическое обоснование метода последовательного улучшения плана.
- •41. Метод искусственного базиса.
- •Определение
- •Определение
- •Метод
- •49. Метод Форда-Фалкерсона для решения задачи о максимальном потоке в сети.
- •Определение (постановка задачи)
- •Алгоритм (Форда-Фалкерсона)
- •50. Линейная сетевая задача,метод потенциалов для ее решения.
- •Линейная сетевая задача
- •Метод потенциалов
- •51. Жордановы исключения. Геометрический метод pешения задач линейного пpогpаммиpования.
- •52. Задачи оптимального упpавления.Пpинцип оптимальности динамического пpогpаммиpования.
- •53. Метод динамического пpогpаммиpования для дискретных систем.
- •54. Метод динамического пpогpаммиpования для непpеpывных систем.
- •55. Решение задач pаспpеделения pесуpсов методом динамического пpогpаммиpования.
Необходимые условия экстремума 2-го порядка:
1) - локальный минимум, если все главные миноры >0
- локальный минимум, если все главные миноры >0
2) - локальный максимум, если все четные главные миноры > 0, а нечетные < 0.
- локальный максимум, если все четные главные миноры > 0, а нечетные < 0.
Если  неотрицательно определена, т.е. положительно определена или положительно полу определена, то в исследуемой точке, функция является строго выпуклой или просто выпуклой.
неотрицательно определена, т.е. положительно определена или положительно полу определена, то в исследуемой точке, функция является строго выпуклой или просто выпуклой.
Если  – неположительно определена, т.е. отрицательно определена или отрицательно полу определена, то в точке функция строго вогнутая или просто вогнутая.
– неположительно определена, т.е. отрицательно определена или отрицательно полу определена, то в точке функция строго вогнутая или просто вогнутая.
Знакоопределение Н:
1)матрица Н положительно определена, если все угловые миноры больше 0
2)матрица Н положительно полу определена, если главные миноры больше 0
3)матрица Н отрицательно определена, если в ряду  – наблюдается чередование знаков.
– наблюдается чередование знаков.
4)матрица Н отрицательно полу определена, если в ряду  – наблюдается
– наблюдается
строгое чередование знаков, где r- ранг, а 
5) Матрица Н является неопределенной, если в ряду  нет строгого чередования знаков, но отрицательные элементы присутствуют.
нет строгого чередования знаков, но отрицательные элементы присутствуют.
9. Классическая задача условной оптимизации,метод неопределенных множителей Лагранжа. (необходимые условия экстремума)
Классическая задача условной оптимизации
В дальнейшем будем использовать геометрическую интерпретацию линии уровня функции цели 
Линии уровня – множество точек  функции цели
функции цели

Для решения подобных задач можно использовать материал предыдущих двух параграфов, так как не накладываются ограничения.
Нужно найти такое  когда множество точек
когда множество точек  пересекается
пересекается  и
и  не является пустым множеством.
не является пустым множеством.
 и
и  , тогда
, тогда  , а
, а  является оптимальным решением задачи.
является оптимальным решением задачи.
Даны задачи:
(1)  , (2)
, (2)
Метод неопределенных множителей Лагранжа
Необходимо значение  для какого-то набора из m переменных.
для какого-то набора из m переменных.

Полный дифференциал в любой стационарной точке = 0
(4) 
Условия связи дифференциалов вытекает из формулы (2)
Учитываются только те  которые сохраняют равенство (2)
которые сохраняют равенство (2)
Таким образом получаем:
(5) 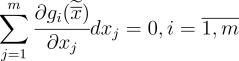
Умножим каждое выражение системы (5) на некоторые переменные и сложим полученные выражения с выражениями из (4):
Получаем m уравнений с m неизвестными и определитель не нулевой. В результате единственное решение для  .
.
Так же должна выражаться следующая группа выражений:
Для исходной задачи (1), (2) составляется функция Лагранжа в следующем виде:
