Функция цели имеет вид: 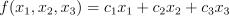. Данную функцию нужно максимизировать, то есть найти наибольшую прибыль.

Возникают ограничения для каждого ресурса:

Также появляются ограничения на

Дальше все решается симплекс методом с первых практик.

Квадратичное программирование

Это особый тип задачи, в котором функция цели квадратична, а условия линейны

7. Условия экстремума одномерных функций без ограничений.

1.​ Необходимое условие экстремума

Необходимым условием является теорема Ферма:

Пусть функция f(x) дифференцируема в некотором промежутке (.) х и во внутренней точке этого промежутка принимает наибольшее(наименьшее) значение тогда, когда

. Таким образом, экстремумы дифференцируемой функции следует искать в

стационарных точках, то есть в тех точках, в которых производная равняется нулю.

Правила нахождения глобального экстремума:

1)Находим множество стационарных точек.

2)Находим множество точек разрыва функции

3)Находим множество точек разрыва производной

4)Находим множество граничных точек

5)После этого необходимо вычислить значения функции в этих точках и выбрать среди них наибольшее и наименьшее значения.

2.​ Достаточные условия экстремума

Достаточным условием нахождения экстремума является теорема Вейерштрасса: Любая непрерывная Функция f(x) заданная на замкнутом ограниченном множестве достигает своего минимума во внутренней или граничной точке множества

Бывает, что 2-я производная = 0, тогда используют аппарат старших производных:

Допустим, что в (.) существует производных функции , причем все производные порядка от до равны нулю, а производная порядка не равна нулю. Тогда если

-четное и производная в точке больше 0, то в точке находится локальный минимум функции.

Если – нечетная, то ничего сказать нельзя.

знакоопределенности квадратичной формы.

Необходимое условие локального экстремума:

Пусть функция определена, непрерывна и непрерывно дифференцируема в

некоторой окрестности (.) . Тогда, для того чтобы в (.) достигался экстремум, необходимо

выполнить условия .

, где - стационарная точка.

Матрица Гессе - матрица частных производных второго порядка, вычисленных в данной

точке.

Достаточные условия экстремума:

1)Для того, чтобы матрица Гессе была положительно определена и точка являлась точкой локального минимума, необходимо и достаточно, чтобы знаки угловых миноров были >0.

2)Для того, чтобы матрица Гессе была отрицательно определена и точка

являлась точкой локального максимума, необходимо и достаточно, чтобы знаки угловых

миноров чередовались, начиная с отрицательного.