Первый шаг завершен, необходимо записать размер “хода” для рассмотренного пути. В нашем случае ABEF=2.

Продолжать алгоритм необходимо до тех пор, пока не останется ни единого пути из А в F. В конце необходимо посчитать сумму путей, что и будет являться ответом.

50. Линейная сетевая задача,метод потенциалов для ее решения.

Линейная сетевая задача

Это такая задача об оптимальном потоке вида:

При 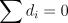, что является необходимым условием баланса для сети, мы имеем сбалансированную задачу, в которой соответствует пунктам производства, а

пунктам потребления, – промежуточным пунктам, где груз не производится и не

потребляется. Пропускные способности – не ограничены.

Метод потенциалов

Рассмотрим алгоритм метода потенциалов на примере:

На данном неор графе вершины 4,5 – пункты производства, вершины 2,3 – пункты потребления. Рядом с каждой вершиной записана величина ее запаса (потребности). Каждому

ребру соответствует свое значение удельной стоимости (в любую сторону одинаковый).

Сам по себе алгоритм устроен так: на первом этапе специальным методом строится допустимое базисное решение сбалансированной транспортной задачи. На втором этапе с помощью метода потенциалов это допустимое базисное решение оптимизируется.

Предварительный этап:

Для построения базисного плана используется следующий алгоритм:

●​ На данном этапе строится система базисных дуг. На данном шаге каждая дуга будет отмечаться линией с двумя стрелками, направленные в обе стороны. Процесс построения сопровождается расстановкой и корректировкой пометок у вершин. ​ В начале всем вершшинам присваивают нулевые пометки. В качестве базисной дуги выбирают

любое ребро; выберем ребро 1-5 и пометим его стрелками. Одновременно с этим увеличим на единицу пометки у вершин, связанных этой базисной дугой. Затем поочередно связываем базисными дугами вершины, имеющие нулевые пометки, и вершины с пометками, отличных от нуля. При проведении очередной базисной дуги пометки вершин, которые она соединяет, должны быть увеличены на единицу. Построение закончено, когда все вершины сети будут почемены ненулевыми оценками. На рисунке ниже построение проводилось в следующем порядке: 1-5; 5-3; 5-4; 3-2

●​ Следующий этап построения базисного плана. Данный этап предназначен для определения величины потока по каждой базисной дуге и однозначной ориентации базисных дуг. Построение осуществляется в поредке как на рисунке:

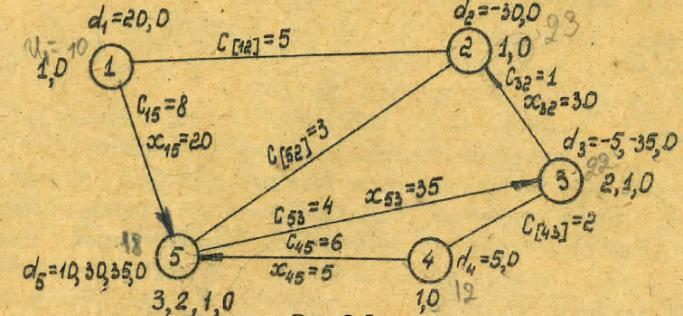
Выбирается любая вершина с пометкой – единица. Базисной дугой, примыкающей к вершине, придаем направление, соответствующее знаку (для минуса дуга – входит в вершину, для плюса – выходит. Если =0, то любое). Величину потока по рассматриваемой дуге принимаем равной запасу или потребности груза в вершине. Пометки вершин,

соединенных этой дугой, уменьшаем на единицу, аа интенсивности у вершин корректируем с

учетом потока по дуге. Опять рассматриваем вершину с единичной пометкой и все действия повторяем. Процесс построения закончен, когда пометки у всех вершин – нулевые. В нашем случаем мы последовательно образовали базисные дуги 1-5; 4-5; 3-2; 5-3;

●​ Первый шаг метода потенциалов

Полученный базисный план должен быть проверен на оптимальность с помощью потенциалов, которые определяются так: произвольно выбранной вершине присваиваем любое значение в качестве потенциала. Двигаясь по базисным дугам, вычисляем потенциалы всех остальных вершин. Если дуга выходит из вершины, то к потенциалу вершины прибавляем

величину удельной стоимости этой дуги. Если дуга входит, то вычетается из

потенциала. Ниже, на рисунке, приведены значения вычисленных потенциалов, причем

построение было начато с потенциала первой вершины (значение 10)

●​ Второй шаг

Для определения оптимальности плана определим характеристики для всех небазисных

ребер. Каждому ребру инциденты два потенциала смежных вершин и . Тогда вычисляется как . Задача считается решенной, если план – оптимальный.

То есть характеристики всех небазисных ребер неотрицательны. Рассматриваемый план

(рисунок выше) – неоптимальный ( ) Переходим к следующему шагу.

●​ Третий шаг

Одно небазисное ребро с отрицательной характеристикой, например 1-2, введем в базис. Составим цикл, состоящий из этого ребра и базисных дуг; такой цикл – единственный и имеет вид 1-2, 3-2, 5-3, 1-5

●​ Четвертый шаг

Ориентируем ребро 1-2 в построенном цикле в направлении от вершины с меньшим потенциалом к вершине с большим потенциалом. В нашем случае к вершине 2. Рассмотрим цепь из базисных дуг, соединяющую конец дуги (1-2) с ее началом. То есть будем двигаться по этой цепи в направлении от вершины 2 к вершине 1. Среди всех базисных дуг, направление которых противоположно нашему движению (то есть противоположно нгаправлению новой дуги 1-2), выбираем базисную дугу с наименьшим значением потока на ней. На рисунке в П.1 среди дуг противоположного направления (3-2; 5-3; 1-5) выбираем дугу 1-5 с . Выполняем

перераспределение потоков (поставок груза) в дугах рассматриваемого цикла. Для этого найденная величина потока (20 единиц) прибавляется ко всем потокам в дугах цикла, совпадающих по направлению с новой дугой и вычитается из оптокоав в дугах цикла противоположного направления. После этого выбранная дуга 1-5 с наименьшим значением