Для максимизации:
30. Метод (де)Била.
Пусть дана функция:
С ограничениями 
Пусть нам удалось построить первое допустимое базисное решение (далее - ДБР) для этой
задачи (разделить переменные на обязательные и необязательные и выразить обязательные через необязательные), где
– обязательные
– необязательные
Далее можно решить обычным симплекс методом, но с учетом того, что когда первый (?кто первый?) обращается в нуль, какая-либо скобка при н\б переменной, то тогда вводится дополнительная неограниченная по знаку переменная 
равная содержимому этой скобки.
И разрешаем полученное уравнения относительно 
(приходит в число н\б переменных)
Небазисными будут являться все переменные, что и в первом ДБР (кроме 
- она придет к баз. и переменная 
(станет н\б))
Если 
, то значение 
надо увеличить
Если 
, то значение 
надо уменьшить
Если 
, то функция (1) достигла максимума по этой переменной (2) то переменная 
стала базисной
Полный алгоритм метода Била
1. Каким-либо образом получаем первое ДБР, если не удалось – значит искомая задача несовместна
2. Проверяем первую строку функции цели в нижней части таблицы. Если все
коэффициенты 
, все коэффициенты при переменной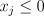 
, то текущее ДБР является оптимальным (конец решения). Иначе в качестве разрешающего столбца
выбираем любой столбец с |
|
с коэффициентом в строке не равной нулю. Если все |
|
коэффициенты при |
или таких столбцов нет, то разрешающим берем любой |
||
столбец, где коэффициенты при |
больше нуля (обозначим ) |
|
|
3. Вычисляем отношение |
к |
, если этот коэффициент |
, сравниваем это |
отношение с отношением из верхней части таблицы свободных членов к модулям коэффициентов из разрешающего столбца, знаки которых противоположны по знаку элементу 
. Строка, дающая минимум среди этих отношений, является разрешающей.
4. Заполнение промежуточной таблицы. В качестве заглавной переменной в разрешенном столбце ставим имя переменной из разрешенной строки начальной таблицы, если эта разрешающая строка находится в верхней части начальной таблицы. Иначе в качестве
такой заглавной переменной записываем очередную переменную . Элементы |
из |
разрешающего столбца начальной таблицы делятся на генеральный элемент |
и |
записывают в промежуточную таблицу, остальные элементы разрешающей строки становятся равны 0. Прочие элементы пересчитываются по обычному правилу прямоугольника.
5. Заполнение конечной таблицы. Верхняя часть полностью переписывается из промежуточной таблицы, на место второй разрешающей строки конечной таблицы записывается вторая разрешающая строка промежуточной таблицы, деленная на генеральный элемент. В качестве заглавной переменной второй разрешающей строки конечной таблицы записывается имя переменной из разрешающего столбца промежуточной таблицы. В качесте h-ой (любой другой) строки нижней части таблицы записывается соответствующая строка промежуточной таблица, из которой надо
вычесть вторую разрешащую строку конечной