Добавил:

vikoskokos Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Технология материалов и эпитаксиальных структур

Файл:

ИДЗ1_ТМИЭС

.pdf

Скачиваний:

Добавлен:

25.01.2025

Размер:

460.23 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра микро- и наноэлектроники

ОТЧЁТ по практическому заданию № 1

по дисциплине «Технология материалов и эпитаксиальных структур» Тема: Легирование кристаллов при выращивании методом Чохральского

Вариант №5

Студентка гр. 1283	____________________	Григорьева В.В.
Преподаватель	__________________________	Бобков А.А.

Санкт-Петербург

2024

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

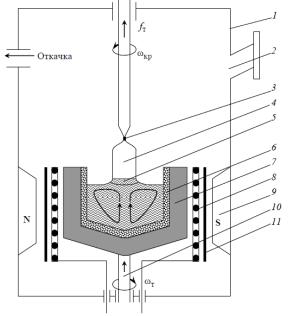
На рисунке 1 приведём схему установки для выращивания кристаллов

методом Чохральского.

Рисунок 1 – Схема установки для выращивания кристаллов методом Чохральского

	Элементы установки:
1.	Камера роста	2.	Смотровое окно
3.	Затравка	4.	Монокристалл
5.	Переохлаждённый столбик расплава	6.	Тигель из кварцевого стекла
7.	Графитовый стакан	8.	Резистивный нагреватель
9.	Источник магнитного поля	10.	Устройство подъёма и вращения тигля
11.	Тепловые экраны

Соотношения, используемые в расчётах.

Соотношение (1) – равновесный коэффициент распределения примеси – характеризует отношение концентрации примеси в твёрдой и жидкой фазах в условиях термодинамического равновесия.

где Ci тв

Ci ж

k0	=	Ci тв	,	(1)

		Ci ж

–концентрация примеси в твёрдой фазе,

–концентрация примеси в жидкой фазе.

Если скорость кристаллизации имеет конечное значение, то перед фронтом кристаллизации по мере роста кристалла образуется слой расплава с эффективной толщиной δ, обогащённый или обеднённый примесью, если k0

меньше или больше единицы соответственно.

В этих условиях содержание примеси в закристаллизовавшейся части слитка Ств будет определяться концентрацией примеси в расплаве у фронта кристаллизации Ств = k0Сж0. Значение Сж0, как правило, неизвестно, поэтому в неравновесных условиях связь между концентрациями примеси в твёрдой Ств

и жидкой Сж фазах осуществляют с помощью эффективного коэффициента распределения k, который задаётся выражением (2) – уравнение Бартона-

Прима-Слихтера, связывающее равновесный и эффективный коэффициенты распределения.

k =		k	0					,
k =								,

						−	f
k		+ (1− k			)e	−	D
k		+ (1− k			)e

	0			0

(2)

где f – скорость кристаллизации (0,5…5 мм/мин),

D – коэффициент диффузии примеси в жидкой фазе, см2/с,

δ – толщина диффузионного слоя, определяемая соотношением (3) (0,1…10-3 см).

1	1	−	1	(3)
= AD3 v 6			2 ,

где А – численный коэффициент, принимающий значения 1…2 (для МЧ – 1,6), v – кинематическая вязкость жидкости, см2/с,

ω – скорость вращения кристалла относительно тигля, рад/с.

Закон распределения примеси вдоль слитка – соотношение (4) –

уравнение Галливера:

C	тв	0	(	− g	)	k −1	,	(4)

		= kС	1

где g – доля закристаллизовавшегося расплава, равная отношению текущего и начального объёмов.

Приведённый коэффициент испарения имеет смысл в случае легирования кристалла летучей примесью, он определяется соотношением (5).

k		=	F	,
k	и	=	fS	,
	и

(5)

где S – площадь поперечного сечения кристалла – соотношение (6),

α – линейный коэффициент испарения (коэффициент межфазного взаимодействия),

F – площадь поверхности испарения, рассчитываемая с использованием соотношения (7).

			D
S		=	2	,
S		=	кр	,
			кр
	кр		4
			4

(6)

где Dкр – диаметр кристалла.

F =		(D	2	− D	2	),
			2		2
	4	т		кр
	4

(7)

где Dт – диаметр тигля.

Тогда имеет смысл ввести обобщённый коэффициент распределения,

учитывающий как эффективный коэффициент распределения, так и коэффициент испарения – соотношение (8).

k	об	= k + k	.	(8)
	об	и		(8)

Концентрация носителей заряда может быть рассчитана с использованием соотношений (9).

n =	1		,	p =	1	,
	e				e
		n				p

(9)

где е = 1,6 · 10-19 Кл, ρ – удельное сопротивление, которое может быть определено из марки

выращиваемого полупроводника,

μn и μp – подвижности электронов и дырок в полупроводнике при определённой температуре.

РАСЧЁТНАЯ ЧАСТЬ

Параметры, используемые в расчётах – таблица 1

Таблица 1 – Используемые значения параметров для Ge, легированного Ga, и для Ge,

легированного Sn

Материал	ν 103,	см2	k0 102	D 104,	см2	α 104,	см
							с
		с			с
		с			с

Ge − Ga	1,35		8,7	0,7		-

Ge − Sn			2	1,26		1,2
Ge − Sn			2	1,26		1,2

1. Построить зависимость Ств(g) для различных скоростей кристаллизации Ge, легированного Ga. Скорость вращения кристалла относительно тигля 60 об/мин. Скорость кристаллизации 0,5; 5; 10 мм/мин.

Начальная концентрация примеси в расплаве 1015 см-3. Построить график зависимости kэфф как функции скорости кристаллизации при скорости вращения кристалла относительно тигля 60 об/мин. Для указанных скоростей кристаллизации записать в таблицу значения kэфф.

Таблица 2 – Расчётные значения kэфф для различных скоростей кристаллизации

Скорость кристаллизации	0,5	5	10
f, мм/мин	0,5	5	10
f, мм/мин

kэфф · 103	95,63	212,54	433,26

1) Переведём заданные величины – скорости кристаллизации fi и

скорость вращения кристалла относительно тигля ω – в удобные для расчёта

единицы измерения:

об

2π рад

рад

ω = 60

= 60

≈ 6,283

мин

мм

10−1

см

≈ 8,33 10−4

см

f = 0,5

= 0,5

мин

мм

10−1 см

см

= 5

≈ 8,33 10−3

мин

мм

10−1 см

≈ 17 10−3

см

= 10

мин

ωkэфф(f) = 60

об

= 60

2π

рад

≈ 6,283

рад

мин

2) Рассчитаем значение толщины диффузионного слоя δ для первого случая – ω = 60 об/мин. Учтём, что для метода Чохральского – А = 1,6:

1	1	1	1	1	1	≈ 8,746 10−3см.
δ = AD3ν6ω−2			= 1,6 (0,7 ∙ 10−4)3	(1,35 10−3)6	(6,283)−2	≈ 8,746 10−3см.

3) Проведём расчет значений эффективного коэффициента распределения kэфф для различных значений скорости кристаллизации:

8,7 10−2

f1δ

−4

−3

эфф

+ (1 − k

)e−

8,7 10−2 + (1 − 8,7 10−2) exp (−

8,33 10

8,746 10

)

0,7 ∙ 10−4

≈ 0,09563,

8,7 10−2

f2δ

−3

эфф

+ (1 − k

)e−

8,7 10−2 + (1 − 8,7 10−2) exp (−

8,33 10

8,746 10

)

0,7 ∙ 10−4

≈ 0,21254,

8,7 10−2

f3δ

−3

эфф

+ (1 − k

)e−

8,7 10−2 + (1 − 8,7 10−2) exp (−

17 10

8,746 10

)

0,7 ∙ 10−4

≈0,43326.

4)Полученным значениям эффективного коэффициента

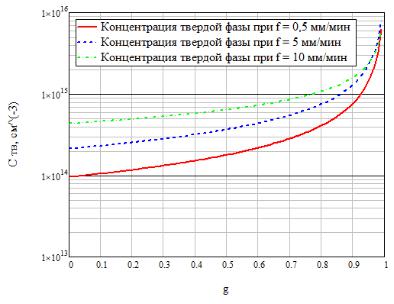
распределения сопоставим зависимости концентрации твёрдой фазы Ств(g) = kC0(1–g)k–1. Полученные зависимости аналитически представим на рисунке 1:

Рисунок 1 – График зависимостей концентрации твёрдой фазы от соотношения объёма

твёрдой фазы и полного объёма при различных скоростях кристаллизации

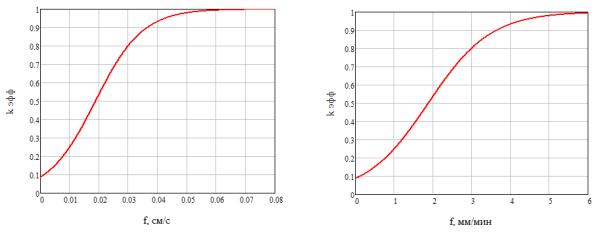
5) Построим график зависимости эффективного коэффициента распределения kэфф от скорости кристаллизации f при скорости вращения кристалла относительно тигля ω = 60 об/мин на рисунке 2:

а) б)

Рисунок 2 – Графики зависимостей эффективного коэффициента распределения от скорости кристаллизации при скорости вращения кристалла относительно тигля 60 об/мин

(а – скорость кристаллизации в см/с, б – скорость кристаллизации в мм/мин)

2. Построить зависимость Ств(g) для различных скоростей кристаллизации Ge, легированного Ga. Скорость кристаллизации 3 мм/мин.

Скорость вращения кристалла относительно тигля составляет 20; 50; 120

об/мин. Начальная концентрация примеси в расплаве 1015 см-3. Построить графики зависимости толщины диффузионного слоя δ и kэфф как функции скорости вращения кристалла относительно тигля при скорости кристаллизации 3 мм/мин. Для указанных скоростей кристаллизации записать в таблицу значения δ и kэфф.

Таблица 3 – Расчётные значения kэфф и δ для различных относительных скоростей вращения кристалла относительно тигля

ω, об/мин	20	50	120

kэфф · 103	219,454	158,889	129,081

δ, см	15,148 10−3	9,58 10−3	6,184 10−3

1) Переведём заданные величины – скорости кристаллизации fi и

скорость вращения кристалла относительно тигля ω – в удобные для расчёта единицы измерения:

мм

10−1 см

≈ 5 10−3

см

f = 3

= 3

мин

60 с

ω1

= 20

об

= 20

2π рад

≈ 2,094

рад

мин

ω2

= 50

об

= 50

2π рад

≈ 5,236

рад

мин

ω3 = 120

об

= 120

2π

рад

≈ 12,566

рад

мин

2) Рассчитаем значение толщин диффузионного слоя δ для всех случая. Учтём, что для метода Чохральского – А = 1,6:

δ		1 1		−1			1		1		1	≈ 15,148 10−3см,
δ	= AD3ν6ω				2	= 1,6 (0,7 ∙ 10−4)3		(1,35 10−3)6 (2,094)−2				≈ 15,148 10−3см,
1				1
δ		1	1		−1			1		1		1	≈ 9,58 10−3см,
δ	2	= AD3	ν6ω			2	= 1,6 (0,7 ∙ 10−4)3		(1,35 10−3)6		(5,236)−2		≈ 9,58 10−3см,
	2				2
δ		1 1		−1			1		1			1	≈ 6,184 10−3см.
δ	= AD3ν6ω				2	= 1,6 (0,7 ∙ 10−4)3		(1,35 10−3)6		(12,566)−2			≈ 6,184 10−3см.
2				3

3) Проведём расчет значений эффективного коэффициента

распределения kэфф для различных значений скорости кристаллизации:

8,7 10−2

−3

эфф

+ (1 − k

fδ1

8,7 10−2 + (1 − 8,7 10−2) exp (− 5 10

15,148 10

)e−

)

0,7 ∙ 10−4

≈ 0,21945,

8,7 10−2

fδ1

−3

эфф

+ (1 − k

8,7 10−2 + (1 − 8,7 10−2) exp (−

5 10

9,58 10

)e− D

)

0,7 ∙ 10−4

≈ 0,15889,

8,7 10−2

fδ1

−3

эфф

+ (1 − k

)e−

8,7 10−2 + (1 − 8,7 10−2) exp (− 5 10

6,184 10

)

0,7 ∙ 10−4

≈0,12908.

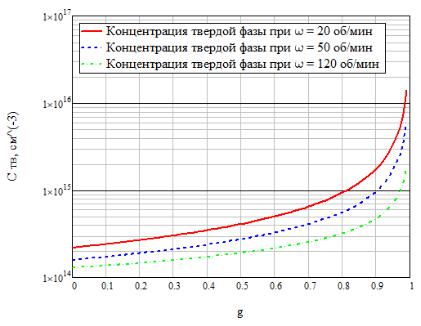
4)Полученным значениям эффективного коэффициента

Рисунок 3 – График зависимостей концентрации твёрдой фазы от соотношения объёма

твёрдой фазы и полного объёма при различных скоростях кристаллизации

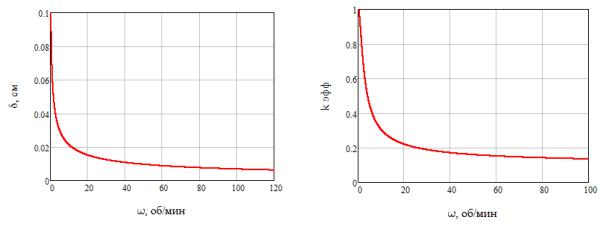
5) Построим график зависимости эффективного коэффициента распределения kэфф и диффузионного слоя δ от скорости вращения кристалла относительно тигля ω при скорости кристаллизации f = 3 мм/мин при на рисунке 2:

а) б)

Рисунок 4 – Графики зависимостей эффективного коэффициента распределения от скорости вращения кристалла относительно тигля при скорости кристаллизации 3 мм/мин

(а – толщина диффузионного слоя, б – эффективный коэффициент распределения)

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Технология материалов и эпитаксиальных структур

#
25.01.2025501.61 Кб6Задание №1. Метод Чохральского.xmcd
#
25.01.2025549.69 Кб8Зонная плавка.xmcd
#
25.01.2025460.23 Кб10ИДЗ1_ТМИЭС.pdf
#
25.01.2025569.36 Кб8ИДЗ2_ТМИЭС.pdf
#
25.01.2025352.4 Кб10Практическое задание №1.docx