МАТАН ЭКЗАМЕН / 31 / локальная ограниченность функции имеющей предел

Предел и непрерывность функции одной переменной

Теорема о локальной ограниченности функции, имеющей при  конечный предел

: ,

т.е. если функция при  имеет конечный предел, то существует окрестность точки , на которой множество значений функции  есть ограниченное числовое множество.

Доказательство. Поскольку к.ч., то для любого , в том числе для , существует  так, что для  , т.е. , где   или .

Заметим, что обратное утверждение неверно, т.е. если функция  локально ограничена на , то необязательно существует  и равен конечному значению.

Контрпример. Функция  имеет множество значений  – ограниченное множество в любой окрестности точки , но  не существует.

Заметим, что функция, имеющая в точке конечный предел, а значит, локально ограниченная в окрестности этой точки, может быть неограниченной на своей области существования. Например, ,  для .

Функция   бесконечно большая при  является неограниченной в любой окрестности . Обратное неверно, т.е. неограниченная в  функция  не обязательно бесконечно большая при . Например,  .

Частный случай (для последовательности):

всякая сходящаяся последовательность является ограниченной, т.е.

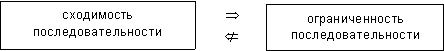Контрпример.   – ограниченная последователь-ность, но не является сходящейся, поскольку ее подпосле-довательности  и   сходятся к несовпадающим пределам.

Итак, теорема о локальной ограниченности является "односторонней" теоремой и выражает НЕОБХОДИМОЕ условие существования конечного предела функции (и последовательности).

Следующая серия утверждений описывает связь между соотношениями для функций и их пределов.