непрерывность функции

.docx

Скачиваний:

Добавлен:

17.03.2015

Размер:

73.22 Кб

Скачать

☆

Непрерывность функций

Определение непрерывности по Гейне

Говорят, что функция действительного переменного f (x) является непрерывной в точке ( - множество действительных чисел), если для любой последовательности , такой, что

выполняется соотношение

На практике удобно использовать следующие 3 условия непрерывности функции f (x) в точке x = a :

Функция f (x) определена в точке x = a;
Предел существует;
Выполняется равенство .

Определение непрерывности по Коши (нотация )

Рассмотрим функцию f (x), которая отображает множество действительных чисел на другое подмножествоB действительных чисел. Говорят, что функция f (x) является непрерывной в точке , если для любого числа существует число , такое, что для всех , удовлетворяющих соотношению

выполняется неравенство

Определение непрерывности в терминах приращений аргумента и функции

Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке x = a, если справедливо равенство

где . Приведенные определения непрерывности функции эквивалентны на множестве действительных чисел. Функция является непрерывной на данном интервале, если она непрерывна в каждой точке этого интервала.

Теоремы непрерывности

Теорема 1. Пусть функция f (x) непрерывна в точке x = a, и C является константой. Тогда функция Сf (x) также непрерывна при x = a. Теорема 2. Даны две функции f (x) и g (x), непрерывные в точке x = a. Тогда сумма этих функций f (x) + g (x) также непрерывна в точке x = a. Теорема 3. Предположим, что две функции f (x) и g (x) непрерывны в точке x = a. Тогда произведение этих функцийf (x) g (x) также непрерывно в точке x = a. Теорема 4. Даны две функции f (x) и g (x), непрерывные при x = a. Тогда отношение этих функций также непрерывно при x = a при условии, что . Теорема 5. Предположим, что функция f (x) является дифференцируемой в точке x = a. Тогда функция f (x) непрерывна в этой точке (т.е. из дифференцируемости следует непрерывность функции в точке; обратное − неверно). Теорема 6 (Теорема о предельном значении). Если функция f (x) непрерывна на закрытом и ограниченном интервале [a, b], то она ограничена сверху и снизу на данном интервале. Другими словами, существуют числа m и M, такие, что

для всех x в интервале [a, b] (смотрите рисунок 1).


Рис.1		Рис.2

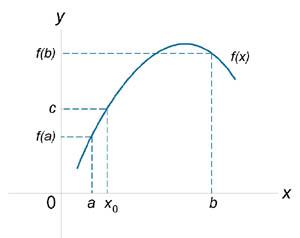
Теорема 7 (Теорема о промежуточном значении). Пусть функция f (x) непрерывна на закрытом и ограниченном интервале [a, b]. Тогда, если c − некоторое число, большее f (a) и меньшее f (b), то существует число x₀, такое, что

Данная теорема проиллюстрирована на рисунке 2.

Непрерывность элементарных функций

Все элементарные функции являются непрерывными в любой точке свой области определения. Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:
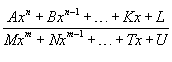