
ИДЗ
.pdf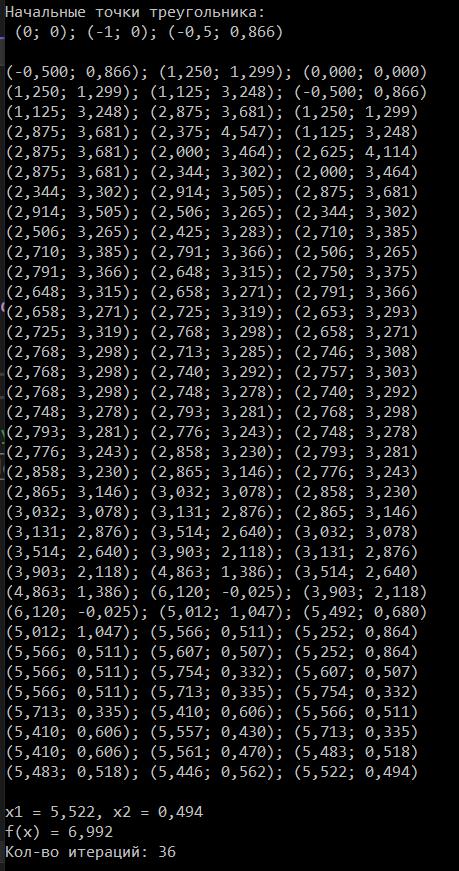
Рисунок 2.2.2– Работа программы для функции f5(x) методом Нелдера-Мида
21

По полученным данным можно построить общую траекторию спуска
(рисунок 2.2.3)
Рисунок 2.2.3 – Траектория спуска для функции f5(x) методом Нелдера-Мида
Рисунок 2.2.4 – Работа программы для функции f5(x) методом Быстрого спуска последние итерации
22

Рисунок 2.2.5 – График программы для функции f5(x) методом Быстрого спуска
Все необходимые данные и значения занесены в таблицу 2.2.
Таблица 2.2 – Результаты
|
Полученная |
Начальная точка |
Число итераций, |
|
точка |
(или отрезок) |
за которые |
|
минимума |
|
найден |
|
|
|
минимум |
|
|
|
|
метод Нелдера-Мида |
(5,522; 0,494) |
(0; 0); (-1; 0); |
36 |
|
|
(-0,5; 0,866) |
|
|
|
|
|
метод быстрого |
(6,8; -0,8) |
(18; 10) |
53 |
спуска |
|
|
|
|
|
|
|
23
Заключение
В ходе выполнения данной работы были изучены и применены на практике методы золотого сечения и дихотомии для минимизации одномерных функций, а также методы наискорейшего спуска и Нелдера-
Мида для минимизации многомерных функций с особенностью применения градиентного метода для минимизации многомерной функции.
24
Приложение А
Код программы для метода золотого сечения и дихотомии
using System; namespace Lab1_1
{
internal class Program
{
static void Main(string[] args)
{
int N = 0; double A = 0; double Y = 0;
List<double> xf1 = new List<double>(); List<double> xf2 = new List<double>(); List<double> xf3 = new List<double>(); List<double> yf1 = new List<double>(); List<double> yf2 = new List<double>(); List<double> yf3 = new List<double>();
Console.WriteLine("ЗОЛОТОЕ СЕЧЕНИЕ");
Console.WriteLine("\nПервая функчия");
GoldenRatio(FirstFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1); Console.Write($"Входная тоцка: *A+, Минимальное знацение функчии = *Y+ Число итерачий: * N+\n");
A = Y = 0; N = 0; xf1.Clear(); yf1.Clear(); Console.WriteLine("\nВторая функчия");
GoldenRatio(SecondFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1); Console.Write($"Входная тоцка: *A+, Минимальное знацение функчии = *Y+ Число итерачий: * N+\n");
A = Y = 0; N = 0; xf1.Clear(); yf1.Clear(); Console.WriteLine("\nТретья функчия");
GoldenRatio(ThirdFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1); Console.Write($"Входная тоцка: *A+, Минимальное знацение функчии = *Y+ Число итерачий: * N+\n");
A = Y = 0; N = 0; xf1.Clear(); yf1.Clear();
Console.WriteLine("МЕТОД ДИХОТОМИИ");
Console.WriteLine("\nПервая функчия");
DihMeth(FirstFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2);
Console.Write($"Входная тоцка: *A+, Минимальное значение функчии = *Y+ Число итерачий: * N+\n");
A = Y = 0; N = 0; xf2.Clear(); yf2.Clear(); Console.WriteLine("\nВторая функчия");
DihMeth(SecondFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2);
Console.Write($"Входная тоцка: *A+, Минимальное знацение функчии = *Y+ Число итерачий: * N+\n");
A = Y = 0; N = 0; xf2.Clear(); yf2.Clear(); Console.WriteLine("\nТретья функчия");
DihMeth(ThirdFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2);
Console.Write($"Входная тоцка: *A+, Минимальное знацение функчии = *Y+ Число итерачий: * N+\n");
A = Y = 0; N = 0; xf2.Clear(); yf2.Clear();
}
static Operation FirstFunction()
{
double GetFunction(double x)
{
return 4 - 9 * Math.Exp(-Math.Pow(x - 3, 2));
}
return GetFunction;
}
static Operation SecondFunction()
25
{
double GetFunction(double x)
{
return 5 * (x - 2) * (x - 3) * (x - 1);
}
return GetFunction;
}
static Operation ThirdFunction()
{
double GetFunction(double x)
{
return x/5 + Math.Sin(5 * 3.14 * x + 2);
}
return GetFunction;
}
static (double, double, int) GoldenRatio(Operation Function, double a, double b, ref int N, ref double A, ref double Y, ref List<double> xf1, ref List<double> yf1)
{
double XB, XA;
const double Alph = 0.618; const double Bet = 0.382; while (Math.Abs(a - b) > 0.0001)
{
XB = a + Bet * Math.Abs(a - b); XA = a + Alph * Math.Abs(a - b); if (Function(XB) > Function(XA))
{
a = XB;
}
else
{
b = XA;
}
N++;
if (Function(a) < Function(b))
{
A = a; xf1.Add(a);
Y = Function(a); yf1.Add(Y);
}
else
{
A = b; xf1.Add(a);
Y = Function(b); yf1.Add(Y);
}
Console.WriteLine("{0}\t{1:F5}\t{2:F5}", N, A, Y);
}
if (Function(a) < Function(b))
{
A = a;
Y = Function(a); return (A, Y, N);
}
else
{
A = b;
Y = Function(b); return (A, Y, N);
}
}
static (double, double, int) DihMeth(Operation Function, double a, double b, ref int N, ref double A, ref double Y, ref List<double> xf2, ref List<double> yf2)
{
double Sigma = 0.00001; double X1; double X2;
while (Math.Abs(a - b) >= 0.0001)
{
X1 = (a + b - Sigma) / 2;
26
X2 = (a + b + Sigma) / 2;
if (Function(X1) > Function(X2))
{
a = X1;
}
else
{
b = X1;
}
N++;
A = (a + b) / 2; xf2.Add(A); Y = Function(a); yf2.Add(Y);
Console.WriteLine("{0}\t{1:F5}\t{2:F5}", N, A, Y);
}
A = (a + b) / 2; Y = Function(a); return (A, Y, N);
}
static (double, double, int) FibonachiMethod(Operation Function, double a, double b, ref int N, ref double A, ref double Y, ref List<double> xf3, ref List<double> yf3)
{
double X1, X2; int k, n = 0; k = 1;
long usl = Convert.ToInt64(NumberFib(1));
for (int i = 1; usl < (Math.Abs(a - b) / 0.0001); i++, n = i - 1) usl = Convert.ToInt64(NumberFib(i));
while (Math.Abs(a - b) >= 0.0001)
{
X1 = a + (NumberFib(n - k + 1) / NumberFib(n - k + 3) * (b - a)); X2 = a + (NumberFib(n - k + 2) / NumberFib(n - k + 3) * (b - a)); if (Function(X1) >= Function(X2))
{
a = X1; k++;
}
else
{
b = X2; k++;
}
N++;
A = (a + b) / 2; xf3.Add(A);
Y = Function((a + b) / 2); yf3.Add(Y); Console.WriteLine("{0}\t{1:F5}\t{2:F5}", N, A, Y);
}
A = (a + b) / 2;
Y = Function((a + b) / 2); return (A, Y, N);
}
static double NumberFib(int num)
{
return Convert.ToInt64((Math.Pow((1 + Math.Sqrt(5)) / 2, num) - Math.Pow((1 - Math.Sqrt(5)) / 2, num)) / Math.Sqrt(5));
}
delegate double Operation(double g); delegate int Operati(int n);
}
}
27
Приложение Б
Код программы для метода Нелдера-Мида
double Function_4(double x1, double x2)
{
double func = (9 * (x1 - 1) * (x1 - 1) + 5 * (x2 - 3) * (x2 - 3)); return func;
}
double Function_5(double x1, double x2)
{
double func = Math.Pow((x1 - 6), 2) + Math.Pow((x2 - 1), 2) + 30 * Math.Pow((x2 + x1 - 6), 2) + 6.5; //Math.Pow((x1 - 1), 2) + Math.Pow((x2 - 1), 2) + (50 * Math.Pow((x2 + (3 * x1) - 6), 2)) + 8.3;
return func;
}
double[] SearchMinF4(double[] x_1, double[] x_2, double[] x_3)
{
if (((Function_4(x_1[0], x_1[1]) < Function_4(x_2[0], x_2[1])) && (Function_4(x_1[0], x_1[1]) < Function_4(x_3[0], x_3[1]))) ||
((Function_4(x_1[0], x_1[1]) == Function_4(x_2[0], x_2[1])) && (Function_4(x_1[0], x_1[1]) < Function_4(x_3[0], x_3[1]))) ||
((Function_4(x_1[0], x_1[1]) == Function_4(x_3[0], x_3[1])) && (Function_4(x_1[0], x_1[1]) < Function_4(x_2[0], x_2[1]))))
return x_1;
if (((Function_4(x_2[0], x_2[1]) < Function_4(x_1[0], x_1[1])) && (Function_4(x_2[0], x_2[1]) < Function_4(x_3[0], x_3[1]))) ||
((Function_4(x_2[0], x_2[1]) == Function_4(x_1[0], x_1[1])) && (Function_4(x_2[0], x_2[1]) < Function_4(x_3[0], x_3[1]))) ||
((Function_4(x_2[0], x_2[1]) == Function_4(x_3[0], x_3[1])) && (Function_4(x_2[0], x_2[1]) < Function_4(x_1[0], x_1[1]))))
return x_2; return x_3;
}
double[] SearchMaxF4(double[] x_1, double[] x_2, double[] x_3)
{
if (((Function_4(x_1[0], x_1[1]) > Function_4(x_2[0], x_2[1])) && (Function_4(x_1[0], x_1[1]) > Function_4(x_3[0], x_3[1]))) ||
((Function_4(x_1[0], x_1[1]) == Function_4(x_2[0], x_2[1])) && (Function_4(x_1[0], x_1[1]) > Function_4(x_3[0], x_3[1]))) ||
((Function_4(x_1[0], x_1[1]) == Function_4(x_3[0], x_3[1])) && (Function_4(x_1[0], x_1[1]) > Function_4(x_2[0], x_2[1]))))
return x_1;
if (((Function_4(x_2[0], x_2[1]) > Function_4(x_1[0], x_1[1])) && (Function_4(x_2[0], x_2[1]) > Function_4(x_3[0], x_3[1]))) ||
((Function_4(x_2[0], x_2[1]) == Function_4(x_1[0], x_1[1])) && (Function_4(x_2[0], x_2[1]) > Function_4(x_3[0], x_3[1]))) ||
((Function_4(x_2[0], x_2[1]) == Function_4(x_3[0], x_3[1])) && (Function_4(x_2[0], x_2[1]) > Function_4(x_1[0], x_1[1]))))
return x_2; return x_3;
}
double[] SearchMedF4(double[] x_1, double[] x_2, double[] x_3)
{
if ((SearchMinF4(x_1, x_2, x_3) == x_1 && SearchMaxF4(x_1, x_2, x_3) ==
x_2) || (SearchMinF4(x_1, x_2, x_3) == x_2 && SearchMaxF4(x_1, x_2, x_3) == x_1)) return x_3;
if ((SearchMinF4(x_1, x_2, x_3) == x_1 && SearchMaxF4(x_1, x_2, x_3) ==
x_3) || (SearchMinF4(x_1, x_2, x_3) == x_3 && SearchMaxF4(x_1, x_2, x_3) == x_1)) return x_2;
return x_1;
}
28
double[] SearchMinF5(double[] _x1, double[] _x2, double[] _x3)
{
if (((Function_5(_x1[0], _x1[1]) < Function_5(_x2[0], _x2[1])) && (Function_5(_x1[0], _x1[1]) < Function_5(_x3[0], _x3[1]))) ||
((Function_5(_x1[0], _x1[1]) == Function_5(_x2[0], _x2[1])) && (Function_5(_x1[0], _x1[1]) < Function_5(_x3[0], _x3[1]))) ||
((Function_5(_x1[0], _x1[1]) == Function_5(_x3[0], _x3[1])) && (Function_5(_x1[0], _x1[1]) < Function_5(_x2[0], _x2[1]))))
return _x1;
if (((Function_5(_x2[0], _x2[1]) < Function_5(_x1[0], _x1[1])) && (Function_5(_x2[0], _x2[1]) < Function_5(_x3[0], _x3[1]))) ||
((Function_5(_x2[0], _x2[1]) == Function_5(_x1[0], _x1[1])) && (Function_5(_x2[0], _x2[1]) < Function_5(_x3[0], _x3[1]))) ||
((Function_5(_x2[0], _x2[1]) == Function_5(_x3[0], _x3[1])) && (Function_5(_x2[0], _x2[1]) < Function_5(_x1[0], _x1[1]))))
return _x2; return _x3;
}
double[] SearchMaxF5(double[] _x1, double[] _x2, double[] _x3)
{
if (((Function_5(_x1[0], _x1[1]) > Function_5(_x2[0], _x2[1])) && (Function_5(_x1[0], _x1[1]) > Function_5(_x3[0], _x3[1]))) ||
((Function_5(_x1[0], _x1[1]) == Function_5(_x2[0], _x2[1])) && (Function_5(_x1[0], _x1[1]) > Function_5(_x3[0], _x3[1]))) ||
((Function_5(_x1[0], _x1[1]) == Function_5(_x3[0], _x3[1])) && (Function_5(_x1[0], _x1[1]) > Function_5(_x2[0], _x2[1]))))
return _x1;
if (((Function_5(_x2[0], _x2[1]) > Function_5(_x1[0], _x1[1])) && (Function_5(_x2[0], _x2[1]) > Function_5(_x3[0], _x3[1]))) ||
((Function_5(_x2[0], _x2[1]) == Function_5(_x1[0], _x1[1])) && (Function_5(_x2[0], _x2[1]) > Function_5(_x3[0], _x3[1]))) ||
((Function_5(_x2[0], _x2[1]) == Function_5(_x3[0], _x3[1])) && (Function_5(_x2[0], _x2[1]) > Function_5(_x1[0], _x1[1]))))
return _x2; return _x3;
}
double[] SearchMedF5(double[] _x1, double[] _x2, double[] _x3)
{
if ((SearchMinF5(_x1, _x2, _x3) == _x1 && SearchMaxF5(_x1, _x2, _x3) ==
_x2) || (SearchMinF5(_x1, _x2, _x3) == _x2 && SearchMaxF5(_x1, _x2, _x3) == _x1)) return _x3;
if ((SearchMinF5(_x1, _x2, _x3) == _x1 && SearchMaxF5(_x1, _x2, _x3) ==
_x3) || (SearchMinF5(_x1, _x2, _x3) == _x3 && SearchMaxF5(_x1, _x2, _x3) == _x1)) return _x2;
return _x1;
}
double LimitF4(double[] x_max, double[] x_min, double[] x_med, double[] x_cen)
{
double sum = Math.Pow((Function_4(x_max[0], x_max[1]) - Function_4(x_cen[0], x_cen[1])), 2);
sum += Math.Pow((Function_4(x_med[0], x_med[1]) - Function_4(x_cen[0], x_cen[1])), 2);
sum += Math.Pow((Function_4(x_min[0], x_min[1]) - Function_4(x_cen[0], x_cen[1])), 2);
sum = sum / 3;
double result = Math.Sqrt(sum); return result;
}
double LimitF5(double[] xmax, double[] xmin, double[] xmed, double[] xcen)
{
double sum = Math.Pow((Function_5(xmax[0], xmax[1]) - Function_5(xcen[0], xcen[1])), 2);
sum += Math.Pow((Function_5(xmed[0], xmed[1]) - Function_5(xcen[0],
29
xcen[1])), 2);
sum += Math.Pow((Function_5(xmin[0], xmin[1]) - Function_5(xcen[0], xcen[1])), 2);
sum = sum / 3;
double result = Math.Sqrt(sum); return result;
}
double[] x1 = { 0, 0 }; double[] x2 = { -1, 0 };
double[] x3 = { -0.5, (Math.Sqrt(3) / 2) }; Console.WriteLine("1. f(x) = 9 * (x1 - 1)^2 + 5 * (x2 - 3)^2");
Console.WriteLine("2. f(x) = (x1 − 6)^2 + (x2 − 1)^2 + 30 * (x2 + x1 − 6)^2 + 6,5");
Console.WriteLine("Введите номер функчии, которую хотите решить:"); int choice = int.Parse(Console.ReadLine());
switch (choice)
{
case 1:
Console.WriteLine("Нацальные тоцки треугольника:");
Console.WriteLine($"({x1[0]}; {x1[1]}); ({x2[0]}; {x2[1]}); ({x3[0]}; {x3[1]:F3})");
Console.WriteLine(); int count = 0;
double[] xmax = SearchMaxF4(x1, x2, x3); double[] xmin = SearchMinF4(x1, x2, x3); double[] xmed = SearchMedF4(x1, x2, x3); double[] xcen = new double[2];
xcen[0] = ((xmin[0] + xmed[0]) / 2); xcen[1] = ((xmin[1] + xmed[1]) / 2); while (LimitF4(xmax, xmin, xmed, xcen) > 0.01)
{
double[] x1_ = new double[2]; double[] x2_ = new double[2]; double[] x3_ = new double[2]; double[] xotr = new double[2];
xotr[0] = xcen[0] + (xcen[0] - xmax[0]); xotr[1] = xcen[1] + (xcen[1] - xmax[1]);
if (Function_4(xotr[0], xotr[1]) < Function_4(xmin[0], xmin[1]))
{
double[] xras = new double[2];
xras[0] = xcen[0] + (2 * (xotr[0] - xcen[0])); xras[1] = xcen[1] + (2 * (xotr[1] - xcen[1]));
if (Function_4(xras[0], xras[1]) < Function_4(xmin[0], xmin[1]))
{
xmax[0] = xras[0]; xmax[1] = xras[1];
}
else
{
xmax[0] = xotr[0]; xmax[1] = xotr[1];
}
}
else
{
if (Function_4(xotr[0], xotr[1]) > Function_4(xmed[0], xmed[1]))
{
if (Function_4(xotr[0], xotr[1]) > Function_4(xmax[0], xmax[1]))
{
xmed[0] = xmin[0] + (0.5 * (xmed[0] - xmin[0])); xmed[1] = xmin[1] + (0.5 * (xmed[1] - xmin[1])); xmax[0] = xmin[0] + (0.5 * (xmax[0] - xmin[0])); xmax[1] = xmin[1] + (0.5 * (xmax[1] - xmin[1]));
30
