
ИДЗ
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-
вычислительных систем (КИБЭВС)
««Минимизация функций без ограничений на переменные» Отчет по индивидуальному домашнему заданию
по дисциплине «Методы оптимизации»
Студент гр. 723-1
_________Лысенко Е.М.
__________
Принял
Ст. преподаватель
кафедры КИБЭВС
________ Катаева Е.С.
__________
Томск 2024
Содержание
Введение................................................................................................................... |
3 |
ХОД РАБОТЫ ......................................................................................................... |
4 |
1. Одномерная оптимизация без ограничений................................................... |
4 |
1.1 Минимизация одномерной функции f1(x) .................................................. |
4 |
1.2 Минимизация одномерной функции f2(x) .................................................. |
8 |
1.3 Минимизация одномерной функции f3(x) ................................................ |
12 |
2. Многомерная оптимизация без ограничений .............................................. |
16 |
2.1 Минимизация одномерной функции f4(x) ............................................. |
16 |
2.2Минимизация одномерной функции f5(x) ................................................. |
20 |
Заключение ............................................................................................................ |
24 |
Приложение А ....................................................................................................... |
25 |
Приложение Б ........................................................................................................ |
28 |
Приложение В........................................................................................................ |
34 |
2
Введение
Целью работы является разработать программы, реализующие метод золотого сечения, метод дихотомии, метод Нелдера-Мида и метод наискорейшего спуска.
С помощью полученных программ нужно найти точки минимума и значения минимума для пяти функций
3
ХОД РАБОТЫ
1. Одномерная оптимизация без ограничений
1.1 Минимизация одномерной функции f1(x)
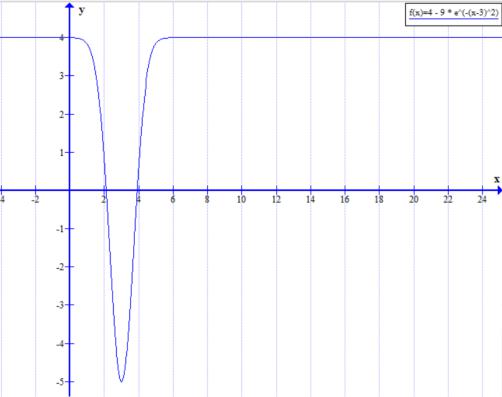
Функция f1(x) задана формулой 1.1.1
(1.1.1)
График функции представлен на рисунке 1.1.1.
Рисунок 1.1.1 – График функции f1(x)
Результат работы программы представлен на рисунке 1.1.2-1.1.4.
4

Рисунок 1.1.2 – Результат работы программы для функции f1(x) методом Золотого сечения
Рисунок 1.1.3 – График работы программы для функции f1(x) методом Золотого сечения
5

Рисунок 1.1.4 – Результат работы программы для функции f1(x) методом Дихотомии
Рисунок 1.1.5 – График работы программы для функции f1(x) методом Дихотомии
Все необходимые данные и значения занесены в таблицу 1.1.
6
Таблица 1.1 – Результаты
|
Полученная |
Начальная точка |
Число итераций, |
|
точка |
(или отрезок) |
за которые |
|
минимума |
|
найден |
|
|
|
минимум |
|
|
|
|
метод Золотого |
-4,999999995 |
3,00002303296549 |
24 |
сечения |
|
|
|
|
|
|
|
метод Дихотомии |
-4,999999996 |
3,00001696445465 |
17 |
|
|
|
|
7

1.2 Минимизация одномерной функции f2(x)
Функция f2(x) задана формулой 1.2.1
(1.2.1)
График функции представлен на рисунке 1.2.1.
Рисунок 1.2.1 – График функции f2(x)
Результат работы программы представлен на рисунке 1.2.2.
8

Рисунок 1.2.2 – Результат работы программы для функции f2(x) методом Золотого сечения
Рисунок 1.2.3 – График работы программы для функции f2(x) методом Золотого сечения
9

Рисунок 1.2.4 – Результат работы программы для функции f2(x) методом Дихотомии
Рисунок 1.2.5 – График работы программы для функции f2(x) методом Дихотомии
Все необходимые данные и значения занесены в таблицу 1.2.
10
