Формирование дискретной случайной величины с равновероятным распределением
При моделировании случайных величин формируется сначала случайная величина с простым законом распределения, а затем, на её основе, формируется желаемая для нас случайная величина (рис.3)
Рис.3 – Формулы моделирования случайных величин с равновероятным распределением
Сначала, формируем случайную величину, расположенную в интервале [0:1], установим порог = 0.5 и затем сравниваем выборочное значение x с порогом. В программе MathLab это будет выглядеть следующим образом:
x=rand (1);
if x>= 0,5:
Teta = 1
else:
Teta = 0
end;
При однократном запуске данного кода мы получаем одно значение величины Teta – либо 0 либо 1.
Формирование дискретной случайной величины с не равновероятным распределением
Рис.4 – Формулы моделирования случайных величин с не равновероятным распределением
При формировании кода программы в MathLab мы меняем порог, в результате чего код станет таким:
x=rand (1);
if x >= Po:
Teta = 1
else:
Teta = 0
end;
При множественном запуске этой программы мы получаем последовательность двоичных случайных величин с заданной вероятностью появление 0.
Формирование дискретной случайной величины с не равновероятным распределением и с числом значений больше 2
Рис.5 – Формулы моделирования случайных величин с не равновероятным распределением и с числом значений больше 2
Код программы в MathLab будет выглядеть следующим образом:
x=rand (1);
if x <= P2:
Teta = 2
else:
if x <= p2+ p1:
Teta = 1
else:
Teta = 0
end;
end;
3 Лекция (02.10.2024) Тема: «Моделирование гауссовской случайной величины»
Рис.6 – График и формула распределения гауссовской случайной величины
В системе MathLab есть отдельный датчик, который генерирует выборочное случайное значение гауссовской случайной величины. Написание данного датчика представлено на рис.7.
Рис.7 – Датчик генерации выборочного случайного значения гауссовской случайной величины
Обращение к данному датчику даёт значение гауссовской случайной величины с нулевым математическим ожиданием и с дисперсией, равными 1.
Моделирование (формирование)
Задача:
Необходимо
сформировать гауссовскую случайную
величину с заданными математическим
ожиданием и дисперсией, равными
.
Исходя
из того, что X
– гауссовская случайная величина,
которая имеет mx=0
и
,
а Y
= d*X
+
– другая гауссовская случайная величина,
найдём математическое ожидание mY
и дисперсию случайной величины δ2Y
(рис.8).
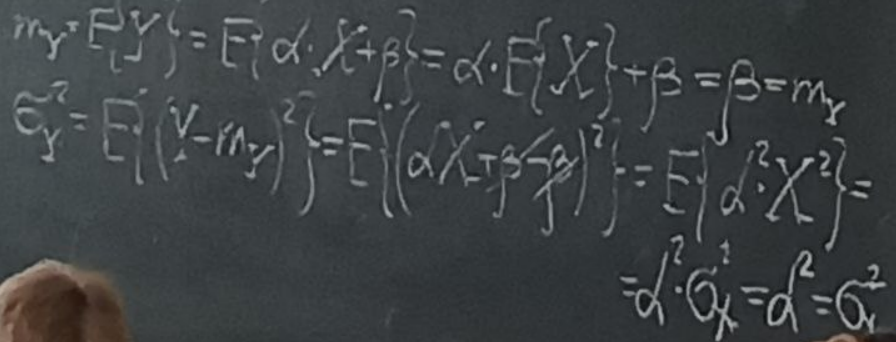
Рис.8 – Нахождение математического ожидания и дисперсии случайной величины
Отсюда следуют выражения, представленные на рис.9.
Рис.9 – Продолжение решения задачи
Данное распределение имеет ошибки измерений, шумы или помехи в различных технических системах. Причиной этого является центральная предельная теорема (ЦПТ), которая может быть сформулирована следующим образом: Распределение суммы большого числа независимых случайных величин при весьма общих условиях близко к нормальному закону распределению.