КонтрольнаяВариант3

Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования

«Волгоградский государственный технический университет» Кировский вечерний факультет

Кафедра «Физика»

Контрольная работа

по физике Вариант № 3

Выполнил (а)

_{Студент} (ка) группы

^Ф.И.О. Sol Invictus

Проверил: доцент, к.ф.-м.н..

(должность, степень, Ф.И.О.)

Результат проверки:

(оценка, дата, подпись преподавателя)

Волгоград 202*

1. Найти плотность тока, текущего по проводнику длиной 5 м, если на его концах поддерживается разность потенциалов 2 В. Удельное сопротивление материала проводника 210^-6 Омм.

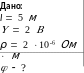^{Решение. Плотность тока равна:} j  ^{I .}

S

U ρl

^{По закону Ома:} I 

US

^{, где} R 

R S

U

- сопротивление провода.

^{Значит,} I 

. Тогда,

2

ρl

j  _ρl ^.

Получаем,

^{j } 2 10^6  5

 2 10^{5 А .}

_м2

Ответ.

j  2 10^{5 А .}

_м2

2. Падение напряжения во внешней цепи равно 5,1 В. Определить ток в цепи, ЭДС и КПД источника тока, если его внутреннее сопротивление 1,5 Ом, а сопротивление внешней цепи 8,5 Ом.

Решение.

I

U

Падение напряжения во внешней цепи равно: U  IR . Значит, сила тока в цепи равна: I  .

R

Сила тока по закону Ома для полной цепи равна: I 

ε

R  r ^.

ε

Значит, ЭДС источника равен:

 ^U  ε 

U _ R  r _

.

R  r R R

КПД источника равен: η 

W_R

W_R  W_r

100% ,

где W_R  I ²R - мощность, выделяемая во внешнем сопротивлении;

W_r  I ²r - мощность, выделяемая внутри элемента.

I ²R R

Значит, для КПД имеем: η  _{I 2 R  I 2r} 100%  _{R  r} 100% .

5,1

^5,1 ^{8,5 1,5}

8,5

Получаем, I   0, 6 А, ε   6 В , η  100%  85%.

8,5

Ответ. I  0,6 А , ε  6 В , η  85%.

8,5

8,5  1,5

3. ЭДС батареи 80 В, внутреннее сопротивление 5 Ом. Внешняя цепь потребляет мощность 100 Вт. Определить силу тока в цепи, напряжение, под которым находится внешняя цепь и ее сопротивление.

Решение. Мощность во внешней цепи: P  I ²R .

ε

Закон Ома для замкнутой цепи I  .

R  r

Значит,

_ε 2

2

^{I } R²  2rR  r ^{2 .}

ε ²R

Тогда, P  _{ 2rR  r} .

_R2 2

Значит, PR²  2RrP  r ²P  ε ²R .

Подставим числовые значения: 100R²  2 100  5  R  100  25²  80² R ,

100R²  5400R  62500  0 .

Разделим все на 100: R²  54R  625  0 .

54  54²  4  625 54  20, 4

Решаем квадратное уравнение: R_1,2  ₂  ₂

Тогда, R₁  37, 2 Ом , R₂  16,8 Ом .

ε ε

Значит,

I₁ 

R

1

• r ^,

I₂ 

R

2

• r ^.

80

80

Получаем, I₁  _{37, 2  5}  1,896 A , I₂  _{16,8  5}  3,67 A .

Напряжение равно: U₁  I₁R₁ , U₂  I₂ R₂ .

Получаем, U₁  1,896  37, 2  70,531 B , U₂  3, 67 16,8  61,656 B .

Ответ. R₁  37, 2 Ом , R₂  16,8 Ом , I₁  1,896 A , I₂  3,67 A , U₁  70,531 B ,

U₂  61,656 B .

4. Магнитный момент тонкого проводящего кольца 5 А·м². Определить магнитную индукцию в точке A, находящейся на оси кольца и удаленной от точке кольца на расстояние 20 см.

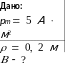Решение.

dB_

A

_pm

O

I

dB

dB

r

_β α

^R dl





→

 

По закону Био-Савара-Лапласа:

→ _μ

dB  ⁰

4π

I dl , r

_{r 2} ,

где dB - магнитная индукция поля, создаваемая элементом тока Idl в точке,

определяемой вектором r , μ₀

 4π 10^7

Гн

- магнитная постоянная.

м

Выделим на кольце элемент dl и от него в точку A проведем радиус-вектор r . Вектор

dB направим в соответствии правилом буравчика.

Согласно принципу суперпозиции магнитного поля, магнитная индукция в точке A

определяется интегрированием: B  _ dB , где интегрирование ведется по всем элементам

l

dl кольца.

Разложим вектор dB на две составляющие: dB_ , перпендикулярную плоскости кольца и

dB параллельную.

Тогда, B  _ dB_  _ dB .

l l

_ dB  0 из соображений симметрии, векторы dB_ от различных элементов dl

l

сонаправлены, поэтому заменяем векторное суммирование скалярным:

_B  _ dB_

, где

dB_

 dB cos β

→ _μ

и dB  ⁰

4π

Idl

_r2 , так как dl перпендикулярно r и

l

sinα  1.

Значит, B 

^μ0 I cos β 2π R dl  ^{2π Rμ0} I cos β .

R

4πr ²

Так как cos β  , то



0

B  ^μ

0

IR²

3

4πr²

.

r

Магнитный момент равен:

2r

p_m  IS , где S  π R²

- площадь витка.

Тогда,

B  ^{μ0 pm} .

2πr³

4π 10^7  5 _4

Получаем, B   1, 25 10 Тл .

^{2π } ^{0, 2}³

Ответ. B  1, 25 10^4 Тл .

5. Ион, пройдя ускоряющую разность потенциалов 645 В, влетел в скрещенные под прямым углом однородные магнитное (1,5 мТл) и электрическое (200 В/м) поля. Определить отношение заряда иона к его массе, если ион в этих полях движется прямолинейно.

Дано:

U  645 B

B  1,5 10^3 Тл

В

Решение.

E  200

м

^q  ?

m

Сила Лоренца со стороны магнитного поля: F_Л  qυ B .

Сила Кулона со стороны электрического поля: F_К  qE .

По второму закону Ньютона имеем: 0  F_Л  F_K .

_E

В проекции на ось x имеем: 0  F_Л  F_K  F_Л

Значит, qE  qυ B  υ  .

B

 F_K .

mυ ²

Пройдя ускоряющую разность потенциалов, ион приобретает энергию: qU  .

2

Значит,

q E ²

^m 2UB^{2 .}





q

200² ₇ Кл

Получаем,

^m 2  645  _1,5 10^3 _2

 1,38 10 .

кг

q Кл

Ответ.  1,38 10⁷ .

m кг

6. В однородном магнитном поле с индукцией 0,5 Тл вращается с частотой 10 c^-1 стержень длиной 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определить разность потенциалов на концах стержня.

Решение.

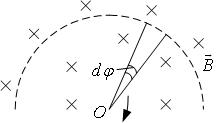
_{Индуцируемая} ЭДС: _εi

_{ } d _.

dt

^{Магнитный поток равен:}   BS cosα ^{, где} α  0 ^{- угол между вектором магнитной}

^{индукции} и вектором нормали контура, образуемым стрежнем при вращении. ^{Значит,}   BS ^.

Тогда, _{ε  B} ^dS , где dS - площадь, описываемая стержнем при вращении.

i

_Имеем: _{dS }

dt

l

2

dφ ^.

2

_l2

^{Так как} dφ  ωdt ^{, то имеем:} _{dS }

ωdt ^.

2

dS d

^ l ²

^ Bl ²ω

_ 

^{Так как} ε_i

 U ^{, то имеем:} _{U  B}

dt

 B _{dt  2} ωdt _  ₂ ^.

^{Угловая скорость равна:} ω  2πn ^.

Bl ² 2πn

_{Значит, U}

  πnBl^{2 .}

2

^{Получаем,} U  3,14 10  0,5  _0, 2_2  0,63 B ^.

^Ответ. U  0, 63 B ^.

7. На мыльную пленку падает белый свет под углом 60º. При какой наименьшей толщине пленки отраженные лучи будут окрашены в красный цвет (0,65 мкм)? Показатель преломления мыльной воды 1,33.

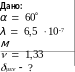
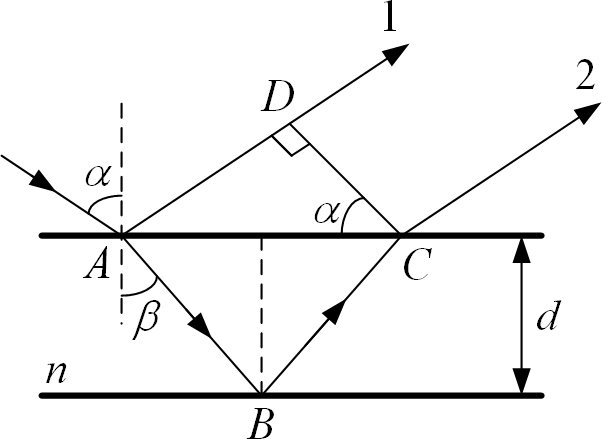Решение. Считаем, что пленка находится в воздухе.

Максимум отражения наблюдается, когда световые волны, отраженные от обеих поверхностей пленки усиливают друг друга.

Условие минимума интерференции имеет вид:   kλ , где k  1, 2,3,...

^{Оптическая разность хода для пучков 1 и 2 равна:   n} ^{AB  BC}  ^{ AD  λ}

2

λ

Слагаемое

2

учитывает, что при отражении пучка 1 от оптически более плотной среды

фаза колебаний электромагнитного поля изменяется на противоположную, т.е. возникает

λ

такое изменение фазы, как при прохождении пути

2

плотной, поэтому изменения фазы не происходит).

d

(пучок 2 отражается от среды менее

Из рисунка видно, что

AB  BC  ,

cos β

AD  AC sinα ,

AC  2dtgβ .

Значит,

AD  2d sinαtgβ .

2dn λ

Тогда,    2d sinαtgβ  .

cos β

2dn

2

λ λ  n 

Значит, kλ 

cos β

• 2d sinαtgβ  ₂  kλ  ₂  2d _{ cos β}  sinαtgβ _ .

По закону преломления имеем:

sinα sin β

 

 n  sinα  nsin β .

^{λ } n nsin² β ^ λ ^ 1  sin² β ^

Значит, kλ  ₂  2d _{ cos β}  _{cos β }  kλ  ₂  2dn_{ cos β } .

   

Из тригонометрии известно, что cos β  .

λ ^ 1  sin² β ^ λ

Значит, kλ   2dn   kλ   2dn .

^{2 } 1  sin² β ^{ 2}

 

λ λ

Значит, kλ   2dn

2

d 

_2k 1_λ

Тогда, .

4

 kλ   2d .

2

_2 1 1_λ _λ

При k  1 толщина пленки минимальная: d_min   .

4

6,5 10^7 _

_{Получаем, d}

  1,6110 ⁷ м ^.

min _{2 2}

₄  _1,33_  sin _60_

7

^Ответ. d_min  1,6110 м ^.

8. На щель шириной 0,2 мм падает нормально параллельный пучок монохроматического света с длиной волны 0,6 мкм. Найти расстояние между первыми дифракционными минимумами на экране, удаленном от щели на 0,5 м.

Решение.

b

x

Условие минимума при дифракции на щели: b sinφ  kλ .

λ

Так как k  1, то bsinφ  λ  sinφ  .

b

φ

x

Из рисунка видно, что tg  .

2l

В виду малости угла φ можно принять, что sinφ  tgφ .

λ x 2lλ

Тогда,

  x  .

b 2l b

2  0,5  6 10^7 _

3

Получаем, x  _{2 104}  310 м .

Ответ. x  3 10^3 м .

9. Естественный свет падает на поверхность диэлектрика под углом полной поляризации. Коэффициент отражения света равен 0,095. Найти степень поляризации преломленного луча.

Дано:

ρ  9,5 10^2

α  α _Б

P  ?

Решение. Если свет падает на границу раздела двух диэлектриков под углом Брюстера, то отражённый луч полностью линейно поляризован перпендикулярно плоскости падания, а преломлённый луч будет поляризован в плоскости падения частично, но максимально по сравнению с другими углами падания. При этом отраженный и преломленный лучи перпендикулярны друг другу.

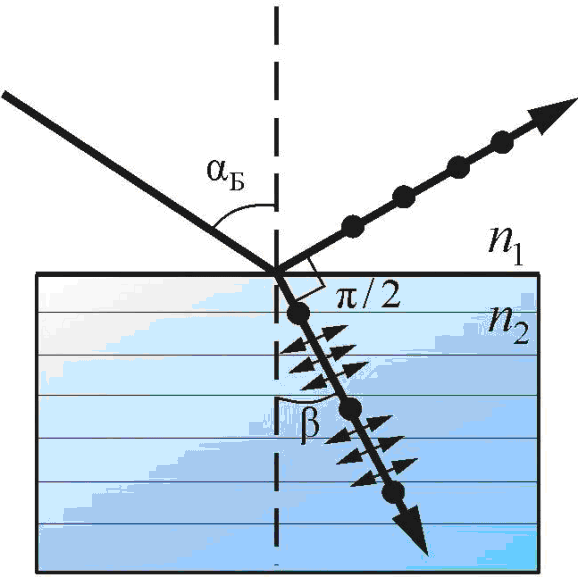
Интенсивность отраженной волны в плоскости перпендикулярной плоскости падения

^{I  sin}^{φ  β}  ^2

^{φ  β} 

равна: I_^  ⁰ _{ } .

_{2 } sin _

Интенсивность отраженной волны в плоскости параллельной плоскости падения равна:

^{I  tg} ^{φ  β}  ^2

^{φ  β} 

I_|^_|  ⁰ _{ } .

_{2 } tg _

Интенсивность преломленной волны в плоскости перпендикулярной плоскости падения

^{I   sin} ^{φ  β}  ^2 ^

равна:

I_^  ^{0 }1  _{ } ^ .

2 _{ } sin _φ  β _{  }

Интенсивность преломленной волны в плоскости параллельной плоскости падения равна:

^{I   tg} ^{φ  β}  ^2 ^

I_|^_|^  ^{0 }1  _{ } ^ .

2 _{ } tg _φ  β _{  }

^{Интенсивность} отраженной волны: I ^  I_|^_|  I_^

Интенсивность преломленной волны:

I ^  I_|^_|^ I_^ .

Так как отраженный и преломленный лучи перпендикулярны друг другу, то имеем:

α _Б  β  90.

I ^sin^{α  β}  ^2 I

I ^{ tg} ^{α  β}  ^2

Значит,

I_^  ⁰ _ ^Б _

^{ 0 sin2} ^{αБ  β}  ^,

^I|^| ^{ 0 } Б ^

 0 .

² _ ^sin ^90 _ ^{2 2} _ ^tg ^90 _

I ^{  sin} ^{α  β}  ^2 ^ I

^{I   0 1 } _ ^Б _ ^{  0 1  sin2} ^{α  β} ^{2  ,}

^ 2 _{ } sin _90_{  } 2 ^{ Б }

 

I ^{  tg} ^{α  β}  ^2 ^ I

_I|^_|^  ^{0 }1  _ ^Б _

_{ } 0 _.

² _

_ tg _90_

_ _ ²

_I  I_|^_|  I_^

Коэффициент отражения падающего света равен: ρ   .

Тогда,

^{I }  I_^

 ^I0 sin² α



₂ Б

• ^β  ^.

I₀ I₀

^I0 sin²

^{α Б  β} 

^sin2 ^α

^{ β}  ₂

Значит,

ρ  ²  ^Б  sin

^{α Б  β}  ^{ 2ρ .}

I₀ 2

Так как α _Б  β  90, то имеем: β  90  α _Б .

Тогда,

_ρ sin² _2α

• 90_

.



Б

2

Степень поляризации преломленного луча равна:

_{P } I_|^_|^ I_^ _.

² I ^ I ^

Значит,

^{I0  I0 1  sin2} ^{α  β} ^{2 }