
Материалы к защите
.pdfВопросы к лабораторной работе
1. Требования к функциям отклика и параметрам.
Изучаемая функция y (29) называется функцией отклика и является математической моделью объекта исследования.
y
y x |
, x |
,..., x ,..., x |
n |
1 |
2 |
i |
.
(1)
Главным требованием к функции отклика является ее способность с необходимой точностью предсказывать направление дальнейших опытов, причем точность предсказания во всех возможных направлениях должна быть одинаковой. Это значит, что в некоторой подобласти, в которую входят и координаты выполненных опытов, предсказанное с помощью модели значение отклика не должно отличаться от фактического больше, чем на некоторую заранее заданную величину. Проверка выполнимости этого условия называется проверкой адекватности модели.
Выходной параметр процесса должен быть: 1) задан количественно, т.е. иметь численное значение; 2) однозначен, т.е. заданному набору значений факторов должно соответствовать одно с точностью до ошибки эксперимента значение выходного параметра; 3) эффективен с точки зрения достижения цели и в статистическом смысле; 4) универсален (наиболее хороши здесь обобщенные параметры такие, например, как рассмотренные в разделе теории безразмерные комплексы); 5) прост и иметь ясный физический смысл; 6) действителен для всех различных состояний.
Факторы должны быть управляемыми, т.е. чтобы можно было, задав нужное их значение, поддерживать его на постоянном уровне в течение всего эксперимента. Точность замера факторов необходима возможно более высокая. Вся совокупность факторов должна быть совместима, а сами факторы – независимы, т.е. необходимо выполнение условия установить фактор на любом уровне вне зависимости от уровней других факторов. Требование некоррелированности не означает, что между значениями факторов нет никакой связи. Достаточно, чтобы эта связь не была линейной.
2.Диапазон варьирования.
Одним из самых ответственных моментов этого этапа является правильный выбор интервалов варьирования факторами xi . При слишком малом значении xi функция отклика может очень слабо
реагировать на изменение фактора
xi
в пределах от нижнего до верхнего уровней. Выбор слишком большого
интервала варьирования также приводит к отрицательным результатам.
Что же может служить исходным для правильного выбора
xi
? Для начала это априорные сведения о
степени влияния каждого фактора на рассматриваемый процесс. Они могут быть получены из уже проведенных аналогичных исследований, из предварительных однофакторных экспериментов или же из соответствующей научной литературы. В крайнем случае интервалы варьирования выбираются интуитивно. Тем более, что сам метод ПФЭ после его реализации дает информацию о том, насколько правильно выбраныxi и как их нужно изменить, если они были выбраны неверно.
На интервалы варьирования накладываются естественные ограничения. Они не могут быть меньше ошибки, с которой фиксируются уровни факторов; не могут быть настолько большими, чтобы верхний и нижний уровни оказались за пределами области существования. В задачах оптимизации для первой серии опытов выбирается такая подобласть факторного пространства, чтобы обеспечить возможность шагового движения к экстремуму. В задачах интерполяции интервалы охватывают всю исследуемую область.
Выбор интервалов варьирования – трудная неформализованная задача, которая решается по результатам анализа точности фиксации уровней факторов, сведений о кривизне поверхности отклика и диапазоне изменения параметра выхода. На предварительном этапе исследования можно рекомендовать следующие границы варьирования: широкий интервал – он составляет более 30% от области определения фактора; средний – от 10 до 30%; узкий – менее 10% от области определения. Однако в каждой конкретной задаче приходится специально определять эти понятия градаций.

3. Центр эксперимента.
Метод полного факторного эксперимента (ПФЭ) дает возможность получить математическое описание исследуемого объекта или процесса в некоторой локальной области факторного пространства, лежащей в
окрестности точки с координатами
x |
, x |
,..., x |
,..., x |
01 |
02 |
0i |
0n |
. Эта точка называется центром эксперимента. ПФЭ
тем эффективнее, чем большее число независимых переменных принимается во внимание, однако количество опытов при этом растет.
4. С какой целью нормируют факторы?
Второй этап метода ПФЭ включает преобразование факторов из натурального масштаба в безразмерный, что облегчает в дальнейшем математическую обработку результатов эксперимента. Для этого можно воспользоваться формулой
|
|
|
|
|
x x |
|
|
|
|
|
|
X |
|
|
i |
0i |
, |
i 1, 2,..., n |
, (2) |
|
|
i |
|
x |
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
где |
Xi |
- кодировочное значение фактора; xi |
|
- |
натуральное значение фактор; |
||||
основного уровня; xi - интервал варьирования; |
i 1, 2,..., n - номер фактора. |
||||||||
При методе ПФЭ функцию отклика обычно ищут в виде
x0i
- натуральное значение
y b |
b x |
b x |
... b x b |
x x ... b |
|||
0 |
1 1 |
2 2 |
n n |
12 |
1 2 |
|
n |
Причем в ряде случаем достаточно лишь линейной зависимости |
y |
||||||
|
|||||||
|
|
y b0 |
b1x1 b2 x2 |
... bn xn |
(4) |
||
1,n |
x |
x |
|
|
n 1 |
n |
|
от |
xi |
|
|
(3)
Основанием для такого упрощения может служить следующее положение. Из курса математического
анализа известно, что достаточно «хорошую» функцию |
y |
от многих переменных в окрестности некоторой |
|
точки, например, точки с координатами
x |
, x |
,..., |
01 |
02 |
|
x0n
, можно разложить в ряд Тейлора. Если же эта
окрестность достаточно мала, то линейная часть разложения ряда Тейлора будет вполне удовлетворительно описывать поведение этой функции. Учитывая сказанное, легко понять, почему слишком большой интервал варьирования может привести к неправильному результату.
5.Что означает, когда эксперимент воспроизводим?
Проверка воспроизводимости результатов эксперимента
Прежде всего необходимо убедиться в том, что опыты воспроизводимы, т.е. статистически достоверны. Для этой цели в каждой серии параллельных экспериментов, проведенных в одинаковых условиях, определяются дисперсии:
|
1 |
|
|
y ji |
y j |
2 |
|
S 2j |
|
i 1 |
(5) |
||||
|
|
|
|||||
1 |
|
||||||
Для проверки воспроизводимости опытов находят отношение наибольшей из дисперсий к сумме всех |
|||||||
остальных: |
|
|
|
|
|
|
|
G |
|
|
|
S 2j |
max |
(6) |
|
|
|
||||
p |
|
|
|
|||
|
|
|
S 2j |
|||
|
|
|
|
j |
|
|
Величина Gp называется расчетным значением критерия Кохрена. Она сравнивается с табличным |
||||||
значением GT (см. приложение 1). Для определения GT |
требуется знать доверительную вероятность P и число |
|||||

степеней свободы fc , связанные с каждой из дисперсий |
|
S |
2 |
|
|
|
||
|
j . Обычно принимают надежность опытов |
|||||||
|
|
|||||||
, а |
fc |
рассчитывают по формуле |
|
|
|
|
|
|
|
|
fc |
1. |
|
|
|
||
|
|
Если выполняется условие |
|
|
|
|
|
|
|
|
Gp |
GT , |
|
|
|
||
|
|
то опыты считаются воспроизводимыми, а оценки дисперсий |
S |
2 |
- однородными. |
|||
|
|
j |
||||||
|
|
|
||||||
P 0.95
Если опыты невоспроизводимы, то необходимо выявить источники нестабильности эксперимента, ликвидировать их и повторить эксперимент снова. В том случае, когда нельзя достигнуть воспроизводимости эксперимента, математические методы планирования применять нельзя. Возможны такие варианты, когда не будет воспроизводиться серия параллельных опытов, которые, скажем, имеют в результате наибольшую дисперсию. Это может произойти в случае «выброса» эксперимента, например, в результате ошибки показаний прибора. Тогда можно заменить этот опыт повторным или отбросить указанное значение, пересчитав соответствующим образом дисперсию.
6. Проверка воспроизводимости результатов эксперимента
Прежде всего необходимо убедиться в том, что опыты воспроизводимы, т.е. статистически достоверны. Для этой цели в каждой серии параллельных экспериментов, проведенных в одинаковых условиях, определяются дисперсии:
|
|
1 |
|
|
2 |
S j |
|
y ji |
y j |
||
2 |
|
|
|
|
|
|
|
1 |
i 1 |
|
|
|
|
|
|
|
(7)
Для проверки воспроизводимости опытов находят отношение наибольшей из дисперсий к сумме всех остальных:
|
|
|
|
S |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
j |
|
max |
(8) |
|
|
|
|
|
||||
|
p |
S j |
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
j |
|
|
|
|
Величина Gp |
называется расчетным значением критерия Кохрена. Она сравнивается с табличным значением GT |
|||||||
(см. приложение 1). Для определения GT требуется знать доверительную вероятность P и число степеней свободы fc ,
связанные с каждой из дисперсий S 2j . Обычно принимают надежность опытов P 0.95 , а fc рассчитывают по формуле
fc 1. |
|
||
Если выполняется условие |
|
|
|
Gp GT |
, |
|
|
то опыты считаются воспроизводимым, а оценки дисперсий |
S |
2 |
|
j |
|||
|
|||
- однородными.
Если опыты невоспроизводимы, то необходимо выявить источники нестабильности эксперимента, ликвидировать их и повторить эксперимент снова. В том случае, когда нельзя достигнуть воспроизводимости эксперимента, математические методы планирования применять нельзя. Возможны такие варианты, когда не будет воспроизводиться серия параллельных опытов, которые, скажем, имеют в результате наибольшую дисперсию. Это может произойти в случае «выброса» эксперимента, например, в результате ошибки показаний прибора. Тогда можно заменить этот опыт повторным или отбросить указанное значение, пересчитав соответствующим образом дисперсию.

7. Физический смысл b0 и b12
При методе ПФЭ функцию отклика обычно ищут в виде
y b |
b x |
b x |
... b x |
b |
x x |
... b |
x |
x |
0 |
1 1 |
2 2 |
n n |
12 |
1 2 |
n 1,n |
n 1 |
n |
Причем в ряде случаем достаточно лишь линейной зависимости |
y |
от |
x |
, т.е. |
|
|
|
i |
|
y b0 b1x1 b2 x2 ... bn xn |
(10) |
|||
(9)
Основанием для такого упрощения может служить следующее положение. Из курса математического анализа
известно, что достаточно «хорошую» функцию |
y |
от многих переменных в окрестности некоторой точки, например, |
|
точки с координатами x01 , x02 ,..., x0n , можно разложить в ряд Тейлора. Если же эта окрестность достаточно мала, то линейная часть разложения ряда Тейлора будет вполне удовлетворительно описывать поведение этой функции.
Вычисление коэффициентов уравнения регрессии
Коэффициенты уравнения (31) вычисляются по формулам:
|
|
|
|
|
1 |
N |
|
|
|
|
|
|
|
|
|
b0 |
|
y j |
(11) |
|
|
|
|||
|
|
|
N |
|
|
|
||||||
|
|
|
|
|
j 1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
N |
|
|
|
|
|
|
|
|
bi |
|
xij |
y j |
(12) |
|
|
|
||
|
|
|
N |
|
|
|
||||||
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
N |
|
|
|
|
|
|
|
|
|
bim |
|
xij xjm y j (13) |
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
N |
j 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
где |
N |
- количество экспериментов (параллельные опыты не считаются). Для табл. 3 |
N 4 |
, для табл. 4 |
N 8 . |
|||||||
Заключительной процедурой является статистическая проверка результатов проведенной серии экспериментов.
9. Проверка на значимость коэффициентов bi и bim .
Некоторые из коэффициентов уравнения (31) могут оказаться пренебрежимо малыми – статистически незначимыми. Чтобы установить это, необходимо прежде всего вычислить оценку дисперсии единичного измерения:
|
|
|
|
|
|
|
|
|
1 |
N |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
(14) |
|
|
|
|
|
|
|
|
|
Sy |
N |
S j |
|
||
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
2 |
2 |
1 |
|
2 |
|
|
|
|
|
|
Тогда дисперсия среднего |
y равна Sy |
|
Sy |
(15) |
|
|
|
|
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sy |
|
2 |
|
|
|
|
|
|
|
и ошибка эксперимента составляет |
Sy |
(16) |
|
|
|
|
|
|||||
Принято считать, что коэффициент регрессии bi значим, если выполняется условие tp tT , |
i 0,1,...k (17) |
|||||||||||
|
i |
где tT |
- табличное значение критерия Стьюдента (см. приложение 2). |
Расчетное значение t pi определяется из формулы
t |
|
|
|
b |
|
|
i |
||
|
|
|
|
|
|
p |
S |
|
N |
|
i |
|
||
|
|
|
|
|
|
|
|
g |
|
(18)
Для нахождения tT по таблицам необходимо знать доверительную вероятность (надежность) P и число степеней свободы fc . Первая принимается равной 0,95, а fc вычисляется следующим способом:
fc N 1 .
В случае, если условие (42) не выполняется для какого-либо коэффициента bi , то соответствующий фактор можно исключить из уравнения (31).

10 Что значит когда уравнение регрессии адекватно?
Получив в результате проведения и обработки серии опытов уравнение (31), следует проверить его адекватность (эквивалентность) результатам эксперимента с помощью критерия Фишера, представляющего собой отношение
где
где
|
|
|
|
|
|
|
|
|
|
|
|
S |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
F |
|
ag |
(19) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
p |
|
S |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S |
2 |
- оценка дисперсий адекватности, которая для уравнения (32) находится по формуле |
|||||||||||||||
ag |
|||||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
N |
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
Sag2 |
|
y j2 |
|
N bi2 |
(20) |
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
fc j 1 |
|
|
|
i 0 |
|
|||
к |
- число факторов, а |
f |
c |
N |
|
к 1 |
- число степеней свободы при оценке дисперсии адекватности. |
||||||||||
|
|
|
|||||||||||||||
Уравнение (32) считается адекватным результатам экспериментов и может быть использовано, если выполнено условие
где
FT
Fp FT (21)
- табличное значение критерия Фишера (см. приложение 3).
Для определения значения
FT
по таблице необходимо знать число степеней свободы, связанных с числителем и
знаменателем выражения (44) и доверительную вероятность P , которая принимается равной 0,95.
11. Алгоритм действий, если уравнение неадекватное.

Вопросы к домашнему заданию
1. Почему температура поверхности зубчатых передач в постоянно сцепленных парах не совпадает с температурой смазки в объеме.

2. Откуда появляется температура вспышки, что это

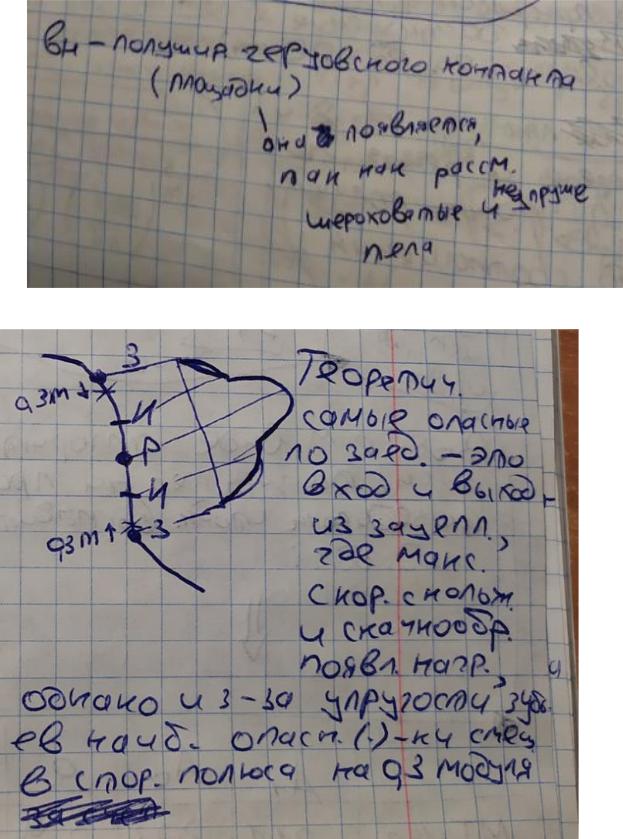
3. Откуда появляется полуширина Герцевского контакта?
5 Какие точки наиболее опасны по износу и заеданию?

6 Что такое равновесная шероховатость?
Исходная шероховатость состоит из совокупности различных по величине и геометрическому очертанию неровностей; в процессе приработки эти неровности будут подвержены воздействию различных касательных и нормальных напряжений. Значительным интенсивным воздействиям будут подвержены наиболее высокие неровности, которые за счет больших напряжений будут либо срезаться, либо пластически деформироваться. Наиболее пологие неровности также будут испытывать интенсивное воздействие за счет большой адгезии, что приведет к значительному изменению их геометрического очертания. Поэтому в ансамбле неровностей, имеющих различную высоту и радиус закругления, в более благоприятных условиях окажутся промежуточные по своим размерам неровности. Эти неровности будут превалирующими на приработанной поверхности. Для таких приработанных поверхностей сила трения будет иметь минимальное значение. Таким образом, равновесная шероховатость для установившегося процесса соответствует минимальному значению сил трения при прочих равных условиях.
То есть равновесная шероховатость наступает спустя 15-20 часов, то есть когда заканчивается приработка и она является главным критерием конца приработки.
7 Как влияет температура на интенсивность изнашивания?
Чем выше температура, тем выше интенсивность изнашивания и круче располагается семейство кривых
