2. Задача о покрытии

2.1 Условие задачи

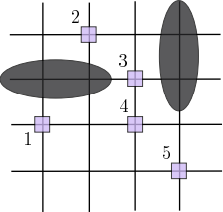
В районе города, схема которого изображена на рисунке 1, рассматривается возможность размещения пожарных участков (возможные точки размещения обозначены номерами, линии соответствуют дорогам, а закрашенные эллипсы - природным объектам). Стоимость размещения участка в каждой из точек указана в табл. 1).

Требуется найти такое размещение участков, при котором стоимость была бы минимальна, но (манхэттенское) расстояние от каждого перекрестка до ближайшего участка было не более 3.

Стоимость размещения участка

Расположение	Стоимость, д.е.
1	100
2	300
3	300
4	250
5	100

2.2 Формализация задачи

Нам дана задача, которая относится к линейному программированию, а если быть точнее, то это «Задача о покрытии».

Функция цели должна стремиться к минимуму, так как необходимо свести затраты к наименьшему значению:

𝐹 = 100𝑥₁ + 300𝑥₂ + 300𝑥₃ + 250𝑥₄ + 100𝑥₅ → 𝑚𝑖𝑛

Где 𝑥_𝑖 - переменные, принимающие значение только либо 0, либо 1, другими словами, булевы переменные. Соответственно, если участок размещен, то значение 1, в противном случае 0.

Для того чтобы обозначить ограничения на схеме города пронумеруем перекрестки (см. рисунок 2).

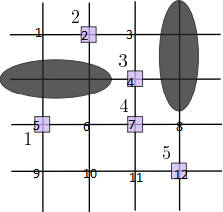
Теперь рассмотрим все ограничения, всего их будет 12, так как мы имеем 12 перекрёстков:

1. 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 0𝑥₁ + 0𝑥₁ ≥ 1

2. 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ + 0𝑥₁ ≥ 1

3. 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ + 0𝑥₁ ≥ 1

4. 1𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ ≥ 1

5. 1𝑥₁ + 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 0𝑥₁ ≥ 1

6. 1𝑥₁ + 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ ≥ 1

7. 1𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ ≥ 1

8. 1𝑥₁ + 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ ≥ 1

9. 1𝑥₁ + 0𝑥₁ + 0𝑥₁ + 1𝑥₁ + 1𝑥₁ ≥ 1

10.1𝑥₁ + 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ ≥ 1

11.1𝑥₁ + 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ ≥ 1

12.0𝑥₁ + 0𝑥₁ + 1𝑥₁ + 1𝑥₁ + 1𝑥₁ ≥ 1

Рассмотрим, как получились ограничения на примере первого. В данном случае рассматривается первый перекресток, от него мы отсчитываем манхэттенское расстояние до каждого пожарного участка, то есть идем от перекрестка к перекрестку по дороге и считаем их количество, если оно не превышает 3, то перекресток может обслуживаться, соответственно выбираем 1, иначе ставим 0. Видим, что в первом ограничении, расстояние от перекрестка до 1-ого участка 6, ставим 0; до 2-ого участка 1, ставим 1; до 3-его участка 3, ставим 1; до 4-ого участка 4, ставим 0; до 5-ого участка 6, ставим 0. Кроме того, знак неравенства показывает, что перекресток может обслуживаться 1 и более участками.

2.3 Решение задачи

Код выглядит следующим образом:

import numpy as np

from scipy.optimize import linprog

 

# Коэффициенты функции цели

c = np.array([100, 300, 300, 250, 100])

 

A = np.array([

[0, 1, 1, 0, 0],

[0, 1, 1, 1, 0],

[0, 1, 1, 1, 0],

[1, 1, 1, 1, 1],

[1, 0, 1, 1, 0],

[1, 0, 1, 1, 1],

[1, 1, 1, 1, 1],

[1, 0, 1, 1, 1],

[1, 0, 0, 1, 1],

[1, 0, 1, 1, 1],

[1, 0, 1, 1, 1],

[0, 0, 1, 1, 1]

])

# Ограничения (правая часть)

b = np.ones(12)

 

# Указание, что переменные должны быть бинарными

bounds = [(0, 1) for _ in range(5)]

 

 

# Решение задачи

res = linprog(c, A_ub=-A, b_ub=-b, bounds=bounds, method='highs')

 

# Преобразуем значения к бинарным (0 или 1) и к целым числам

x_binary = np.round(res.x).astype(int)

 

print(f"Минимальная стоимость: {res.fun}")

print(f"Размещение участков: {x_binary}")

В данном коде c - коэффициенты функции цели, a - левая часть матрицы ограничений, b - правая часть матрицы ограничений.

Результат работы программы:

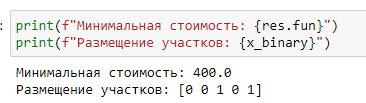
По нему мы можем сказать, что минимальная стоимость размещения пожарных участков будет равна 400, при условии, что участки будут находиться на 3 и 5 местах.