МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра Информационных систем

ПРАКТИЧЕСКАЯ РАБОТА

по дисциплине «Теория принятия решений»

Тема: Применение методов линейного и динамического программирования для решения практических задач (по вариантам)

Вариант: 109

Студентка гр.
Преподаватель		Пономарёв А.В.

Санкт-Петербург 2024

ОГЛАВЛЕНИЕ

Оглавлени

МИНОБРНАУКИ РОССИИ 1

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) 1

ПРАКТИЧЕСКАЯ РАБОТА 1

Тема: Применение методов линейного и динамического программирования для решения практических задач (по вариантам) 1

ОГЛАВЛЕНИЕ 2

ВВЕДЕНИЕ 4

1. Задача о найме персонала 5

1.1 Условие задачи 5

1.2 Формализация задачи 6

Ограничения: 7

1.3 Решение задачи 10

2. Задача о покрытии 15

2.1 Условие задачи 15

2.2 Формализация задачи 16

2.3 Решение задачи 19

3. Задача о сенсоре 20

3.1. Условие задачи 20

3.2. Формализация задачи 21

3.3. Решение задачи 23

ЗАКЛЮЧЕНИЕ 28

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 29

ВВЕДЕНИЕ 3

1. Задача о найме персонала 4

1.1 Условие задачи 4

1.2 Формализация задачи 5

1.3 Решение задачи 8

2. Задача о покрытии 13

2.1 Условие задачи 13

2.2 Формализация задачи 14

2.3 Решение задачи 16

3. Задача о сенсоре 17

3.1. Условие задачи 17

3.2. Формализация задачи 18

3.3. Решение задачи 20

ЗАКЛЮЧЕНИЕ 25

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 26

Введение

Целью практической работы является нахождение оптимального решения задачи линейного программирования. Для выполнения работы использовался язык программирования Python.

1. Задача о найме персонала

1. Условие задачи

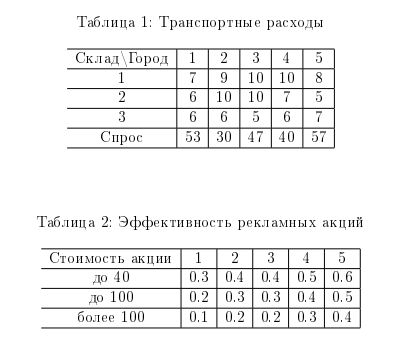
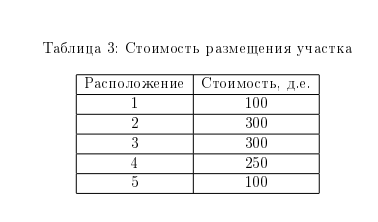
Запасы товара на трех складах торговой компании, составляют 125, 136, и 143. Компания имеет пункты реализации товара в пяти населенных пунктах, причем средние транспортные затраты на перевозку единицы товара из складов в населенные пункты, а также спрос на товар в каждом из пунктов указаны в табл.1. Для стимуляции спроса торговая компания может провести рекламную акцию в каждом из пунктов. Потенциальный эффект от рекламной акции (увеличение спроса на единицу стоимости рекламной акции) зависит от бюджета рекламной акции. Параметры зависимости различны для городов и сведены в табл. 2. Следует обратить внимание, что эффект характеризуется убывающей отдачей (что в определенной степени моделирует насыщение рынка). Так, например, при бюджете рекламной акции 120, увеличение спроса в первом городе будет вычисляться следующим образом: 0.5*40 + 0.4*60 + 0.3*(120 - 40 - 60). Требуется:

1. Определить минимальные издержки на реализацию всего товара. 2. Выявить населенные пункты, требующие максимальный и минимальный рекламный бюджет.

3. Провести анализ чувствительности оптимальной стратегии к стоимости перевозок между складом 2 и населенным пунктом 3.

1.2 Формализация задачи

𝑥_𝑖,𝑗, 𝑖 = номер склада ⁽1 … 3⁾; 𝑗 = номер населенного пункта(1 … 5) – количество товара перевезенного из склада i в пункт j.

𝑐_𝑖,𝑗, 𝑖 = номер склада ⁽1 … 3⁾; 𝑗 = номер населенного пункта(1 … 5) – стоимость перевозки из склада i в пункт j.

𝑦_𝑖 , 𝑖 = номер населенного пункта ⁽1 … 5⁾ – количество вложенных в рекламу в i-ый населенный пункт денег.

1

Целевая функция, учитывающая расход денег на рекламу и транспортировку:

𝑖=1

𝑓⁽𝑥⁾ = ^∑3

5

∑

𝑗=1

𝑐_𝑖,𝑗 ∙ 𝑥_𝑖,𝑗 + ^∑5 𝑦_𝑖 → 𝑚𝑖𝑛.

Ограничения:

Так как нужно продать весь товар на складах, то задаем ограничение в виде равенств:

𝑥_1,1 + 𝑥_1,2 + … + 𝑥_1,5 = 125

𝑥_2,1 + 𝑥_2,2 + … + 𝑥_2,5 = 136

𝑥_3,1 + 𝑥_3,2 + … + 𝑥_3,5 = 143

Т.к. предложение не должно превышать спрос, который зависит от количества вложенных в рекламу денег построим систему неравенств:

(1) 𝑥_1,𝑖 + 𝑥_2,𝑖 + 𝑥_3,𝑖 ≤ ℎ_𝑖 + 𝑓_𝑖⁽𝑦_𝑖⁾, 𝑖 = ⁽1 … 5⁾ – номер населенного пункта

ℎ_𝑖 – i-ый эл-т в таблице 1. (спрос в i-ом населенном пункте при отсутствии рекламы)

𝑓_𝑖⁽𝑦_𝑖⁾ − функция увеличения спроса в i-ом населенном пункте от суммы вложения в рекламу в этот город 𝑦_𝑖 . Данная функция имеет различный вид, в зависимости от диапазона значений аргумента, т.е. 𝑓_𝑖⁽𝑦_𝑖⁾ − кусочно-линейная функция имеющая следующий вид на 3-ёх интервалах:

(2) 𝑓_𝑖⁽𝑦_𝑖⁾ = 𝑘_1,𝑖 ∙ 𝑦_𝑖, 𝑦_𝑖 ∈ ⁽0; 40^]

(3) 𝑓_𝑖⁽𝑦_𝑖⁾ = 𝑘_1,𝑖 ∙ 40 + 𝑘_2,𝑖 ∙ (𝑦_𝑖 − 40), 𝑦_𝑖 ∈ ⁽40; 100^]

(4)𝑓_𝑖⁽𝑦_𝑖⁾ = 𝑘_1,𝑖 ∙ 40 + 𝑘_2,𝑖 ∙ 60 + 𝑘_3,𝑖 ∙ (𝑦_𝑖 − 100), 𝑦_𝑖 ∈ ⁽100; ∞^],

где 𝑘_𝑙,𝑖 – коэффициент зависимости спроса от вложенных в рекламу денег на диапазоне вложенных в рекламу денег в количестве лежащем в 1-ом из 3ёх диапазонов l = (1…3).

Введем дополнительную переменную 𝑔_𝑖 = 𝑓_𝑖⁽𝑦_𝑖⁾. Тогда мы сможем избавиться от кусочно-линейной функции следующим образом:

(1) , (2), (3), (4)



𝑖 = ⁽1 … 5⁾

^𝑥1,𝑖 ^{+ 𝑥}2,𝑖 ^{+ 𝑥}3,𝑖 ^{≤ ℎ}𝑖 ^{+ 𝑔}𝑖

𝑔_𝑖 ≤ 𝑘_1,𝑖 ∙ 𝑦_𝑖

𝑔_𝑖 ≤ 𝑘_1,𝑖 ∙ 40 + 𝑘_2,𝑖 ∙ (𝑦_𝑖 − 40)

𝑔_𝑖 ≤ 𝑘_1,𝑖 ∙ 40 + 𝑘_2,𝑖 ∙ 60 + 𝑘_3,𝑖 ∙ (𝑦_𝑖 − 100)

 (соединим неравенства (a < b < c  a < c), раскроем скобки и перенесем все переменные в левые части неравенств, а свободные члены – в правые)

𝑖 = ⁽1 … 5⁾

^𝑥1,𝑖 ^{+ 𝑥}2,𝑖 ^{+ 𝑥}3,𝑖 ^{− 𝑘}1,𝑖 ^{∙ 𝑦}𝑖 ^{≤ ℎ}𝑖

𝑥_1,𝑖 + 𝑥_2,𝑖 + 𝑥_3,𝑖 − 𝑘_2,𝑖 ∙ 𝑦_𝑖 ≤ ℎ_𝑖 + 40 ∙ (𝑘_1,𝑖 − 𝑘_2,𝑖)

𝑥_1,𝑖 + 𝑥_2,𝑖 + 𝑥_3,𝑖 − 𝑘_3,𝑖 ∙ 𝑦_𝑖 ≤ ℎ_𝑖 + 𝑘_1,𝑖 ∙ 40 + 𝑘_2,𝑖 ∙ 60 − 100 ∙ 𝑘_3,𝑖

Кроме того, как число перевозимого товара, так и число выделенных денег не могут быть отрицательными:

𝑥_𝑖,𝑗 ≥ 0, 𝑦_𝑖 ≥ 0

Это задача линейного программирования, так как целевая функция и ограничения задачи имеют линейную форму; не имеется каких-либо управлений и промежуточных состояний.